ESERCIZIO B.1 a) gli autovalori della matrice dei coefficienti sono
 . La matrice della nuova base
. La matrice della nuova base
con per colonne un autovettore di autovalore  , la parte immaginaria e la parte reale di un autovettore di autovalore
, la parte immaginaria e la parte reale di un autovettore di autovalore  (in questo ordine), definisce la matrice del cambiamento di coordinate
(in questo ordine), definisce la matrice del cambiamento di coordinate
per cui la matrice che esprime il flusso integrale è:
b) Le condizioni iniziali che hanno l'origine come 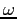 -limite sono quelle nello spazio vettoriale reale generato dai due autospazi degli autovalori complessi, che hanno parte reale negativa; in pratica, quelli con prima componente 0, cioè quelli combinazione lineare di
-limite sono quelle nello spazio vettoriale reale generato dai due autospazi degli autovalori complessi, che hanno parte reale negativa; in pratica, quelli con prima componente 0, cioè quelli combinazione lineare di 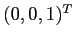 e di
e di 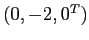 . Le condizioni iniziali che hanno l'origine come
. Le condizioni iniziali che hanno l'origine come 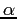 -limite sono quelle nell'autospazio dell'autovalore reale positivo, cioè i multipli di
-limite sono quelle nell'autospazio dell'autovalore reale positivo, cioè i multipli di 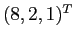 .
.
ESERCIZIO B.2 Si noti che l'integrale dell'energia è:
con la costante scelta per avere 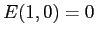 .
.
Figura C.10:
b) Energia potenziale e curve di livello dell'energia.
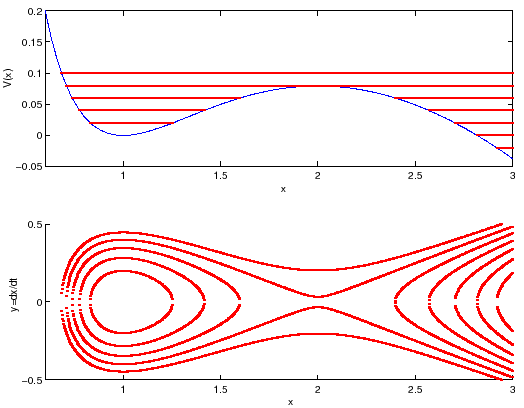 |
a,b) I punti di equlibrio sono 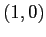 con linearizzato di tipo centro (con autovalori
con linearizzato di tipo centro (con autovalori 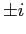 ), che è stabile perché corrisponde ad un minimo dell'energia potenziale, e
), che è stabile perché corrisponde ad un minimo dell'energia potenziale, e 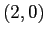 di tipo sella (linearizzato con autovalori
di tipo sella (linearizzato con autovalori 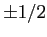 ), che è instabile come ogni sella nonlineare (per il teorema di esistenza delle curve eccezionali). Qualitativamente, le separatrici formano un fiocco che si incrocia nel punto
), che è instabile come ogni sella nonlineare (per il teorema di esistenza delle curve eccezionali). Qualitativamente, le separatrici formano un fiocco che si incrocia nel punto 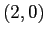 e si richiude a sinistra del punto
e si richiude a sinistra del punto 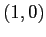 .
.
c) Usare l'insieme invariante
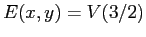 (componente connessa per
(componente connessa per 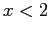 ) per mostrare che la soluzione è periodica, quindi coincide con il suo
) per mostrare che la soluzione è periodica, quindi coincide con il suo 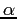 -limite e anche con il suo
-limite e anche con il suo 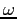 -limite.
-limite.
Figura C.11:
e) Le separatrici nel caso con dissipazione.
 |
d,e) I punti di equilibrio sono gli stessi, con 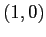 che è diventato un pozzo (linearizzato di tipo fuoco, autovalori complessi con parte reale
che è diventato un pozzo (linearizzato di tipo fuoco, autovalori complessi con parte reale 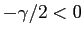 ), mentre
), mentre 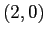 resta una sella nonlineare, gli autospazi ruotati in verso antiorario rispetto al caso con
resta una sella nonlineare, gli autospazi ruotati in verso antiorario rispetto al caso con 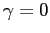 . Qualitativamente la separatrice stabile racchiude il bacino di attrazione di
. Qualitativamente la separatrice stabile racchiude il bacino di attrazione di 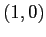 , indicato con A, la separatrice instabile ha un lato che appartiene al bacino di
, indicato con A, la separatrice instabile ha un lato che appartiene al bacino di 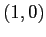 e uno che va all'infinito, come tutte le orbite contenute nell'insieme indicato con B.
e uno che va all'infinito, come tutte le orbite contenute nell'insieme indicato con B.
f) La funzione 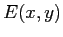 è funzione di Lyapounov per il punto di equlibrio
è funzione di Lyapounov per il punto di equlibrio 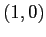 , perciò basta provare che la regione positivamente invariante
, perciò basta provare che la regione positivamente invariante
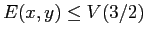 non contiene nessun altro punto critico (infatti
non contiene nessun altro punto critico (infatti
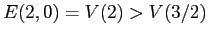 ), mentre al di fuori dei punti critici la funzione di Lyapounov decresce strettamente su ogni orbita. Quindi la regione invariante, ivi compreso il punto
), mentre al di fuori dei punti critici la funzione di Lyapounov decresce strettamente su ogni orbita. Quindi la regione invariante, ivi compreso il punto 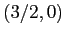 , appartiene al bacino di attrazione di
, appartiene al bacino di attrazione di 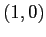 .
.
g) La separatrice stabile, che fa da bordo al bacino di attrazione, parte da 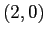 verso le
verso le 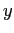 positive con tangente parallela all'autospazio del linearizzato che ha direzione
positive con tangente parallela all'autospazio del linearizzato che ha direzione
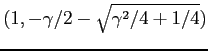 , cioè verso l'alto a sinistra, e poi piega verso il basso, quindi passa a sinistra del punto
, cioè verso l'alto a sinistra, e poi piega verso il basso, quindi passa a sinistra del punto 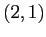 . Quindi
. Quindi 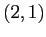 appartiene all'insieme B della figura C.11; l'orbita con quelle condizioni iniziali non può avere per
appartiene all'insieme B della figura C.11; l'orbita con quelle condizioni iniziali non può avere per 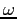 -limite nessun punto singolare, e nessuna orbita periodica perché non ce ne sono (cosa farebbe la funzione
-limite nessun punto singolare, e nessuna orbita periodica perché non ce ne sono (cosa farebbe la funzione 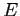 su di un orbita periodica?), quindi deve per forza uscire da ogni compatto. Per mostrare che ha proprio limite infinito si può usare il fatto che la tangente ha un limite definito, che è orizzontale.
su di un orbita periodica?), quindi deve per forza uscire da ogni compatto. Per mostrare che ha proprio limite infinito si può usare il fatto che la tangente ha un limite definito, che è orizzontale.
ESERCIZIO B.3 a) L'equazione alle differenze finite del secondo ordine è:
che si trasforma nel sistema dinamico discreto:
b) Se
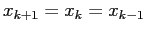 allora
allora 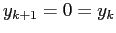 . Perciò l'equazione
. Perciò l'equazione 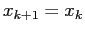 si riduce a
si riduce a
quindi ci sono tre punti fissi esattamente dove il sistema dinamico continuo ha i suoi tre punti di equilibrio.
c) La Jacobiana
ha determinante 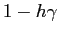 e traccia
e traccia
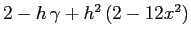 .
.
La linearizzazione in 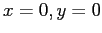 ha traccia
ha traccia
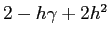 , e quindi il polinomio caratteristico
, e quindi il polinomio caratteristico
è tale che
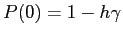 è compreso tra 0 e 1 (almeno per
è compreso tra 0 e 1 (almeno per 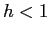 ) e
) e 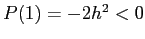 , per cui ha una radice reale tra
, per cui ha una radice reale tra 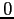 e
e 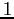 e un altra maggiore di
e un altra maggiore di 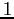 .
.
d) In
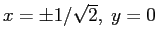 la linearizzazione ha traccia
la linearizzazione ha traccia
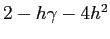 e quindi il polinomio caratteristico è tale che
e quindi il polinomio caratteristico è tale che
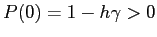 e
e 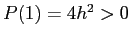 , perciò ha o due autovalori reali tra
, perciò ha o due autovalori reali tra 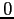 e
e 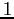 oppure due autovalori complessi di modulo
oppure due autovalori complessi di modulo
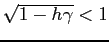 . Perciò i due punti fissi
. Perciò i due punti fissi
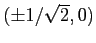 sono dei pozzi nonlineari.
sono dei pozzi nonlineari.
ESERCIZIO B.4 a) La parametrizzazione
porta all'energia cinetica e all'energia potenziale
Quindi 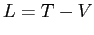 e l'equazione di Lagrange è
e l'equazione di Lagrange è
b) La trasformazione di Legendre
porta alla hamiltoniana
e le equazioni di Hamilton sono
c) I punti di equilibrio sono per
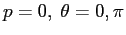 (modulo
(modulo 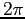 ), e se esiste una soluzione diversa di
), e se esiste una soluzione diversa di
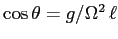 , cioè per
, cioè per
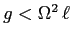 , anche
, anche
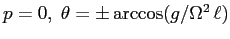 . La matrice jacobiana
. La matrice jacobiana
ha sempre traccia nulla, e determinante
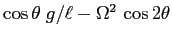 . In
. In
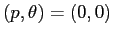 il determinante è
il determinante è
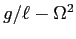 e si ha un punto stabile (per il teorema di stabilità del minimo) se
e si ha un punto stabile (per il teorema di stabilità del minimo) se
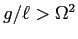 , un punto di sella nonlineare per
, un punto di sella nonlineare per
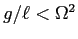 .
.
Per
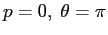 il determinante del linearizzato è
il determinante del linearizzato è
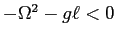 e quindi c'è sempre una sella nonlineare. Nel caso
e quindi c'è sempre una sella nonlineare. Nel caso
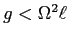 i due punti
i due punti
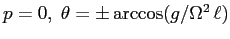 il determinante è
il determinante è
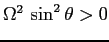 e ci sono due punti stabili.
e ci sono due punti stabili.
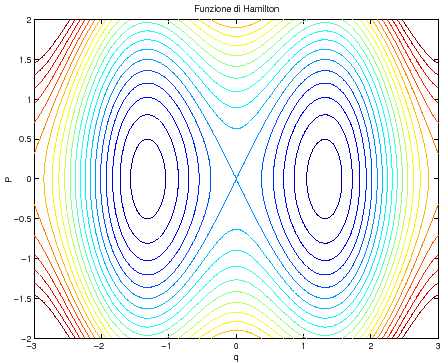
Figura C.12:
d) Curve di livello della funzione di Hamilton.
 |
e)  mentre
mentre 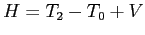 dove
dove 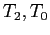 sono le parti di
sono le parti di 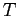 omogenee in
omogenee in 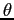 di grado 2 e 0 rispettivamente; quindi
di grado 2 e 0 rispettivamente; quindi 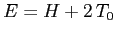 . Poiché
. Poiché 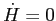
ESERCIZIO B.5 a,b) L'equazione caratteristica della matrice 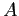 del sistema dinamico è
del sistema dinamico è
e quindi c'è il solo autovalore 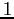 , la matrice non è diagonalizzabile. Gli autovettori sono soltanto i vettori con componenti uguali, per esempio il versore
, la matrice non è diagonalizzabile. Gli autovettori sono soltanto i vettori con componenti uguali, per esempio il versore
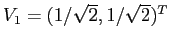 . Per mettere la parte nilpotente in forma semplice basta prendere un vettore che non sia multiplo di
. Per mettere la parte nilpotente in forma semplice basta prendere un vettore che non sia multiplo di 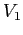 ,
, 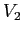 , e calcolare l'effetto su di esso della parte nilpotente di
, e calcolare l'effetto su di esso della parte nilpotente di 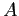 :
:
Il valore 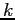 dipende dalla scelta fatta per
dipende dalla scelta fatta per 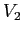 , per esempio se si sceglie
, per esempio se si sceglie
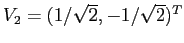 si trova
si trova  e quindi il cambiamento di coordinate definito dalla nuova base
e quindi il cambiamento di coordinate definito dalla nuova base 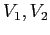
la cui esponenziale di matrice è semplice:
da cui si calcola l'esponenziale della matrice 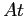 :
:
da cui segue l'espressione della soluzione con condizioni iniziali 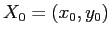 :
:
che tendono tutte a 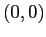 per
per 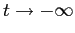 .
.
ESERCIZIO B.6 a) L'equazione alle differenze finite del secondo ordine è:
che si trasforma nel sistema dinamico discreto:
b) I punti fissi sono definiti dalle equazioni
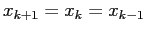 , da cui
, da cui 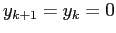 per definizione di
per definizione di 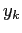 . Allora
. Allora
da cui i punti fissi
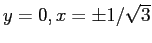 coincidono con i punti di equilibrio del sistema dinamico continuo di partenza.
coincidono con i punti di equilibrio del sistema dinamico continuo di partenza.
c) La matrice jacobiana
ha determinante 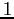 e traccia
e traccia 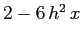 , quindi il discriminante dell'equazione caratteristica è
, quindi il discriminante dell'equazione caratteristica è
In 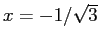
e ci sono due radici reali distinte, positive, una maggiore ed una minore di 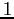 , quindi un punto fisso iperbolico.
, quindi un punto fisso iperbolico.
d) Per 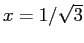 il discriminante è
il discriminante è
che è negativo per
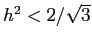 ; poichè il determinante è
; poichè il determinante è 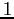 , per tali valori di
, per tali valori di 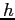 si hanno due autovalori complessi coniugati di modulo
si hanno due autovalori complessi coniugati di modulo 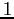 e il punto fisso è ellittico.
e il punto fisso è ellittico.
ESERCIZIO B.7 a) Le coordinate degli estremi dell'asta sono:
e quindi quelle del punto materiale:
b) L'energia cinetica e potenziale sono
c) La lagrangiana
e il momento, cioè l'inversa della trasformazione di Legendre:
da cui la hamiltoniana
e le equazioni di Hamilton:
d) I punti di equilibrio si ottengono ponendo  , e quindi
, e quindi 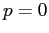 , e poi imponendo
, e poi imponendo 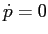 ma con la seconda equazione di Hamilton semplificata tenendo conto di
ma con la seconda equazione di Hamilton semplificata tenendo conto di 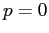 :
:
da cui i punti di equilibrio sono per 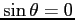 cioè
cioè
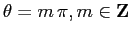 . Calcoliamo le derivate seconde di
. Calcoliamo le derivate seconde di 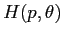 tenendo conto di
tenendo conto di 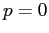 ; ne segue che le derivate seconde miste sono nulle, mentre la derivata seconda rispetto a
; ne segue che le derivate seconde miste sono nulle, mentre la derivata seconda rispetto a 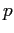 è sempre positiva (condizione di convessità). Resta da vedere il segno di
è sempre positiva (condizione di convessità). Resta da vedere il segno di
che è maggiore di zero in
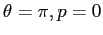 che quindi è un minimo di
che quindi è un minimo di 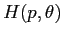 , e perciò è stabile, non asintoticamente stabile (usando
, e perciò è stabile, non asintoticamente stabile (usando 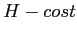 come funzione di Lyapounov). Invece in
come funzione di Lyapounov). Invece in 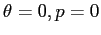 ha un determinante hessiano negativo, e quindi è una sella. Si può verificare che il linearizzato delle equazioni di Hamilton ha autovalori di segno discorde, e quindi si tratta di una sella nonlineare, instabile perché da essa esce una separatrice instabile.
ha un determinante hessiano negativo, e quindi è una sella. Si può verificare che il linearizzato delle equazioni di Hamilton ha autovalori di segno discorde, e quindi si tratta di una sella nonlineare, instabile perché da essa esce una separatrice instabile.
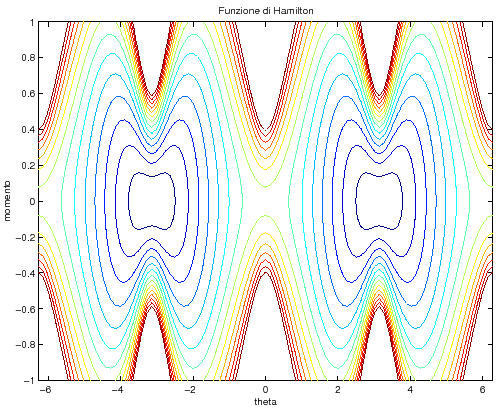
Figura C.13:
Curve di livello della funzione di Hamilton, per 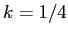 . Si noti che le coordinate sono
. Si noti che le coordinate sono 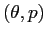 (per rendere più facile il confronto con la figura sotto).
(per rendere più facile il confronto con la figura sotto).
 |
e) Per 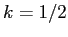 il coefficiente di
il coefficiente di 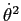 in
in 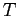 è una costante, e quindi le curve di livello sono le stesse di un pendolo ordinario. Per valori di
è una costante, e quindi le curve di livello sono le stesse di un pendolo ordinario. Per valori di 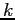 significativamente diversi da
significativamente diversi da 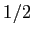 le curve di livello sono molto diverse nel caso della funzione di Hamilton nel piano
le curve di livello sono molto diverse nel caso della funzione di Hamilton nel piano 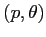 (Figura C.13) e della funzione energia nel piano
(Figura C.13) e della funzione energia nel piano
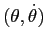 (Figura C.14).
(Figura C.14).
Figura C.14:
Curve di livello della funzione energia, per 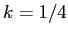 .
.
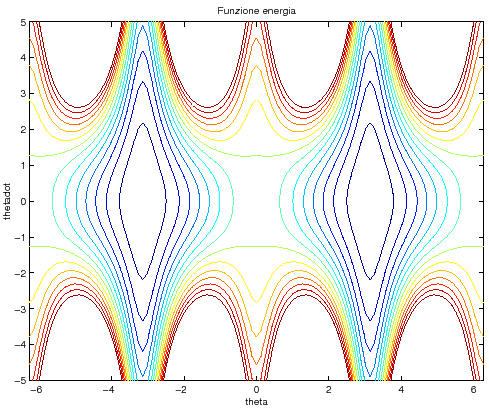 |
f) Il valore della hamiltoniana in
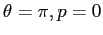 è
è
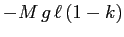 , mentre il valore alla sella
, mentre il valore alla sella 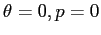 è
è
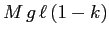 . Perciò la differenza di energia tra il punto di equilibrio stabile e le separatrici è
. Perciò la differenza di energia tra il punto di equilibrio stabile e le separatrici è
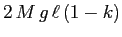 . Per avere un'orbita che stia al di fuori (o sopra, o sotto) delle separatrici delle selle occorre un'energia cinetica
. Per avere un'orbita che stia al di fuori (o sopra, o sotto) delle separatrici delle selle occorre un'energia cinetica
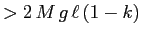 , da cui
, da cui
Andrea Milani
2009-06-01
![]() . La matrice della nuova base
. La matrice della nuova base
![\begin{displaymath}B^{-1}=\left[\begin{array}{ccc}
{8}&{\phantom{-}0}&{0}\\ {2}&{-2}&{0}\\ {1}&{\phantom{-}0}&{1}\end{array}\right] \ , \end{displaymath}](img2992.png)
![\begin{displaymath}B= \frac 18 \;\left[\begin{array}{ccc}
{\phantom{-}1}&{\phant...
...ntom{-}1}&{-4}&{0}\\ {-1}&{\phantom{-}0}&{8}\end{array}\right] \end{displaymath}](img2994.png)
![\begin{displaymath}B^{-1} \; \left[\begin{array}{ccc}
{e^t}&{0}&{0}\\ {0}&{e^{-t...
...}\\ {0}&{e^{-t}\sin 2t}&{e^{-t}\cos 2t}\end{array}\right] \; B \end{displaymath}](img2995.png)
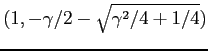 , cioè verso l'alto a sinistra, e poi piega verso il basso, quindi passa a sinistra del punto
, cioè verso l'alto a sinistra, e poi piega verso il basso, quindi passa a sinistra del punto ![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle x_{k+1}} & {\displ...
...t[2x_k-4x_k^3\right]+ (1-h\gamma)\,y_k}
\end{array}\right.\ . \end{displaymath}](img3014.png)
![\begin{displaymath}DS(x,y)=\left[\begin{array}{cc}{1 + h^2\,(2-12x^2)}&{h(1-h\gamma)}\\
{h\,(2-12x^2)}&{1-h\gamma}\end{array}\right] \end{displaymath}](img3018.png)
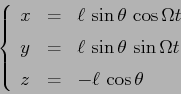
![\begin{displaymath}H(p,\theta)=\frac{p^2}{2\,m\,\ell^2} - m\,\ell^2\; \left[ \frac{\Omega^2}{2}\, \sin^2\theta + \frac g\ell\;\cos\theta \right] \end{displaymath}](img3037.png)
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle \dot \theta} & {\d...
...t[\Omega^2\,\cos\theta-\frac g\ell\right]}
\end{array}\right. \end{displaymath}](img3038.png)
![\begin{displaymath}\frac{\partial {(\dot\theta, \dot p)}}{\partial {(\theta, p)}...
...ga^2\,\cos 2\theta-\cos\theta\; g/\ell)}&{0}\end{array}\right] \end{displaymath}](img3043.png)
![]() del sistema dinamico è
del sistema dinamico è
![\begin{displaymath}V=\left[V_1 \; V_2\right]=\frac 1{\sqrt{2}} \left[\begin{arra...
...\left[\begin{array}{cc}{1}&{2}\\
{0}&{1}\end{array}\right]=C \end{displaymath}](img3064.png)
![\begin{displaymath}\exp(Ct) = e^t\; \left[\begin{array}{cc}{1}&{2t}\\
{0}&{1}\end{array}\right] \ . \end{displaymath}](img3065.png)
![\begin{displaymath}\exp(At)= V\, \exp(Ct)\, V^{-1}= e^t\, \left[\begin{array}{cc}{1+t}&{-t}\\
{+t}&{1-t}\end{array}\right] \end{displaymath}](img3067.png)
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle x(t)} & {\displays...
...&{\displaystyle e^t\,[t\,x_0 +(1-t)\,y_0]}
\end{array}\right. \end{displaymath}](img3069.png)
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle x_{k+1}} & {\displ...
...k+1}-x_k}h=y_k + h\,\left[1-3x_k^2\right]}
\end{array}\right. \end{displaymath}](img3071.png)
![\begin{displaymath}DS(x,y)=\left[\begin{array}{cc}{1-6\,h^2\, x}&{h}\\
{-6\,h\,x}&{1}\end{array}\right] =A(x) \end{displaymath}](img3076.png)
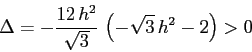
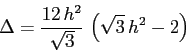
![\begin{displaymath}H(p,\theta)= \frac{p^2}{2\,M\,\ell^2 \,\left[ k^2\,\cos^2\the...
...1-k)^2\, \sin^2\theta\right]} + M\,g\,\ell\,(1-k)\, \cos\theta \end{displaymath}](img3090.png)
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle \dot\theta} & {\di...
...\theta + (1-k)^2\, \sin^2\theta\right]^2}}
\end{array}\right. \end{displaymath}](img3091.png)