Next: C.2 Soluzioni del capitolo Up: C. SOLUZIONI DI TUTTI Previous: C. SOLUZIONI DI TUTTI Indice Indice analitico
![]() .
.
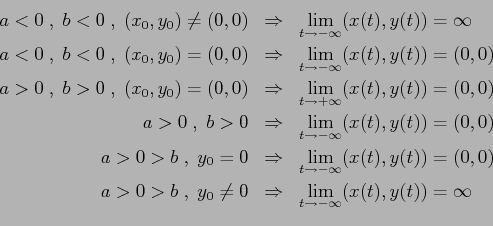
![]() . Se esiste una soluzione
. Se esiste una soluzione ![]() su di un intervallo
su di un intervallo
![]() , in ogni sottointervallo
, in ogni sottointervallo
![]() di monotonia di
di monotonia di ![]() esiste l'inversa
esiste l'inversa ![]() ; poiché
; poiché ![]() è sempre
è sempre ![]() ,
, ![]() e vale
e vale
![]() e
e
![]() , funzione bigettiva da
, funzione bigettiva da ![]() in
in ![]() . Dunque il sistema ammette soluzioni definite su tutto
. Dunque il sistema ammette soluzioni definite su tutto ![]() , per ogni condizione iniziale
, per ogni condizione iniziale ![]() .
.