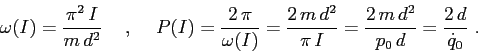ESERCIZIO 5.1 La costante 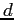 non conta. Se
non conta. Se  si ottiene un sistema dinamico lineare, il cui punto di equilibrio sarà una sella o un centro a seconda dei casi. Avendo ridotto il potenziale, a meno di una costante, a
si ottiene un sistema dinamico lineare, il cui punto di equilibrio sarà una sella o un centro a seconda dei casi. Avendo ridotto il potenziale, a meno di una costante, a
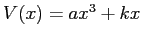 (in effetti
(in effetti 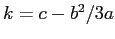 ) si può supporre
) si può supporre 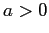 (a meno di scambiare
(a meno di scambiare 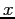 con
con 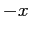 ); perciò l'andamento qualitativo delle curve di livello dipende solo dal segno di
); perciò l'andamento qualitativo delle curve di livello dipende solo dal segno di 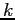 . Per
. Per 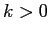 l'energia potenziale non ha né massimi né minimi, e tutte le orbite sono curve aperte, con
l'energia potenziale non ha né massimi né minimi, e tutte le orbite sono curve aperte, con
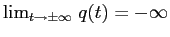 . Per
. Per  si ha un punto di equlibrio instabile con linearizzato degenere (come in Figura 3.2), per
si ha un punto di equlibrio instabile con linearizzato degenere (come in Figura 3.2), per 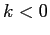 si hanno un massimo ed un minimo, corrispondenti ad un punto di equlibrio stabile e ad una sella. Le separatrici della sella si congiungono dal lato delle
si hanno un massimo ed un minimo, corrispondenti ad un punto di equlibrio stabile e ad una sella. Le separatrici della sella si congiungono dal lato delle 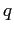 positive, girando attorno al punto stabile.
positive, girando attorno al punto stabile.
ESERCIZIO 5.2 Studiare solo per 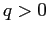 ; il resto si ottiene per simmetria, cioè con la sostituzione
; il resto si ottiene per simmetria, cioè con la sostituzione 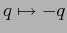 .
.
dove possiamo scegliere  . Studiamo sistematicamente i limiti dell'energia potenziale per
. Studiamo sistematicamente i limiti dell'energia potenziale per  che tende agli estremi dell'insieme di definizione: se
che tende agli estremi dell'insieme di definizione: se
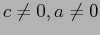
Inoltre troviamo quanti zeri ha la funzione 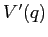 per
per 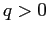 , il che dipenderà anche dal segno di
, il che dipenderà anche dal segno di 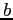 e dal segno di
e dal segno di
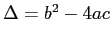 .
.
ESERCIZIO 5.3 Cè un solo punto di equilibrio nell'origine. Infatti
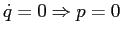 e
e
quindi il punto di equilibrio è l'origine, il linearizzato ha matrice
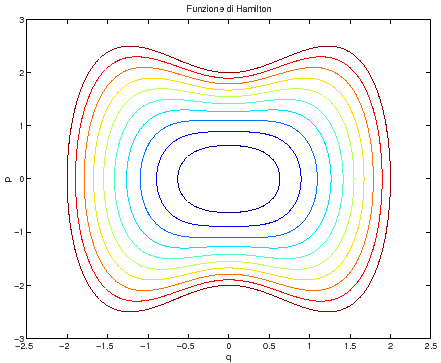
ed è comunque stabile, visto che 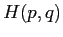 ha un minimo. Le curve di livello sono tracciate nella Figura C.5.
ha un minimo. Le curve di livello sono tracciate nella Figura C.5.
A titolo di esempio, il programma utilizzato per generare questa figura è ham_lev53.m ..
Figura C.5:
Curve di livello della funzione di Hamilton.
 |
ESERCIZIO 5.4
ESERCIZIO 5.5
ESERCIZIO 5.6 Dalla forma dell'energia cinetica si deduce che
ESERCIZIO 5.7 La coordinata 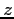 ha senso solo per
ha senso solo per 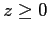 . La funzione di Hamilton è
. La funzione di Hamilton è
Poiché
le curve di livello sono limitate per 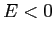 , illimitate per
, illimitate per 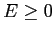 . Nel primo caso l'orbita ricade sulla superficie
. Nel primo caso l'orbita ricade sulla superficie  dopo un tempo finito, nel secondo va all'infinito. La funzione energia è
dopo un tempo finito, nel secondo va all'infinito. La funzione energia è
quindi la velocità iniziale critica che separa i due casi è
Il tempo per arrivare all'altezza 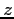 , partendo da
, partendo da  al tempo
al tempo 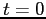 , è espresso dalla quadratura
, è espresso dalla quadratura
ESERCIZIO 5.8
L'equazione di Lagrange è
con secondo membro costante, quindi le soluzioni sono funzioni quadratiche del tempo.
ESERCIZIO 5.9 Rispetto alle coordinate indicate in figura, risulta
da cui derivando e sfruttando alcune cancellazioni
le energie cinetica e potenziale sono date da
e dalla lagrangiana
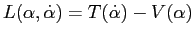 si ottiene, per
si ottiene, per
la hamiltoniana 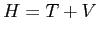
Si noti che le equazioni di moto diventano non risolvibili rispetto alla derivata seconda quando
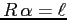 , cioè quando il pendolo sbatte sul cilindro. Intorno al punto di equilibrio stabile
, cioè quando il pendolo sbatte sul cilindro. Intorno al punto di equilibrio stabile 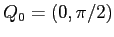 ,
, 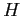 ha la forma
ha la forma
approssimando le piccole oscillazioni intorno a 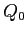 con quelle del sistema (lineare) con hamiltoniana
con quelle del sistema (lineare) con hamiltoniana 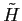 , si ottengono ellissi (le curve di livello
, si ottengono ellissi (le curve di livello  ) del tipo
) del tipo
Nell'approssimazione scompare la dipendenza del periodo dall'energia:
ESERCIZIO 5.10 Si ottengono l'energia cinetica e l'energia potenziale
da cui la lagrangiana 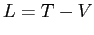 e l'hamiltoniana
e l'hamiltoniana
i cui punti di equilibrio sono solo per 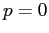 e tali che
e tali che
per cui ci sono due punti di equilibrio
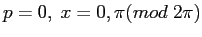 con linearizzato
con linearizzato
che ha traccia nulla. Il determinante è 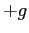 per
per 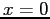 , quindi
, quindi 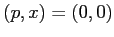 è stabile, e
è stabile, e 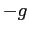 per
per  , quindi
, quindi 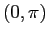 è una sella. Si noti che i punti di equilibrio hanno la stessa stabilità, quindi il sistema ha lo stesso comportamento qualitativo del pendolo ordinario
è una sella. Si noti che i punti di equilibrio hanno la stessa stabilità, quindi il sistema ha lo stesso comportamento qualitativo del pendolo ordinario
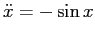 , ma il sistema non è lo stesso, come si vede dalla Figura C.6.
, ma il sistema non è lo stesso, come si vede dalla Figura C.6.
Figura C.6:
Curve di livello della funzione di Hamilton.
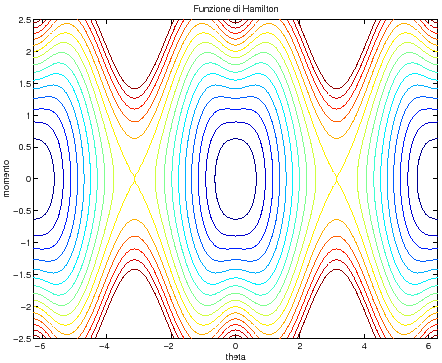 |
ESERCIZIO 5.11 In un piano verticale 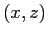 perpendicolare all'asse del cilindro, le coordinate dell'intersezione con l'asse del cilindro sono
perpendicolare all'asse del cilindro, le coordinate dell'intersezione con l'asse del cilindro sono
Figura C.7:
Cilindro che rotola su di un piano inclinato.
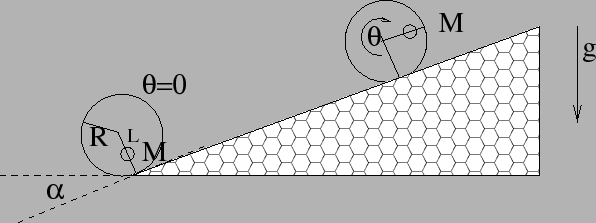 |
assumendo un sistema di riferimento tale che a  corrisponda
corrisponda 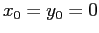 . (Si noti che il cilindro ruota in verso orario, quindi con
. (Si noti che il cilindro ruota in verso orario, quindi con 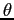 decrescente, se sale il piano inclinato.) Da questo segue la parametrizzazione suggerita, aggiungendo vettorialmente la rotazione attorno all'asse del cilindro. La velocità del punto materiale è
decrescente, se sale il piano inclinato.) Da questo segue la parametrizzazione suggerita, aggiungendo vettorialmente la rotazione attorno all'asse del cilindro. La velocità del punto materiale è
e l'energia cinetica
L'energia potenziale è proporzionale all'altezza:
La lagrangiana
definisce il momento
e l'equazione di Lagrange
La hamiltoniana
definisce equazioni di Hamilton con punti di equilibrio solo dove
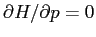 , che avviene solo per
, che avviene solo per 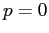 perchè
perchè 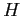 è quadratica in
è quadratica in 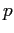 , e dove
, e dove
che ha soluzione solo se
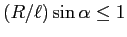 ; si noti che il parametro
; si noti che il parametro 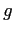 non ha influenza sulla presenza di equilibri. Se la condizione
non ha influenza sulla presenza di equilibri. Se la condizione
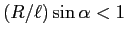 è soddisfatta, per ogni giro
è soddisfatta, per ogni giro
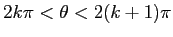 ci sono due equilibri, con la stabilità controllata dal segno di
ci sono due equilibri, con la stabilità controllata dal segno di
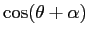 , quindi un equilibrio stabile e una sella.
, quindi un equilibrio stabile e una sella.
ESERCIZIO 5.12 La parametrizzazione del moto
porta, grazie alla semplificazione
![$[r'(q)]^2+[z'(q)]^2=R^2$](img2921.png) all'energia cinetica e potenziale
all'energia cinetica e potenziale
da cui 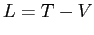 . Il momento è
. Il momento è
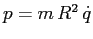 e l'equazione di Lagrange
e l'equazione di Lagrange
La hamiltoniana
definisce le equazioni di Hamilton
e non coincide con l'energia, che vale
ESERCIZIO 5.13 Se 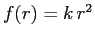 , allora
, allora 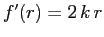 e dalle formule date nel testo
e dalle formule date nel testo
con equilibri solo per 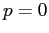 .
.
da cui 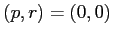 è il solo punto di equilibrio; il linearizzato
è il solo punto di equilibrio; il linearizzato
ha determinante
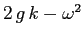 . Perciò per
. Perciò per
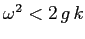 si ha un punto stabile, per
si ha un punto stabile, per
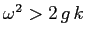 una sella.
una sella.
ESERCIZIO 5.14
con equilibri solo per 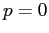 e
e
per cui ci sono degli equilibri in corrispondenza delle soluzioni di
Figura C.8:
Le intersezioni della sinusoide con le rette inclinate sono tanto più numerose quanto più bassa è l'inclinazione.
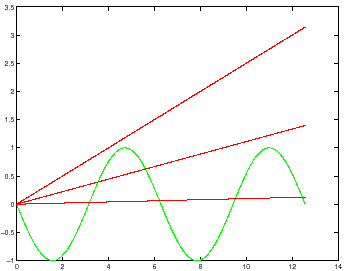 |
che esistono per 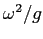 non troppo grande, e sono tanto più numerose quanto più piccolo è
non troppo grande, e sono tanto più numerose quanto più piccolo è 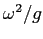 (si vedano i diversi casi, a seconda del valore di
(si vedano i diversi casi, a seconda del valore di 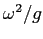 , nella Figura C.8). Gli equilibri sono generalmente a coppie, in ogni coppia quello con
, nella Figura C.8). Gli equilibri sono generalmente a coppie, in ogni coppia quello con 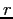 più piccolo corrisponde ad un minimo di
più piccolo corrisponde ad un minimo di 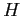 e quindi è stabile, l'altro è una sella.
e quindi è stabile, l'altro è una sella.
ESERCIZIO 5.15 Qualunque sia la funzione 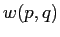 da usare in combinazione con
da usare in combinazione con 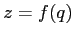 , la matrice jacobiana sarà della forma:
, la matrice jacobiana sarà della forma:
che ha determinante 1 se e solo se
dove 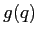 è una funzione
è una funzione 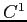 arbitraria.
arbitraria.
PROBLEMA 5.16 Il discriminante dell'equazione caratteristica è
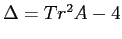 , per cui
, per cui 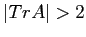 porta a radici reali
porta a radici reali
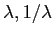 con
con 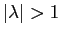 . Tutte le matrici con questi autovalori possono essere descritte come
. Tutte le matrici con questi autovalori possono essere descritte come
dove 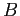 è una qualunque matrice invertibile
è una qualunque matrice invertibile 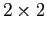 . Invece
. Invece 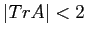 porta a radici complesse
porta a radici complesse
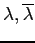 con
con 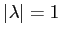 . Tutte le matrici con questi autovalori sono della forma
. Tutte le matrici con questi autovalori sono della forma
dove 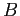 è una qualunque matrice invertibile e
è una qualunque matrice invertibile e 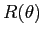 è la rotazione di un angolo
è la rotazione di un angolo
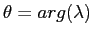 . Resta il caso
. Resta il caso 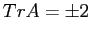 in cui l'autovalore
in cui l'autovalore 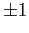 è doppio, quindi o
è doppio, quindi o 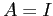 oppure
oppure 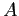 è coniugata alla forma canonica
è coniugata alla forma canonica 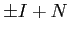 con
con 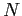 una matrice nilpotente (si veda l'esercizio 2.10).
una matrice nilpotente (si veda l'esercizio 2.10).
ESERCIZIO 5.17 La matrice jacobiana è
con determinante identicamente 1, La funzione generatrice soddisfa alle equazioni alle derivate parziali:
che sono soddisfatte da
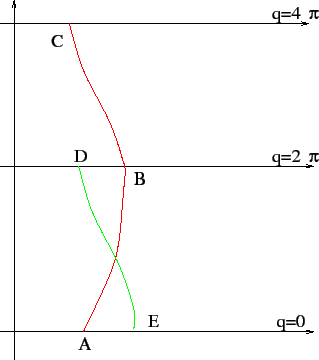
PROBLEMA 5.18 Si faccia riferimento alla Figura C.9: supponiamo per esempio che l'orbita periodica si richiuda dopo un incremento di 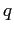 di
di 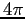 , come la curva
, come la curva 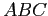 , dove il valore di
, dove il valore di 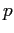 in
in 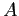 ed in
ed in 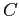 deve essere uguale, chiamiamolo
deve essere uguale, chiamiamolo 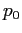 . Il valore di
. Il valore di 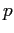 in
in 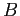 sia, per ipotesi, diverso da
sia, per ipotesi, diverso da 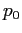 , chiamiamolo
, chiamiamolo 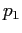 .
.
Figura C.9:
Per richiudersi dopo due giri, l'orbita periodica dovrebbe incrociare se stessa.
 |
Se ora noi consideriamo la curva ottenuta da 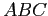 per traslazione di
per traslazione di 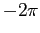 lungo l'asse
lungo l'asse 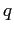 , essa conterrà il tratto
, essa conterrà il tratto 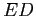 , in cui
, in cui 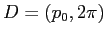 ,
, 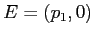 . Ma allora i due archi di curva
. Ma allora i due archi di curva 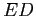 e
e 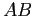 devono incrociarsi, il che contraddice l'unicità delle soluzioni con condizioni iniziali date. Questo riduce ad assurdo l'ipotesi
devono incrociarsi, il che contraddice l'unicità delle soluzioni con condizioni iniziali date. Questo riduce ad assurdo l'ipotesi 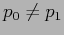 . Se l'incremento di
. Se l'incremento di 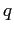 fosse
fosse
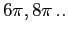 si considererebbero le copie dei vari tratti di orbita riportate all'intervallo
si considererebbero le copie dei vari tratti di orbita riportate all'intervallo ![$[0,2\pi]$](img2040.png) .
.
ESERCIZIO 5.19
PROBLEMA 5.20 Se ci fossero più di due intersezioni con 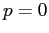 , ce ne sarebbe almeno una, chiamiamola
, ce ne sarebbe almeno una, chiamiamola 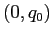 , tale che ad essa tendono segmenti della traiettoria con
, tale che ad essa tendono segmenti della traiettoria con 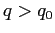 e con
e con 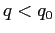 . Data la simmetria rispetto a
. Data la simmetria rispetto a 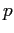 , ci dovrebbero essere quattro di tali rami. Ma allora la traiettoria non sarebbe, in
, ci dovrebbero essere quattro di tali rami. Ma allora la traiettoria non sarebbe, in 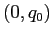 , una curva regolare, ossia non vale il teorema della funzione implicita, quindi
, una curva regolare, ossia non vale il teorema della funzione implicita, quindi 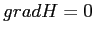 , da cui si tratta di un punto di equilibrio, che non può appartenere ad un'orbita periodica.
, da cui si tratta di un punto di equilibrio, che non può appartenere ad un'orbita periodica.
ESERCIZIO 5.21 Poichè
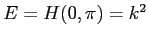 il valore del momento lungo la curva di livello cercata è
il valore del momento lungo la curva di livello cercata è
da cui l'area si calcola con l'integrale
Si può limitarsi a calcolare l'integrale sull'intervallo ![$[0,\pi]$](img2978.png) grazie al fatto che la funzione integranda è pari, e su tale intervallo si può usare la sostituzione
grazie al fatto che la funzione integranda è pari, e su tale intervallo si può usare la sostituzione 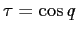 , con la regola di integrazione per sostituzione
, con la regola di integrazione per sostituzione
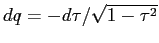 , da cui
, da cui
Quindi il valore di 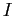 tende a
tende a
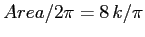 al tendere verso la separatrice della sella.
al tendere verso la separatrice della sella.
PROBLEMA 5.22 Quindi le aree racchiuse dalle orbite periodiche con velocità iniziale 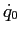 sono dei rettangoli
sono dei rettangoli
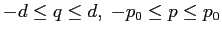 , dove
, dove
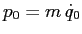 . La loro area è
. La loro area è 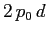 , per cui
, per cui
D'altro canto l'energia è funzione solo del momento
e quindi la relazione tra variabile azione ed energia è
da cui le frequenze proprie ed i periodi
Andrea Milani
2009-06-01
![]() non conta. Se
non conta. Se ![]() si ottiene un sistema dinamico lineare, il cui punto di equilibrio sarà una sella o un centro a seconda dei casi. Avendo ridotto il potenziale, a meno di una costante, a
si ottiene un sistema dinamico lineare, il cui punto di equilibrio sarà una sella o un centro a seconda dei casi. Avendo ridotto il potenziale, a meno di una costante, a
![]() (in effetti
(in effetti ![]() ) si può supporre
) si può supporre ![]() (a meno di scambiare
(a meno di scambiare ![]() con
con ![]() ); perciò l'andamento qualitativo delle curve di livello dipende solo dal segno di
); perciò l'andamento qualitativo delle curve di livello dipende solo dal segno di ![]() . Per
. Per ![]() l'energia potenziale non ha né massimi né minimi, e tutte le orbite sono curve aperte, con
l'energia potenziale non ha né massimi né minimi, e tutte le orbite sono curve aperte, con
![]() . Per
. Per ![]() si ha un punto di equlibrio instabile con linearizzato degenere (come in Figura 3.2), per
si ha un punto di equlibrio instabile con linearizzato degenere (come in Figura 3.2), per ![]() si hanno un massimo ed un minimo, corrispondenti ad un punto di equlibrio stabile e ad una sella. Le separatrici della sella si congiungono dal lato delle
si hanno un massimo ed un minimo, corrispondenti ad un punto di equlibrio stabile e ad una sella. Le separatrici della sella si congiungono dal lato delle ![]() positive, girando attorno al punto stabile.
positive, girando attorno al punto stabile.
![]() ; il resto si ottiene per simmetria, cioè con la sostituzione
; il resto si ottiene per simmetria, cioè con la sostituzione ![]() .
.
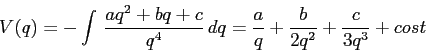
![]() e
e
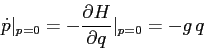
![\begin{displaymath}A=\left[\begin{array}{cc}{0}&{-g}\\
{1}&{0}\end{array}\right] \end{displaymath}](img2862.png)
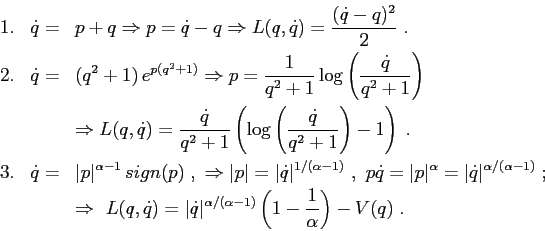
![\begin{eqnarray*}1.&p=&\frac{\dot q}{\sqrt{1-{\dot q}^2}}\Rightarrow {\dot q}^2=...
...q)},\ \Rightarrow H(p,q)=\frac 12\frac{[p-B(q)]^2}{A(q)}+V(q)\;. \end{eqnarray*}](img2865.png)
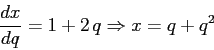
![]() ha senso solo per
ha senso solo per ![]() . La funzione di Hamilton è
. La funzione di Hamilton è
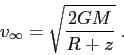
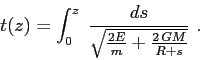
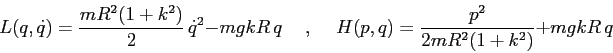
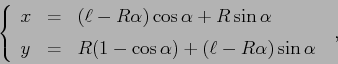
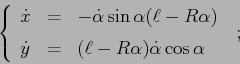
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle T} & {\displaystyl...
...(1-\cos\alpha)+ (\ell-R\alpha)\sin\alpha]}
\end{array}\right. \end{displaymath}](img2878.png)
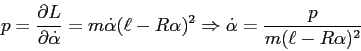
![\begin{displaymath}H(p,\alpha)=\frac{p^2}{2m(\ell-R\alpha)^2}-mg[R(1-\cos\alpha)+ (\ell-R\alpha)\sin\alpha]\;. \end{displaymath}](img2882.png)
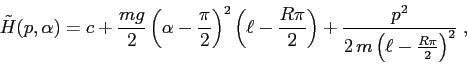
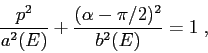
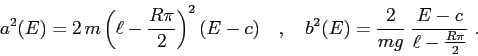
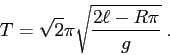
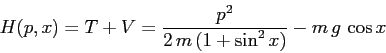
![\begin{displaymath}A(x)= \left[\begin{array}{cc}{0}&{-mg\cos x}\\
{1/m(1+\sin^2 x)}&{0}\end{array}\right] \end{displaymath}](img2898.png)
![]() perpendicolare all'asse del cilindro, le coordinate dell'intersezione con l'asse del cilindro sono
perpendicolare all'asse del cilindro, le coordinate dell'intersezione con l'asse del cilindro sono
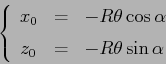
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle \dot x} & {\displa...
...\,\sin\alpha + \ell\,\sin(\theta+\alpha)]}
\end{array}\right. \end{displaymath}](img2908.png)
![\begin{displaymath}H(p,\theta)=\frac{p^2}{2\,M\,\left[R^2+\ell^2 - 2\,R\,\ell\,\...
...,\left[R\, \theta \sin\alpha +\ell\,\cos(\theta+\alpha)\right] \end{displaymath}](img2914.png)
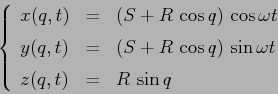
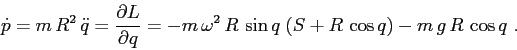
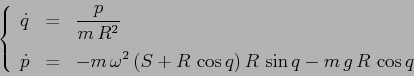
![]() , allora
, allora ![]() e dalle formule date nel testo
e dalle formule date nel testo
![\begin{displaymath}H(p,r)=\frac{p^2}{2\,m\,[1+4\,k^2\,r^2]} -\frac m2\,\omega^2\,r^2 +m\,g\,k\,r^2 \end{displaymath}](img2930.png)
![\begin{displaymath}\frac{\partial {(\dot p, \dot r)}}{\partial {(p,r)}}(0,0)= \l...
...rray}{cc}{0}&{m(\omega^2-2gk)}\\
{1/m}&{0}\end{array}\right] \end{displaymath}](img2933.png)
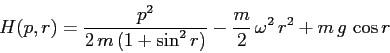
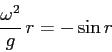

![]() da usare in combinazione con
da usare in combinazione con ![]() , la matrice jacobiana sarà della forma:
, la matrice jacobiana sarà della forma:
![\begin{displaymath}\frac{\partial {(w,z)}}{\partial {(p,q)}}=\left[\begin{array}...
...l p}&{\partial w/\partial q}\\
{0}&{f'(q)}\end{array}\right] \end{displaymath}](img2942.png)
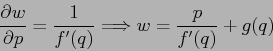
![]() , per cui
, per cui ![]() porta a radici reali
porta a radici reali
![]() con
con ![]() . Tutte le matrici con questi autovalori possono essere descritte come
. Tutte le matrici con questi autovalori possono essere descritte come
![\begin{displaymath}B\, \left[\begin{array}{cc}{\lambda}&{0}\\
{0}&{1/\lambda}\end{array}\right]\, B^{-1} \end{displaymath}](img2948.png)
![\begin{displaymath}\frac{\partial {(w,z)}}{\partial {(p,q)}}=\left[\begin{array}{cc}{1/q}&{-p/q^2}\\
{0}&{q}\end{array}\right] \end{displaymath}](img2957.png)
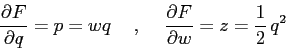
![]() di
di ![]() , come la curva
, come la curva ![]() , dove il valore di
, dove il valore di ![]() in
in ![]() ed in
ed in ![]() deve essere uguale, chiamiamolo
deve essere uguale, chiamiamolo ![]() . Il valore di
. Il valore di ![]() in
in ![]() sia, per ipotesi, diverso da
sia, per ipotesi, diverso da ![]() , chiamiamolo
, chiamiamolo ![]() .
.
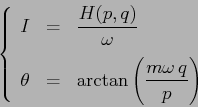
![]() , ce ne sarebbe almeno una, chiamiamola
, ce ne sarebbe almeno una, chiamiamola ![]() , tale che ad essa tendono segmenti della traiettoria con
, tale che ad essa tendono segmenti della traiettoria con ![]() e con
e con ![]() . Data la simmetria rispetto a
. Data la simmetria rispetto a ![]() , ci dovrebbero essere quattro di tali rami. Ma allora la traiettoria non sarebbe, in
, ci dovrebbero essere quattro di tali rami. Ma allora la traiettoria non sarebbe, in ![]() , una curva regolare, ossia non vale il teorema della funzione implicita, quindi
, una curva regolare, ossia non vale il teorema della funzione implicita, quindi ![]() , da cui si tratta di un punto di equilibrio, che non può appartenere ad un'orbita periodica.
, da cui si tratta di un punto di equilibrio, che non può appartenere ad un'orbita periodica.
![]() il valore del momento lungo la curva di livello cercata è
il valore del momento lungo la curva di livello cercata è
![\begin{eqnarray*}Area&=& k\,4\,\sqrt{2} \int_{-1}^{+1}\; \frac{\sqrt{1-\tau}}{\s...
...}}= k\,8\,\sqrt{2} \left[ \sqrt{1+\tau}\right]_{-1}^{+1}= 16\, k \end{eqnarray*}](img2981.png)
![]() sono dei rettangoli
sono dei rettangoli
![]() , dove
, dove
![]() . La loro area è
. La loro area è ![]() , per cui
, per cui