ESERCIZIO 4.1 In termini della matrice compagna  dell'equazione, il problemi hanno soluzione
dell'equazione, il problemi hanno soluzione
- Calcolando la forma canonica di
 , risulta
, risulta
quindi la successione di Fibonacci è calcolabile con
- Gli autovalori
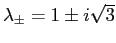 di
di
sono complessi, e la forma canonica di  è la rappresentazione matriciale di
è la rappresentazione matriciale di 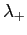 rispetto alla base costituita da parte reale e parte immaginaria di un autovettore di
rispetto alla base costituita da parte reale e parte immaginaria di un autovettore di 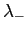 :
:
Allora
e le orbite non sono in genere limitate.
- La molteplicità algebrica dell'unico autovalore
 di
di  è 2, mentre l'autospazio ha dimensione 1, generato da
è 2, mentre l'autospazio ha dimensione 1, generato da 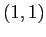 . La forma canonica è
. La forma canonica è
Per
![$N=\left[\begin{array}{cc}{0}&{1}\\
{0}&{0}\end{array}\right]$](img2814.png) si calcola
si calcola
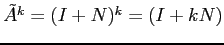 , ovvero
, ovvero
Le orbite sono "rettilinee" se 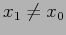 : i punti della bisettrice sono punti fissi della mappa.
: i punti della bisettrice sono punti fissi della mappa.
ESERCIZIO 4.2 La matrice  del sistema dinamico continuo e la matrice
del sistema dinamico continuo e la matrice 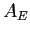 del sistema dinamico discretizzato con il metodo di Eulero sono
del sistema dinamico discretizzato con il metodo di Eulero sono
con autovalori 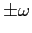 e
e
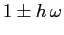 , rispettivamente. Gli autospazi coincidono, cioè
, rispettivamente. Gli autospazi coincidono, cioè 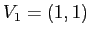 è autovettore di autovalore
è autovettore di autovalore 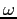 per
per  e di autovalore
e di autovalore 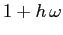 per
per 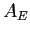 ;
; 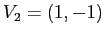 è autovettore di autovalore
è autovettore di autovalore 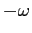 per
per  e di autovalore
e di autovalore 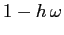 per
per 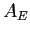 . Quindi le condizioni iniziali parallele a
. Quindi le condizioni iniziali parallele a 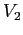 hanno limite
hanno limite 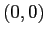 per
per 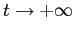 , tutte le altre tendono all'infinito, sia nel sistema continuo che in quello discreto.
, tutte le altre tendono all'infinito, sia nel sistema continuo che in quello discreto.
ESERCIZIO 4.3 Il sistema dinamico discreto è:
con gli autovalori di  :
:
che sono gli inversi di quelli che si ottengono con le differenze in avanti. Perciò le soluzioni del sistema discretizzato decrescono come
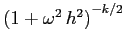 e tendono a 0 per
e tendono a 0 per 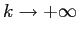 .
.
PROBLEMA 4.4
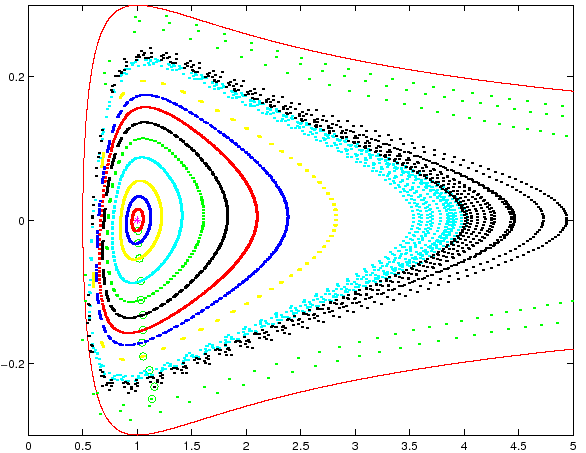
Figura C.4:
Alcune orbite della mappa standard del problema dei due corpi. La curva di livello zero dell'energia ha proprietà analoghe a quelle di una separatrice.
 |
La mappa standard
ha il solo punto fisso
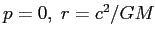 corrispondente al punto di equilibrio stabile (orbita circolare) del sistema continuo. A titolo di esempio, la Figura C.4 mostra il comportamento di alcune orbite per
corrispondente al punto di equilibrio stabile (orbita circolare) del sistema continuo. A titolo di esempio, la Figura C.4 mostra il comportamento di alcune orbite per  . La curva continua è la curva di livello
. La curva continua è la curva di livello 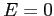 .
.
ESERCIZIO 4.5 L'equazione alle differenze finite del secondo ordine
si riduce ad un sistema dinamico discreto usando, per esempio,
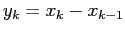 :
:
da cui
che ha come punti fissi 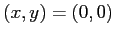 e
e 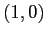 , coincidenti con i punti di equilibrio del sistema discreto. Il punto
, coincidenti con i punti di equilibrio del sistema discreto. Il punto 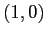 è un pozzo per il sistema continuo, asintoticamente stabile anche per il sistema discreto per
è un pozzo per il sistema continuo, asintoticamente stabile anche per il sistema discreto per 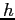 abbastanza piccolo (si calcoli il polinomio caratteristico in
abbastanza piccolo (si calcoli il polinomio caratteristico in 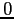 e in
e in 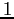 ). Il punto
). Il punto 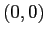 ha per il sistema continuo un linearizzato degenere, e dallo studio delle curve di livello (localmente come nella Figura 3.2) si deduce che è instabile. Nel sistema discreto il linearizzato in
ha per il sistema continuo un linearizzato degenere, e dallo studio delle curve di livello (localmente come nella Figura 3.2) si deduce che è instabile. Nel sistema discreto il linearizzato in 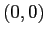 ha matrice
ha matrice
con autovalori
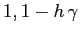 . perciò la mappa linearizzata è stabile, non asintoticamente stabile in questo punto. Dunque per quanto piccolo sia
. perciò la mappa linearizzata è stabile, non asintoticamente stabile in questo punto. Dunque per quanto piccolo sia 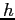 non conosciamo, almeno con gli strumenti studiati in questo corso, le proprietà di stabilità in
non conosciamo, almeno con gli strumenti studiati in questo corso, le proprietà di stabilità in 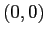 del sistema discreto e non possiamo rispondere alla domanda.
del sistema discreto e non possiamo rispondere alla domanda.
ESERCIZIO 4.6 Se 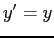 allora
allora 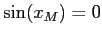 ,
,
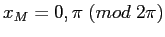 . Da
. Da 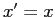 si deduce
si deduce
da cui 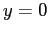 ,
, 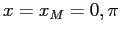 .
.
ESERCIZIO 4.7 I seguenti programmi sono scritti seguendo la sintassi del linguaggio Matlab.
a) Il più semplice programma per eseguire esperimenti sulla mappa standard: stmap1.m . Uso: dare hold off per inizializzare la figura, e assegnare 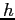 ; per ogni orbita, assegnare le condizioni
; per ogni orbita, assegnare le condizioni 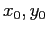 e il numero di iterate
e il numero di iterate 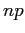 e quindi eseguire stmap1.
e quindi eseguire stmap1.
b) Un semplice programma per il metodo simplettico a tre scorrimenti, sempre applicato alla discretizzazione del pendolo nonlineare: symp2.m . Uso: come sopra.
c) Idem per il metodo di Runge-Kutta implicito ad un passo intermedio: rkimp2.m .
d) Idem per il metodo di Runge-Kutta classico: rk4.m .
Andrea Milani
2009-06-01
![]() dell'equazione, il problemi hanno soluzione
dell'equazione, il problemi hanno soluzione
![\begin{displaymath}\left[\begin{array}{c}{x_k}\\
{x_{k+1}}\end{array}\right]=A^k\,\left[\begin{array}{c}{x_0}\\
{x_1}\end{array}\right]\;. \end{displaymath}](img2798.png)
![\begin{displaymath}A^k={\left[\begin{array}{cc}{0}&{1}\\
{1}&{1}\end{array}\ri...
...\sqrt5)/2]^k}&{0}\\
{0}&{[(1-\sqrt5)/2]^k}\end{array}\right] \end{displaymath}](img2799.png)
![\begin{displaymath}V=\left[\begin{array}{cc}{2}&{2}\\
{1+\sqrt5}&{1-\sqrt5}\en...
...y}{cc}{\sqrt5-1}&{2}\\
{\sqrt5+1}&{-2}\end{array}\right] \;; \end{displaymath}](img2800.png)
![\begin{displaymath}x_{k+1}=\frac{\sqrt5}5\left [\left ( \frac{1+\sqrt5}2\right )^{k+2} -\left (\frac{1-\sqrt5}2\right )^{k+2} \right ]\;. \end{displaymath}](img2801.png)
![\begin{displaymath}A=\left[\begin{array}{cc}{0}&{1}\\
{-4}&{2}\end{array}\right] \end{displaymath}](img2803.png)
![\begin{displaymath}\tilde A=\left[\begin{array}{cc}{1}&{-\sqrt3}\\
{\sqrt3}&{1...
...ay}{cc}{1}&{0}\\
{1/\sqrt3}&{-1/\sqrt3}\end{array}\right]\;, \end{displaymath}](img2807.png)
![\begin{displaymath}\left[\begin{array}{c}{x_k}\\
{x_{k+1}}\end{array}\right]=V...
...\cos[(k-1)\pi/3]}\\
{\sin[(k-1)\pi/3]}\end{array}\right] \;, \end{displaymath}](img2809.png)
![\begin{displaymath}A=\left[\begin{array}{cc}{0}&{1}\\
{-1}&{2}\end{array}\right]=V\,\tilde A\, V^{-1}\;, \end{displaymath}](img2812.png)
![\begin{displaymath}\tilde A=\left[\begin{array}{cc}{1}&{1}\\
{0}&{1}\end{array...
...eft[\begin{array}{cc}{1}&{0}\\
{-1}&{1}\end{array}\right]\;. \end{displaymath}](img2813.png)
![$N=\left[\begin{array}{cc}{0}&{1}\\
{0}&{0}\end{array}\right]$](img2814.png) si calcola
si calcola
![\begin{displaymath}\left[\begin{array}{c}{x_k}\\
{x_{k+1}}\end{array}\right]=V...
...t] +\left[\begin{array}{c}{x_0}\\
{x_1}\end{array}\right]\;. \end{displaymath}](img2816.png)
![]() del sistema dinamico continuo e la matrice
del sistema dinamico continuo e la matrice ![]() del sistema dinamico discretizzato con il metodo di Eulero sono
del sistema dinamico discretizzato con il metodo di Eulero sono
![\begin{displaymath}A=\left[\begin{array}{cc}{0}&{\omega}\\
{\omega}&{0}\end{ar...
...rray}{cc}{1}&{h\,\omega}\\
{h\,\omega}&{1}\end{array}\right] \end{displaymath}](img2819.png)
![\begin{displaymath}\left[\begin{array}{c}{x_{k-1}}\\
{x_k}\end{array}\right]=A...
...{-1/(1+\omega^2\,h^2)}&{2/(1+\omega^2\,h^2)}\end{array}\right] \end{displaymath}](img2827.png)

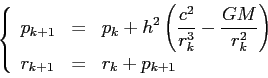
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle x_{k+1}} & {\displ...
...\,\gamma) +h^2\, \left[x_k^2-x_k^3\right]}
\end{array}\right. \end{displaymath}](img2837.png)
![\begin{displaymath}A=\left[\begin{array}{cc}{1}&{1-h\,\gamma}\\
{0}&{1-h\,\gamma}\end{array}\right] \end{displaymath}](img2838.png)
![]() allora
allora ![]() ,
,
![]() . Da
. Da ![]() si deduce
si deduce
![]() ; per ogni orbita, assegnare le condizioni
; per ogni orbita, assegnare le condizioni ![]() e il numero di iterate
e il numero di iterate ![]() e quindi eseguire stmap1.
e quindi eseguire stmap1.