Next: 3.5 GRADIENTI Up: 3. TEORIA QUALITATIVA Previous: 3.3 FUNZIONI DI LYAPOUNOV Indice Indice analitico
Sommario I sistemi newtoniani sono quelli in cui è assegnata
un'accelerazione; si riducono a sistemi dinamici introducendo come
variabili sia la posizione che la velocità. La funzione energia
è conservata oppure dissipata, e le sue proprietà di monotonia
forniscono la funzione di Lyapounov e gli insiemi
invarianti.
Il caso in cui è più semplice costruire una funzione di Lyapounov
è quello del sistema newtoniano ad un grado di libertà, che è un'equazione
differenziale di ordine 2 in ![]() :
:
Si scrive anche ![]() , usando la notazione
, usando la notazione
![]() per indicare la derivata seconda della coordinata
per indicare la derivata seconda della coordinata ![]() ,
ed anche la derivata totale seconda di una qualsiasi funzione di
,
ed anche la derivata totale seconda di una qualsiasi funzione di
![]() :
:
Ponendo ![]() si ottiene un sistema dinamico in
si ottiene un sistema dinamico in ![]() :
:
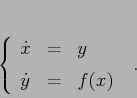
Questi sistemi newtoniani ad un grado di libertà hanno sempre un
integrale primo. Infatti se ![]() è una funzione
è una funzione ![]() :
:
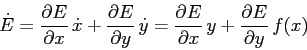
e quindi si ottiene ![]() ponendo, per esempio:
ponendo, per esempio:
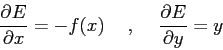
da cui:
I due addendi di ![]() possono essere interpretati come
energia cinetica
(si intende per unità di massa)
possono essere interpretati come
energia cinetica
(si intende per unità di massa) ![]() ed
energia potenziale
ed
energia potenziale
![]() , e quindi
, e quindi ![]() è l'energia totale; il fatto che essa sia costante costituisce
l'integrale dell'energia.
è l'energia totale; il fatto che essa sia costante costituisce
l'integrale dell'energia.
L'energia ![]() è costante su ogni soluzione, e può essere impiegata
per costruire funzioni di Lyapounov:
è costante su ogni soluzione, e può essere impiegata
per costruire funzioni di Lyapounov:
Nel sistema newtoniano ![]() ad un grado di libertà, se
ad un grado di libertà, se
![]() è un punto in cui
è un punto in cui
![]() ha un
minimo locale forte, allora
ha un
minimo locale forte, allora
![]() è
un punto di equilibrio
stabile ma non asintoticamente stabile.
è
un punto di equilibrio
stabile ma non asintoticamente stabile.
Dimostrazione:
allora ![]() è una funzione di Lyapounov per il punto di equilibrio
è una funzione di Lyapounov per il punto di equilibrio
![]() . Infatti
. Infatti ![]() ,
, ![]() ed
ed
![]() in un intorno. Perciò il punto di equilibrio è stabile.
in un intorno. Perciò il punto di equilibrio è stabile.
D'altro canto non può accadere che ![]() sia un punto limite
per
sia un punto limite
per ![]() ; altrimenti si avrebbe su quella soluzione
; altrimenti si avrebbe su quella soluzione ![]() , quindi (essendo
, quindi (essendo ![]() costante sulle soluzioni)
costante sulle soluzioni) ![]() , mentre in
tutti i punti di un intorno di
, mentre in
tutti i punti di un intorno di ![]() (escluso il punto stesso)
si ha
(escluso il punto stesso)
si ha ![]() .
.
Si noti che se il minimo è non degenere, cioè
![]() , allora il sistema linearizzato
in
, allora il sistema linearizzato
in ![]() è del tipo centro:
è del tipo centro:
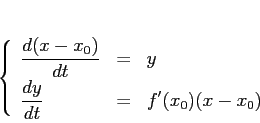
![\begin{displaymath}
A=\left[\begin{array}{cc}{0}&{1}\\
{f'(x_0)}&{0}\end{array}\right] \hspace{5mm},\hspace{5mm}\lambda^2-f'(x_0)=0
\end{displaymath}](img843.png)
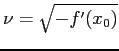 . Dunque gli esponenti di Lyapounov
sono zero, eppure si riesce a dimostrare che il punto di equilibrio
è stabile. Inoltre il teorema di stabilità di Lyapounov si applica
anche al caso di un minimo degenere, con
. Dunque gli esponenti di Lyapounov
sono zero, eppure si riesce a dimostrare che il punto di equilibrio
è stabile. Inoltre il teorema di stabilità di Lyapounov si applica
anche al caso di un minimo degenere, con
Vale il teorema inverso, dimostrato da Cetaev: se ![]() , ma
, ma
![]() non è un punto di minimo locale dell'energia potenziale,
allora
non è un punto di minimo locale dell'energia potenziale,
allora ![]() è un punto di equilibrio instabile. La
dimostrazione è tutt'altro che banale.
è un punto di equilibrio instabile. La
dimostrazione è tutt'altro che banale.
I sistemi newtoniani ad un grado di libertà sono
integrabili in un
senso che sarà precisato nella Sezione 5.2. Il
comportamento qualitativo delle soluzioni, non solo nell'intorno dei
punti di equilibrio stabili ma globalmente, può essere descritto
tracciando le curve di livello della funzione energia nel piano
![]() . Per questo si può utilizzare il metodo grafico seguente:
si disegni il grafico della funzione
. Per questo si può utilizzare il metodo grafico seguente:
si disegni il grafico della funzione ![]() , utilizzando la
conoscenza del segno della sua derivata
, utilizzando la
conoscenza del segno della sua derivata ![]() (attenzione al segno
(attenzione al segno
![]() ).
).
Ad ogni minimo di ![]() , cioè per esempio ad ogni punto
, cioè per esempio ad ogni punto
![]() in cui
in cui ![]() passa da positiva a negativa, corrisponde un punto
di minimo di
passa da positiva a negativa, corrisponde un punto
di minimo di ![]() , quindi un punto di equilibrio stabile del
sistema dinamico. Approssimando
, quindi un punto di equilibrio stabile del
sistema dinamico. Approssimando ![]() con il suo sviluppo di
Taylor, con centro
con il suo sviluppo di
Taylor, con centro ![]() , fino al secondo ordine:
, fino al secondo ordine:
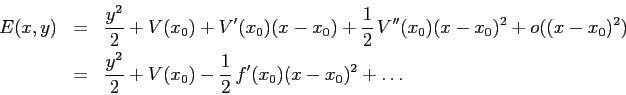
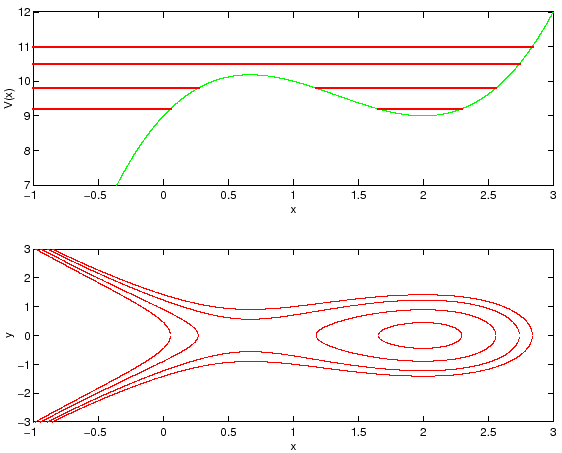
Le curve di livello di ![]() corrispondenti a valori
immediatamente superiori al minimo si chiudono attorno al minimo, come in
Figura 3.1 a destra, approssimativamente
come ellissi:
corrispondenti a valori
immediatamente superiori al minimo si chiudono attorno al minimo, come in
Figura 3.1 a destra, approssimativamente
come ellissi:
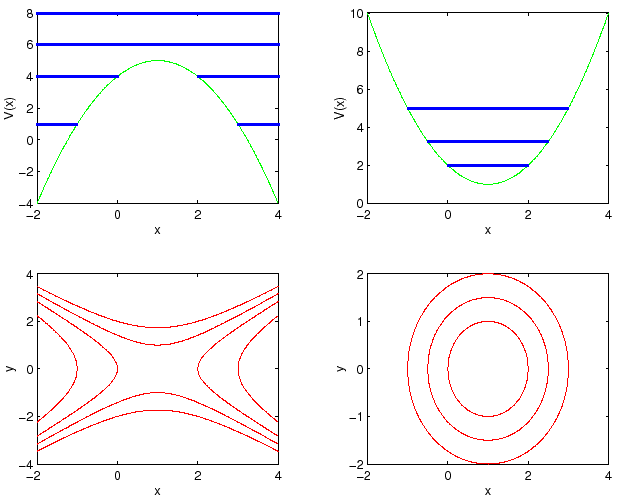 |
Analogamente, ad ogni massimo non degenere di ![]() corrisponde un punto
stazionario di
corrisponde un punto
stazionario di ![]() che non è di estremo ma di sella; le curve
di livello si comportano, in un intorno della sella, come in
Figura 3.1 a sinistra, cioè approssimativamente come le
iperboli
che non è di estremo ma di sella; le curve
di livello si comportano, in un intorno della sella, come in
Figura 3.1 a sinistra, cioè approssimativamente come le
iperboli
Il termine `sella' si usa sia per i punti stazionari delle funzioni di due variabili con matrice hessiana ad autovalori discordi, sia per i punti di equilibrio dei sistemi dinamici il cui linearizzato ha matrice ad autovalori discordi. Per i sistemi newtoniani le due condizioni coincidono, quindi l'uso della stessa parola non genera ambiguità.
Le curve di livello ![]() incrociano la retta
incrociano la retta ![]() nei punti
nei punti
![]() in cui
in cui ![]() , con tangente verticale se
, con tangente verticale se ![]() . Se
invece
. Se
invece ![]() la curva di livello non è regolare in
la curva di livello non è regolare in ![]() ;
se
;
se ![]() è un massimo, si ha un punto di sella a cui arrivano
quattro rami di curva di livello, con due tangenti distinte.
è un massimo, si ha un punto di sella a cui arrivano
quattro rami di curva di livello, con due tangenti distinte.
 |
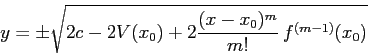
 |
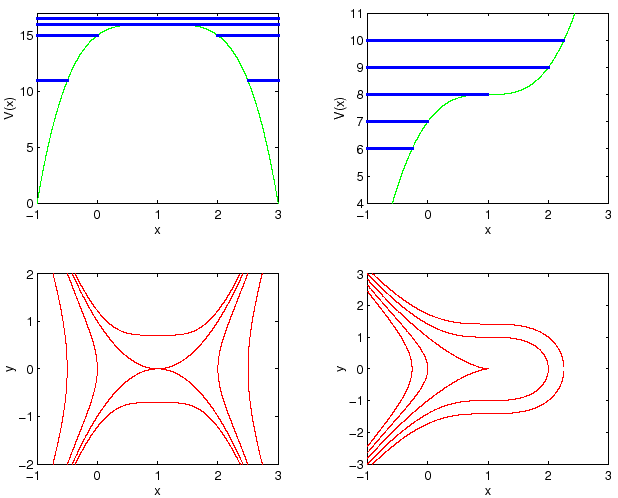
Si possono costruire graficamente in modo globale le curve di livello
![]() tracciando la retta
tracciando la retta ![]() nel piano
nel piano ![]() e facendo
corrispondere ad ogni punto del grafico
e facendo
corrispondere ad ogni punto del grafico ![]() che sta 'sotto'
la retta (
che sta 'sotto'
la retta (![]() ) una coppia di punti nel piano
) una coppia di punti nel piano ![]() con la regola:
con la regola:
In questo modo si ottengono due archi di curva, simmetrici rispetto
alla retta ![]() il cui andamento come grafico
il cui andamento come grafico ![]() rispecchia gli
alti e bassi del grafico
rispecchia gli
alti e bassi del grafico ![]() (al contrario, per
(al contrario, per ![]() ), come in
Figura 3.3.
), come in
Figura 3.3.
Esempio:
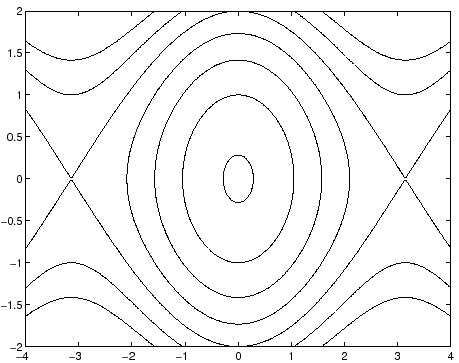 |
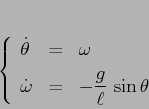
Per studiare globalmente le curve di livello, si traccino per prime
le curve di livello con
![]() , che congiungono
i punti di sella (sono separatrici), come
in Figura 3.4. Le curve di livello con
, che congiungono
i punti di sella (sono separatrici), come
in Figura 3.4. Le curve di livello con
![]() sono curve chiuse che circondano
ciascun equilibrio stabile; per
sono curve chiuse che circondano
ciascun equilibrio stabile; per ![]() si hanno i punti di
minimo, cioè gli equilibri stabili (con il pendolo rivolto verso
il basso). Per
si hanno i punti di
minimo, cioè gli equilibri stabili (con il pendolo rivolto verso
il basso). Per ![]() si ottengono due curve, una contenuta
tutta nel semipiano
si ottengono due curve, una contenuta
tutta nel semipiano ![]() ed una tutta nel semipiano
ed una tutta nel semipiano ![]() .
.
Esercizio
Studiare l'equazione
![]() nei casi
nei casi
Problema
Si descrivano tutti i casi qualitativamente differenti di sistema
newtoniano ![]() in cui
in cui ![]() è un polinomio di terzo grado.
è un polinomio di terzo grado.
Suggerimento:
![]() , possiamo supporre
, possiamo supporre ![]() .
.
Un altro tipo di sistema dinamico per cui la costruzione di una
funzione di Lyapounov è automatica è il
sistema dissipativo a un grado di libertà, che si ottiene aggiungendo
ad un sistema newtoniano un termine di dissipazione, che è funzione
della derivata prima. Per esempio, la dissipazione può essere
costituita da un'accelerazione di segno tale da resistere al moto e di
intensità proporzionale alla velocità: si ottiene così un'equazione differenziale di ordine 2 in ![]() :
:
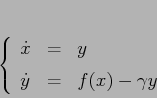
Si utilizza come funzione di Lyapounov la stessa funzione energia del
caso senza dissipazione:
che però non è più un integrale primo:
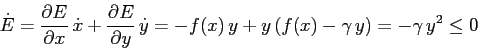
ma è una funzione non crescente sulle orbite.
I punti di equilibrio
sono i punti dell'asse ![]() corrispondenti ai punti stazionari di
corrispondenti ai punti stazionari di
![]() . Se
. Se ![]() è tale che
è tale che ![]() , il sistema linearizzato in
, il sistema linearizzato in
![]() è
è
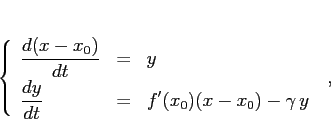
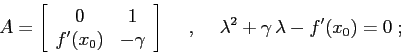
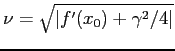 : dunque gli esponenti di Lyapounov
sono negativi, ed il punto di equilibrio è un pozzo, in particolare
asintoticamente stabile.
: dunque gli esponenti di Lyapounov
sono negativi, ed il punto di equilibrio è un pozzo, in particolare
asintoticamente stabile.
Poiché
![]() è una funzione di Lyapounov, il teorema
di stabilità di Lyapounov assicura che i punti di equilibrio
corrispondenti ai minimi di
è una funzione di Lyapounov, il teorema
di stabilità di Lyapounov assicura che i punti di equilibrio
corrispondenti ai minimi di ![]() sono stabili. Questo è vero anche
per i minimi degeneri, a cui non si applica il ragionamento precedente.
sono stabili. Questo è vero anche
per i minimi degeneri, a cui non si applica il ragionamento precedente.
Esempio:
Infatti la soluzione con condizione iniziale ![]() in
in ![]() non può uscire da
non può uscire da ![]() perché
perché ![]() è non crescente;
la soluzione non esce da un compatto e quindi, per il teorema di
continuazione delle soluzioni, è definita per ogni
è non crescente;
la soluzione non esce da un compatto e quindi, per il teorema di
continuazione delle soluzioni, è definita per ogni
![]() .
.
Nei sistemi dissipativi si può facilmente utilizzare il teorema della
funzione di Lyapounov decrescente. Infatti se l'energia
potenziale ![]() ha un minimo (locale forte) in
ha un minimo (locale forte) in ![]() , anche la
funzione energia
, anche la
funzione energia
![]() ha un minimo in
ha un minimo in ![]() ; ne
segue che la componente connessa di
; ne
segue che la componente connessa di ![]() dell'insieme
dell'insieme ![]() , con
, con ![]() un valore appena superiore al minimo, è positivamente
invariante e contiene un solo punto di equilibrio.
un valore appena superiore al minimo, è positivamente
invariante e contiene un solo punto di equilibrio.
La funzione energia
non è una funzione di Lyapounov stretta, infatti
![]() si annulla per
si annulla per ![]() . Quasi tutte le soluzioni attraversano la
retta
. Quasi tutte le soluzioni attraversano la
retta ![]() trasversalmente, cioè con
trasversalmente, cioè con ![]() , e quindi
la funzione
, e quindi
la funzione ![]() ha in questi punti derivata nulla per un
valore isolato di
ha in questi punti derivata nulla per un
valore isolato di ![]() e non cessa di essere decrescente in senso
stretto. Quindi si può applicare il teorema e concludere che tutti i
punti di minimo di
e non cessa di essere decrescente in senso
stretto. Quindi si può applicare il teorema e concludere che tutti i
punti di minimo di ![]() corrispondono a punti di equilibrio
asintoticamente stabili, anche se sono minimi degeneri.
corrispondono a punti di equilibrio
asintoticamente stabili, anche se sono minimi degeneri.
Esempio:
 |
Continuiamo lo studio qualitativo del
pendolo nonlineare con dissipazione
usando il ragionamento precedente. La funzione energia
Per applicare il teorema della
funzione di Lyapounov decrescente
basta far vedere che un insieme ![]() , con
, con ![]() ,
contiene solo orbite su cui
,
contiene solo orbite su cui
![]() è
decrescente. Infatti
è
decrescente. Infatti
![]() si annulla solo per
si annulla solo per
![]() , ma quasi tutte le soluzioni attraversano la retta
, ma quasi tutte le soluzioni attraversano la retta
![]() trasversalmente, con
trasversalmente, con
![]() , e quindi la
funzione
, e quindi la
funzione
![]() ha in questi punti derivata nulla
per un valore isolato di
ha in questi punti derivata nulla
per un valore isolato di ![]() e non cessa di essere decrescente in
senso stretto. Fanno eccezione solo i punti di equilibrio di tipo
sella in
e non cessa di essere decrescente in
senso stretto. Fanno eccezione solo i punti di equilibrio di tipo
sella in
![]() , con
, con ![]() intero. Però i punti di equilibrio di tipo sella sono tali che
intero. Però i punti di equilibrio di tipo sella sono tali che
![]() , quindi sono fuori da
, quindi sono fuori da ![]() per
per ![]() .
.
Ne segue non solo che i punti di equilibrio
![]() con
con ![]() intero sono asintoticamente stabili (questo
era già noto, visto che sono dei pozzi), ma anche che il loro
bacino contiene una componente connessa di
intero sono asintoticamente stabili (questo
era già noto, visto che sono dei pozzi), ma anche che il loro
bacino contiene una componente connessa di
![]() per ogni
per ogni ![]() con
con
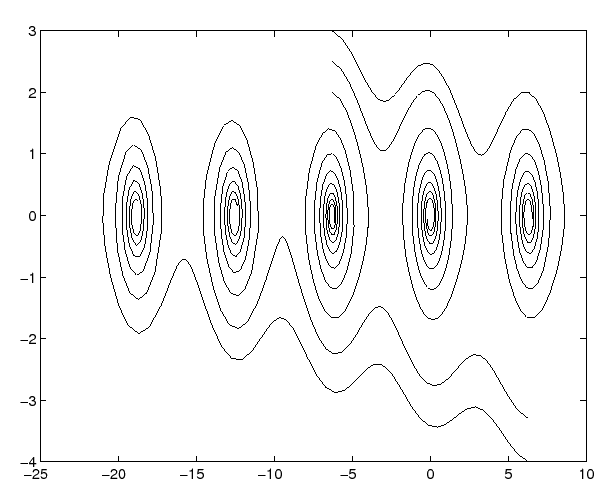
![]() . Se consideriamo degli
insiemi
. Se consideriamo degli
insiemi ![]() con
con ![]() (che sono
connessi), essi sono positivamente
invarianti ma contengono più punti di equilibrio, e quindi si
decompongono nei diversi bacini, come si può vedere nella
Figura 3.5.
(che sono
connessi), essi sono positivamente
invarianti ma contengono più punti di equilibrio, e quindi si
decompongono nei diversi bacini, come si può vedere nella
Figura 3.5.
La frontiera tra i bacini dei diversi pozzi (se li si considera diversi) consiste dei punti sulle separatrici; si veda la Sezione 3.6, e in particolare la Figure 3.10.
Esercizio Dati i sistemi newtoniani con dissipazione
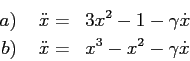
Andrea Milani 2009-06-01