Next: 3.3 FUNZIONI DI LYAPOUNOV Up: 3. TEORIA QUALITATIVA Previous: 3.1 STABILITÀ Indice Indice analitico
Sommario La stabilità o instabilità di un punto di equilibrio
può essere determinata esaminando la sola parte lineare del campo
vettoriale, purché questa non abbia autovalori con parte reale
zero. Infatti la parte lineare dell'equazione differenziale
determina il carattere esponenziale del flusso integrale, e questo
determina il comportamento qualitativo se l'esponente è diverso da
zero.
Definizione:
Se tutti gli esponenti di Lyapounov sono negativi il
punto di equilibrio ![]() si dice un pozzo; se tutti gli
esponenti di Lyapounov sono positivi, il punto di equilibrio
si dice un pozzo; se tutti gli
esponenti di Lyapounov sono positivi, il punto di equilibrio ![]() si dice una sorgente.
si dice una sorgente.
Nel caso di un sistema dinamico continuo lineare, la
stabilità delle soluzioni può essere dedotta dalla loro
espressione in termini di funzioni elementari. Da questo si ricavano
direttamente informazioni sull'andamento delle soluzioni per
![]() .
.
Data la matrice ![]() a coefficienti reali di tipo
a coefficienti reali di tipo ![]() , le due
seguenti proprietà sono equivalenti:
, le due
seguenti proprietà sono equivalenti:
Dimostrazione:
(a)
![]() (b) Se
(b) Se ![]() è una costante positiva tale che
ogni esponente di Lyapounov
è una costante positiva tale che
ogni esponente di Lyapounov ![]() , allora ogni componente della
soluzione tende a zero più rapidamente di
, allora ogni componente della
soluzione tende a zero più rapidamente di ![]() , da cui
segue (b).
, da cui
segue (b).
(b)
![]() (a) Per assurdo: se esiste un esponente di
Lyapounov
(a) Per assurdo: se esiste un esponente di
Lyapounov ![]() , allora la funzione
, allora la funzione
![]() non
tende a zero per
non
tende a zero per ![]() , e qualche componente
di qualche soluzione non tende a zero, in contraddizione con (b).
, e qualche componente
di qualche soluzione non tende a zero, in contraddizione con (b).
Segue dal teorema che l'origine è
asintoticamente stabile
se è un pozzo per il sistema lineare. Invece, se esiste
anche un solo esponente di Lyapounov positivo l'origine è
instabile. Il caso in cui gli esponenti di Lyapounov siano
solamente ![]() (ma non tutti
(ma non tutti ![]() ) non può essere deciso dal
punto di vista della stabilità sulla base dei soli esponenti di
Lyapounov: si possono trovare degli esempi sia stabili che
instabili, come nel caso di risonanza .
) non può essere deciso dal
punto di vista della stabilità sulla base dei soli esponenti di
Lyapounov: si possono trovare degli esempi sia stabili che
instabili, come nel caso di risonanza .
Esempio:
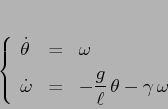
![\begin{displaymath}
A=\left[\begin{array}{cc}{0}&{1}\\
{-g/\ell}&{-\gamma}\en...
...et\,[A-\lambda\,I]= \lambda^2 + \gamma\,\lambda + \frac g\ell
\end{displaymath}](img697.png)
Un teorema del tutto analogo riguarda le sorgenti:
Data la matrice ![]() a coefficienti reali di tipo
a coefficienti reali di tipo ![]() , le due
seguenti proprietà sono equivalenti:
, le due
seguenti proprietà sono equivalenti:
Per estendere la teoria dei pozzi (o sorgenti) al caso nonlineare abbiamo bisogno di una diseguaglianza che deriva dalla teoria della forma canonica di Jordan:
Sia ![]() una matrice a coefficienti reali di tipo
una matrice a coefficienti reali di tipo ![]() , e
siano
, e
siano ![]() due numeri reali tali che per ogni autovalore
due numeri reali tali che per ogni autovalore
![]() di
di ![]()
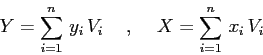
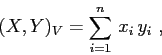
Nel caso in cui ![]() è una matrice semisemplice, la
matrice
è una matrice semisemplice, la
matrice ![]() ha sulla diagonale gli autovalori reali di
ha sulla diagonale gli autovalori reali di ![]() (ciascuno ripetuto un numero di volte pari alla sua
molteplicità algebrica), e
con le coppie di autovalori coniugati rappresentati da un blocco
(ciascuno ripetuto un numero di volte pari alla sua
molteplicità algebrica), e
con le coppie di autovalori coniugati rappresentati da un blocco
![]() (ripetuto per gli autovalori multipli).
La base consiste negli
autovettori
(ripetuto per gli autovalori multipli).
La base consiste negli
autovettori ![]() con autovalori reali
con autovalori reali ![]() , e nelle
coppie
, e nelle
coppie ![]() associate alle coppie di autovalori
associate alle coppie di autovalori
![]() (
(![]() sono la parte reale e la parte complessa di un
autovettore). Allora
sono la parte reale e la parte complessa di un
autovettore). Allora
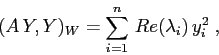
Se la matrice ![]() non è semisemplice, la matrice
non è semisemplice, la matrice ![]() è
diagonale a blocchi con
blocchi di Jordan della
forma
è
diagonale a blocchi con
blocchi di Jordan della
forma ![]() , dove
, dove ![]() ha un solo autovalore reale
ha un solo autovalore reale ![]() oppure una sola coppia di autovalori complessi
oppure una sola coppia di autovalori complessi ![]() , ed
, ed
![]() è in forma canonica dei nilpotenti. Supponiamo che
l'autovalore di un certo blocco
è in forma canonica dei nilpotenti. Supponiamo che
l'autovalore di un certo blocco ![]() sia reale, e siano
sia reale, e siano
![]() i vettori della base relativi ad un tale
blocco. Il fatto che immediatamente sotto la diagonale
principale ci siano dei coefficienti 1 si traduce in:
i vettori della base relativi ad un tale
blocco. Il fatto che immediatamente sotto la diagonale
principale ci siano dei coefficienti 1 si traduce in:
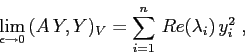
Nel caso nonlineare non si sanno, in generale, esprimere le soluzioni nell'intorno di un punto di equilibrio in forma analitica; in alcuni casi però si possono dedurre le proprietà di stabilità dallo studio del sistema linearizzato.
Sia ![]() un pozzo per il sistema dinamico
un pozzo per il sistema dinamico ![]() ,
definito e
,
definito e ![]() su
su
![]() , e sia
, e sia ![]() la matrice del
sistema linearizzato in
la matrice del
sistema linearizzato in ![]() . Se
. Se ![]() è un numero reale
positivo tale che ogni autovalore
è un numero reale
positivo tale che ogni autovalore ![]() di
di ![]() ha parte reale
ha parte reale
![]() , esiste un intorno
, esiste un intorno ![]() di
di ![]() , (
, (![]() )
tale che:
)
tale che:
La tesi implica che ![]() tende ad
tende ad ![]() per
per ![]() per ogni condizione iniziale
per ogni condizione iniziale ![]() in
in ![]() , in particolare
, in particolare ![]() è asintoticamente stabile.
è asintoticamente stabile.
Dimostrazione:
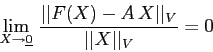
La formula precedente è la definizione di differenziabilità se la norma è la norma euclidea; ma per il teorema di equivalenza delle norme i limiti sono gli stessi.
Per la diseguaglianza di Cauchy
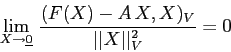
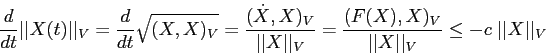
Per dimostrare (a) si ricorre al teorema di continuazione
delle soluzioni: scegliendo nella dimostrazione di (b)
![]() , per ogni
, per ogni ![]() esiste una soluzione
per
esiste una soluzione
per ![]() , che per la disequazione
, che per la disequazione
![]() avrà
avrà
![]() . Considerato il compatto
. Considerato il compatto
![]() , la soluzione può esssere
continuata, ma non può lasciare
, la soluzione può esssere
continuata, ma non può lasciare ![]() , quindi deve essere definita
per ogni
, quindi deve essere definita
per ogni ![]() .
.
Ne segue che gli esponenti di Lyapounov determinano
l'andamento delle soluzioni per ![]() non solo nel caso
lineare. Per un pozzo nonlineare, le soluzioni non sono direttamente
esprimibili mediante funzioni esponenziali ed altre funzioni
analitiche elementari, ma hanno l'andamento asintotico delle
esponenziali.
non solo nel caso
lineare. Per un pozzo nonlineare, le soluzioni non sono direttamente
esprimibili mediante funzioni esponenziali ed altre funzioni
analitiche elementari, ma hanno l'andamento asintotico delle
esponenziali.
Esempio:
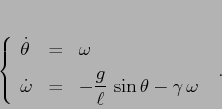
![\begin{displaymath}
A_k=\left[\begin{array}{cc}{0}&{1}\\
{(-1)^{k+1}g/\ell}&{-\gamma}\end{array}\right]
\end{displaymath}](img758.png)
Per poter descrivere il comportamento globale delle orbite di questo sistema dinamico, per esempio mediante un disegno, occorrono informazioni sul comportamento delle soluzioni lontane dai punti di equilibrio. Questo sarà possibile utilizzando il metodo della funzione di Lyapounov.
Esercizio
Consideriamo l'equazione di Van der Pol:
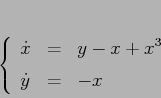
Un teorema del tutto analogo riguarda il caso della sorgente, cioè quello in cui gli esponenti di Lyapounov sono tutti positivi:
Sia ![]() una sorgente per il sistema dinamico
una sorgente per il sistema dinamico ![]() , definito e
, definito e ![]() su
su
![]() , e sia
, e sia ![]() la
matrice del sistema linearizzato in
la
matrice del sistema linearizzato in ![]() .
Se
.
Se ![]() è un numero reale positivo tale che
ogni autovalore
è un numero reale positivo tale che
ogni autovalore ![]() di
di ![]() ha parte reale
ha parte reale
![]() , esiste un intorno
, esiste un intorno ![]() di
di ![]() , (
, (![]() )
tale che:
)
tale che:
Esercizio
Individuare eventuali pozzi e sorgenti del sistema
![\begin{displaymath}
\frac{d\,}{dt} \left[\begin{array}{c}{x}\\
{y}\end{array}\...
...begin{array}{c}{x^2+xy-x}\\
{-xy+y^2-y}\end{array}\right]\;.
\end{displaymath}](img767.png)
Andrea Milani 2009-06-01