Subsections
2.4 AUTOVALORI COMPLESSI
Sommario Se la matrice di un sistema dinamico lineare ha autovalori
complessi, non è diagonalizzabile. Però può essere
diagonalizzabile in campo complesso. Ad ogni coppia di autovalori
complessi coniugati corrisponde un blocco 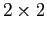 che si può
mettere in una forma canonica. Queste forme canoniche costituiscono un
modello del campo complesso.
che si può
mettere in una forma canonica. Queste forme canoniche costituiscono un
modello del campo complesso.
Tra le matrici a coefficienti reali di tipo 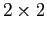 consideriamo il
sottospazio
consideriamo il
sottospazio 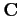 di dimensione 2 delle matrici della forma
di dimensione 2 delle matrici della forma
Il sottospazio 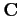 è generato da
è generato da 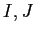 , dove
, dove 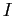 è la matrice
identità e
è la matrice
identità e 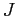 la matrice antisimmetrica definita sopra. In questa
rappresentazione matriciale del numero complesso, la
scelta di
la matrice antisimmetrica definita sopra. In questa
rappresentazione matriciale del numero complesso, la
scelta di 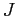 , che determina la struttura complessa, deve
rispettare il requisito
, che determina la struttura complessa, deve
rispettare il requisito 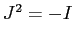 . Ogni
matrice di
. Ogni
matrice di 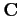 è quindi presentabile in tre forme: come matrice,
come combinazione lineare della base
è quindi presentabile in tre forme: come matrice,
come combinazione lineare della base 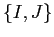 e come coppia di
coordinate rispetto alla base:
e come coppia di
coordinate rispetto alla base:
La forma 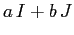 dà la
rappresentazione algebrica del numero complesso;
la forma
dà la
rappresentazione algebrica del numero complesso;
la forma 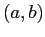 dà la
rappresentazione cartesiana del numero complesso
(nel cosiddetto piano di Argand-Gauss).
dà la
rappresentazione cartesiana del numero complesso
(nel cosiddetto piano di Argand-Gauss).
L'insieme 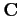 di matrici non solo è chiuso rispetto
all'addizione e alla moltiplicazione per uno scalare, ma anche rispetto
al prodotto di matrici. Infatti
di matrici non solo è chiuso rispetto
all'addizione e alla moltiplicazione per uno scalare, ma anche rispetto
al prodotto di matrici. Infatti
Il fatto più notevole a proposito del prodotto in 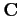 è che
essa gode della proprietà commutativa:
è che
essa gode della proprietà commutativa:
che non vale in generale per le matrici quadrate qualsiasi.
Il generatore 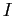 è l'unità reale ed il generatore
è l'unità reale ed il generatore
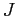 l'unità immaginaria: se
l'unità immaginaria: se 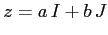 , allora
, allora
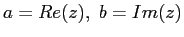 . Il sottospazio di
. Il sottospazio di 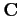 generato da
generato da 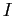 contiene i numeri
complessi che possono essere identificati con i numeri reali,
tramite la corrispondenza biunivoca tra
contiene i numeri
complessi che possono essere identificati con i numeri reali,
tramite la corrispondenza biunivoca tra
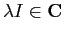 e
e
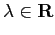 ; si usa perciò dire che
; si usa perciò dire che
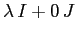 è
un numero reale. Questa identificazione consente anche di scrivere
semplicemente
è
un numero reale. Questa identificazione consente anche di scrivere
semplicemente 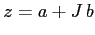 , dove si sottintende l'unità reale.
, dove si sottintende l'unità reale.
L'uso anche contemporaneo delle diverse rappresentazioni dei
numeri complessi è possibile senza contraddizioni. Si possono per
esempio mescolare due modelli di numeri complessi ottenendo una
definizione consistente di prodotto; se infatti 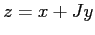 ,
, 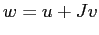 ,
possiamo eseguire il prodotto
,
possiamo eseguire il prodotto 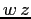 usando per
usando per 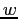 la
rappresentazione come matrice, e la rappresentazione cartesiana
la
rappresentazione come matrice, e la rappresentazione cartesiana
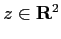 , pur di considerare
, pur di considerare 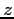 come vettore colonna, ed usando
il prodotto di matrici riga per colonna:
come vettore colonna, ed usando
il prodotto di matrici riga per colonna:
Poiché per ogni matrice di 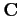 :
:
definiamo, per ogni 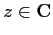 , il modulo di
, il modulo di 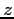 come
come
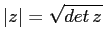 .
Il modulo così definito ha le stesse proprietà della
lunghezza di un vettore:
.
Il modulo così definito ha le stesse proprietà della
lunghezza di un vettore:
In effetti, se consideriamo la forma cartesiana del numero
complesso, cioè 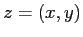 , allora
, allora
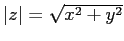 , ossia il
modulo del numero complesso è la lunghezza del vettore che lo
rappresenta nel piano di Argand-Gauss. D'altro canto se
, ossia il
modulo del numero complesso è la lunghezza del vettore che lo
rappresenta nel piano di Argand-Gauss. D'altro canto se 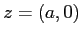 è un numero complesso che è anche reale,
è un numero complesso che è anche reale, 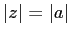 , cioè i tre
usi dello stesso simbolo (e i due della stessa parola ``modulo") non
portano ad alcuna contraddizione.
, cioè i tre
usi dello stesso simbolo (e i due della stessa parola ``modulo") non
portano ad alcuna contraddizione.
Poiché il modulo di un numero complesso è la distanza dall'origine
nel piano di Argand-Gauss, ossia il raggio delle coordinate polari,
vogliamo definire la variabile angolo che assieme ad essa forma le
coordinate polari. Se 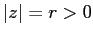 , esiste una ed una sola matrice di
rotazione tale che
, esiste una ed una sola matrice di
rotazione tale che
Infatti
e usando la parametrizzazione della circonferenza 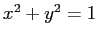 mediante
seno e coseno si ottiene la matrice di rotazione. Allora l'insieme
degli angoli
mediante
seno e coseno si ottiene la matrice di rotazione. Allora l'insieme
degli angoli 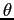 di rotazione della matrice
di rotazione della matrice 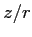 si chiama
argomento del numero complesso
si chiama
argomento del numero complesso 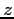 , e si indica con
, e si indica con 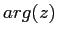 (si
tratta in effetti di una variabile angolo).
(si
tratta in effetti di una variabile angolo).
Il modulo del prodotto è il prodotto dei moduli; gli argomenti
del prodotto sono la somma degli argomenti. Infatti dati 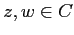
per il teorema del determinante del prodotto. Se poi
con
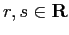 , allora, eseguendo il prodotto
, allora, eseguendo il prodotto
L'ultimo passaggio si può giustificare in due modi: o con
le formule di addizione della trigonometria, o perché
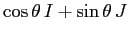 è la matrice associata ad una
rotazione dell'angolo
è la matrice associata ad una
rotazione dell'angolo 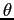 (in verso antiorario),
(in verso antiorario),
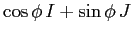 è la matrice associata alla rotazione di
è la matrice associata alla rotazione di 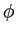 , e
la composizione di due rotazioni è la rotazione dell'angolo somma.
In altre parole, non occorre ricordare le formule di addizione se ci
si ricordano le regole per moltiplicare i numeri complessi (che poi
discendono semplicemente dalle regole
, e
la composizione di due rotazioni è la rotazione dell'angolo somma.
In altre parole, non occorre ricordare le formule di addizione se ci
si ricordano le regole per moltiplicare i numeri complessi (che poi
discendono semplicemente dalle regole
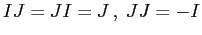 ).
).
Data 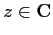 , chiamiamo complesso coniugato di
, chiamiamo complesso coniugato di 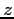 , e
indichiamo con
, e
indichiamo con 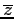 , la matrice trasposta di
, la matrice trasposta di 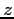 (che è
pure in
(che è
pure in 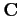 ):
):
Il complesso coniugato ha la stessa parte reale 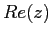 , e parte
immaginaria opposta
, e parte
immaginaria opposta 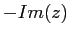 . Ha quindi anche lo stesso modulo
. Ha quindi anche lo stesso modulo 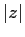 ,
ed argomenti opposti
,
ed argomenti opposti 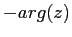 . Vale la proprietà:
. Vale la proprietà:
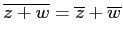 . Anche per il prodotto:
. Anche per il prodotto:
L'inverso di 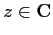 ,
, 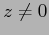 , si può calcolare come
, si può calcolare come
Infatti
Seguono dalla formula dell'inverso le proprietà:
La potenza 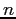 -esima di un numero complesso
-esima di un numero complesso 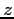 è definita per
induzione nello stesso modo della potenza di un numero reale:
è definita per
induzione nello stesso modo della potenza di un numero reale:
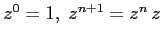 . Usando la formula del modulo del prodotto
e dell'argomento del prodotto si mostra che
. Usando la formula del modulo del prodotto
e dell'argomento del prodotto si mostra che
Le formule del modulo e dell'argomento della potenza
valgono per ogni 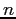 intero, anche negativo, purché naturalmente si
intenda
intero, anche negativo, purché naturalmente si
intenda
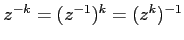 .
.
Sia 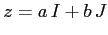 una matrice di
una matrice di 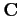 : le radici
dell'equazione caratteristica, cioè i valori di
: le radici
dell'equazione caratteristica, cioè i valori di
 tali che
tali che
sono i numeri complessi 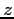 e
e 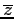 . Infatti sia
. Infatti sia
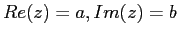 :
:
ha soluzione
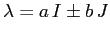 . Questo è un caso
particolare del teorema di Hamilton-Cayley.
. Questo è un caso
particolare del teorema di Hamilton-Cayley.
Consideriamo ora un sistema dinamico lineare con matrice non
diagonalizzabile (in campo reale) di questo tipo:
e costruiamo una variabile complessa 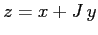 ; poiché come
già osservato si possono mescolare le due rappresentazioni
matriciali e vettoriali, ponendo
; poiché come
già osservato si possono mescolare le due rappresentazioni
matriciali e vettoriali, ponendo 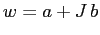 il secondo membro
dell'equazione differenziale si può esprimere come prodotto in
il secondo membro
dell'equazione differenziale si può esprimere come prodotto in 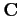 :
:
dove 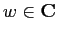 è la stessa cosa di
è la stessa cosa di  considerata come numero complesso;
allora la soluzione si ottiene mediante la
funzione esponenziale di argomento complesso, che è definita dalla serie:
considerata come numero complesso;
allora la soluzione si ottiene mediante la
funzione esponenziale di argomento complesso, che è definita dalla serie:
la cui convergenza è garantita dal teorema di
convergenza in norma, usando il modulo del numero
complesso come norma. Se la condizione iniziale è
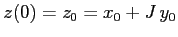 :
:
da cui la soluzione nel senso reale:
L'ambiguità nell'espressione 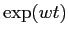 , tra la funzione
esponenziale di una variabile complessa e l'esponenziale di matrice,
non crea alcun problema. In effetti le due serie coincidono e la
loro convergenza può essere dimostrata usando o il
modulo
, tra la funzione
esponenziale di una variabile complessa e l'esponenziale di matrice,
non crea alcun problema. In effetti le due serie coincidono e la
loro convergenza può essere dimostrata usando o il
modulo 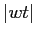 o la norma di matrice
o la norma di matrice 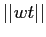 nel teorema di
convergenza in norma.
nel teorema di
convergenza in norma.
Esempio:
Se la matrice 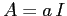 corrisponde ad un numero complesso con
parte immaginaria
corrisponde ad un numero complesso con
parte immaginaria 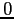 , allora
, allora
e le soluzioni del sistema dinamico sono semplicemente:
Esempio:
Se la matrice  è antisimmetrica
è antisimmetrica
cioè corrisponde ad un numero immaginario puro,
allora le potenze pari sono reali:
mentre le potenze dispari sono antisimmetriche, cioè immaginarie:
perciò le ridotte della serie esponenziale hanno un'espressione
che si può calcolare esplicitamente:
Ora il passaggio da
fare con cautela è il riordino della serie, separando la parte di
grado pari (quindi reale) da quella di grado dispari (quindi
immaginaria). Questo è lecito perché la serie converge
assolutamente, come si deduce dalla convergenza assoluta delle due
serie separate per parte immaginaria e parte reale:
da cui si deduce la formula di Eulero:
Applicando la
formula dell'esponenziale di matrice per descrivere la soluzione del
sistema dinamico in questo caso si ottiene:
e separando parte reale e parte
immaginaria:
cioè la soluzione già nota dell'esempio
dell'oscillatore armonico, con 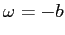 .
.
Per trattare il caso generale dell'equazione 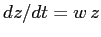 con
con 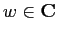 occorre utilizzare il teorema della somma degli esponenti:
poiché le due matrici
occorre utilizzare il teorema della somma degli esponenti:
poiché le due matrici 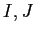 commutano tra loro (
commutano tra loro (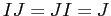 ):
):
e quindi usando i calcoli eseguiti nei due esempi precedenti:
Allora le soluzioni di 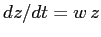 dove
dove
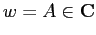 sono le seguenti:
sono le seguenti:
e per ottenere le soluzioni in forma
reale basta moltiplicare ed separare parte reale e parte immaginaria:
Il flusso integrale al tempo 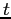 si può descrivere come una rotazione
di un angolo
si può descrivere come una rotazione
di un angolo 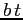 seguita da un'omotetia di un fattore
seguita da un'omotetia di un fattore 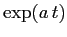 .
.
Vorremmo generalizzare questa soluzione al caso di una arbitraria
matrice  di tipo
di tipo 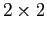 con autovalori complessi coniugati
con autovalori complessi coniugati
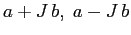 . Consideriamo
. Consideriamo  come operatore lineare su
come operatore lineare su 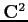 ;
allora esistono in
;
allora esistono in 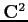 due autovettori:
due autovettori:
Gli autovettori relativi ai due autovalori coniugati
possono essere scelti in modo da essere coniugati tra loro:
 ; infatti,
; infatti,  è reale,
è reale,  e
quindi:
e
quindi:
Consideriamo in 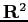 i due vettori
i due vettori
Il simbolo 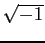 è stato usato al posto di
è stato usato al posto di 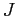 per
evitare confusione tra le operazioni matriciali e le operazioni
algebriche in
per
evitare confusione tra le operazioni matriciali e le operazioni
algebriche in 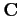 .
Allora riscriviamo le equazioni degli autovalori in termini di
.
Allora riscriviamo le equazioni degli autovalori in termini di 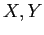 :
:
e separando parte reale e
parte immaginaria:
Supponiamo di usare un sistema di riferimento definito dalla base
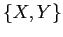 . Verificare che i vettori
. Verificare che i vettori 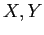 sono
linearmente indipendenti. L'applicazione associata ad
sono
linearmente indipendenti. L'applicazione associata ad  con la base canonica è associata nella nuova base a
con la base canonica è associata nella nuova base a
Perciò se si vuole calcolare
l'esponenziale di matrice di  , si può calcolare
, si può calcolare 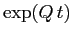 che
è data dalla formula del caso precedente, e poi usare:
che
è data dalla formula del caso precedente, e poi usare:
dove ![$B^{-1}=[X,Y]$](img453.png) ha come colonne i vettori della nuova base.
ha come colonne i vettori della nuova base.
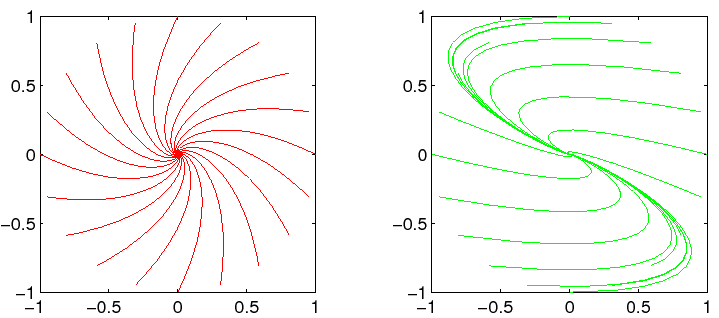
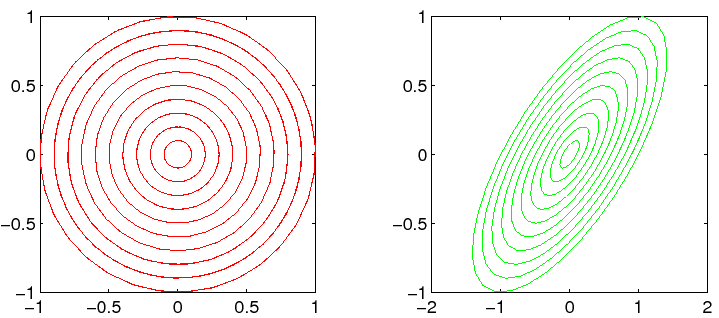
Figura 2.3:
Un punto di equilibrio di tipo fuoco; a sinistra in forma canonica.
 |
In conclusione, se una matrice 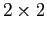 ha autovalori
complessi coniugati, è sempre possibile riportarla con un
cambiamento di riferimento ad una matrice che appartiene a
ha autovalori
complessi coniugati, è sempre possibile riportarla con un
cambiamento di riferimento ad una matrice che appartiene a 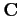 , e
che corrisponde ad uno degli autovalori.
, e
che corrisponde ad uno degli autovalori.
Possiamo quindi studiare il comportamento qualitativo con la
forma canonica
Figura 2.4:
Un punto di equilibrio di tipo centro; a sinistra in forma canonica.
 |
Il comportamento qualitativo delle soluzioni dipende solo dal segno di 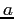 :
:
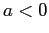 Tutte le orbite (diverse dall'equilibrio) vanno
all'infinito per
Tutte le orbite (diverse dall'equilibrio) vanno
all'infinito per 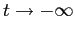 e tendono al
punto di equilibrio nell'origine per
e tendono al
punto di equilibrio nell'origine per
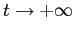 . Le traiettorie sono
delle spirali, che si avvolgono attorno al punto di equilibrio con
frequenza pari alla parte immaginaria
. Le traiettorie sono
delle spirali, che si avvolgono attorno al punto di equilibrio con
frequenza pari alla parte immaginaria 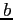 .
.
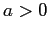 Le orbite tendono al punto di equilibrio per
Le orbite tendono al punto di equilibrio per
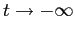 , cioè sono delle spirali che si svolgono. Il punto di
equilibrio si dice di tipo fuoco, sia in questo caso che nel
precedente.
, cioè sono delle spirali che si svolgono. Il punto di
equilibrio si dice di tipo fuoco, sia in questo caso che nel
precedente.
 Tutte le orbite (diverse dall'equilibrio) girano attorno
al punto di equilibrio, ripassando sempre per gli stessi punti: ogni
orbita è quindi un'orbita periodica; i limiti per
Tutte le orbite (diverse dall'equilibrio) girano attorno
al punto di equilibrio, ripassando sempre per gli stessi punti: ogni
orbita è quindi un'orbita periodica; i limiti per
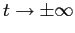 non esistono. Il punto di equilibrio si dice di tipo
centro. Si noti che per
non esistono. Il punto di equilibrio si dice di tipo
centro. Si noti che per 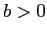 la rotazione attorno al punto di
equilibrio è in senso antiorario, al contrario di quello che si
ottiene nel caso dell'oscillatore armonico. In questo caso
il sistema dinamico ammette un integrale primo
la rotazione attorno al punto di
equilibrio è in senso antiorario, al contrario di quello che si
ottiene nel caso dell'oscillatore armonico. In questo caso
il sistema dinamico ammette un integrale primo
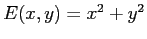 .
.
Problema
Nel piano 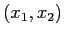 determinare tutte le curve
determinare tutte le curve
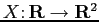 ,
la cui tangente nel punto
,
la cui tangente nel punto 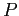 forma un angolo costante
forma un angolo costante 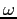 con il
vettore che congiunge l'origine con
con il
vettore che congiunge l'origine con 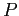 . Per quali
. Per quali 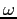 le curve
sono limitate ?
le curve
sono limitate ?
(Soluzione)
Esercizio
Descrivere tutte le soluzioni di 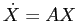 dove
dove
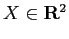 e la matrice
e la matrice
(Soluzione)
Definizione:
Una matrice con tutti gli autovalori, reali o complessi,
semplici (nel senso di molteplicità algebrica 1) è certamente semisemplice, perché
gli autovettori corrispondenti ad autovalori diversi sono sempre
linearmente indipendenti, e per il teorema
fondamentale dell'algebra gli autovalori sono
esattamente 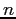 . Però una matrice può essere semisemplice
anche con degli autovalori multipli.
. Però una matrice può essere semisemplice
anche con degli autovalori multipli.
Se la matrice  è semisemplice, allora tutte le orbite del
sistema dinamico:
è semisemplice, allora tutte le orbite del
sistema dinamico:
si possono esprimere mediante combinazioni lineari di funzioni esponenziali
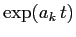 (dove gli
(dove gli 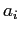 sono le parti reali degli autovalori di
sono le parti reali degli autovalori di  )
moltiplicate per funzioni trigonometriche
)
moltiplicate per funzioni trigonometriche 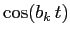 e
e 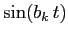 (dove i
(dove i 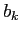 sono le parti immaginarie degli autovalori di
sono le parti immaginarie degli autovalori di  ).
).
Dimostrazione:
L'equazione caratteristica
![$det\,[A-\lambda\, I]=0$](img474.png) è
un'equazione algebrica, di grado
è
un'equazione algebrica, di grado 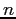 se
se  è di tipo
è di tipo 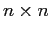 ,
a coefficienti reali che sono gli invarianti della matrice.
Perciò essa ha
,
a coefficienti reali che sono gli invarianti della matrice.
Perciò essa ha 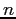 radici, contate con la loro molteplicità, tra cui
alcune reali
radici, contate con la loro molteplicità, tra cui
alcune reali
e altre a coppie complesse coniugate:
Anche se alcune radici sono ripetute, per ipotesi  è
semisemplice e quindi per ogni autovalore c'è un autovettore, in
modo che ce ne siano
è
semisemplice e quindi per ogni autovalore c'è un autovettore, in
modo che ce ne siano 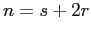 tra loro linearmente indipendenti.
Perciò per gli autovalori reali:
tra loro linearmente indipendenti.
Perciò per gli autovalori reali:
e per quelli complessi:
dove gli autovettori relativi a due autovalori
complessi coniugati possono essere scelti in modo da essere
coniugati tra loro:
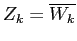 , per lo stesso ragionamento
fatto sopra nel caso di una sola coppia.
Sarebbe necessario verificare
che questa scelta mantiene l'indipendenza lineare su
, per lo stesso ragionamento
fatto sopra nel caso di una sola coppia.
Sarebbe necessario verificare
che questa scelta mantiene l'indipendenza lineare su 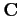 degli
autovettori.
Prendiamo ora una base di
degli
autovettori.
Prendiamo ora una base di 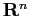 costituita dai
seguenti vettori reali:
costituita dai
seguenti vettori reali:
Sarebbe necessario verificare che questa è una base; per esempio la
parte reale del sottospazio generato da
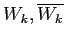 è
generata da
è
generata da
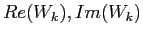 .
.
Scriviamo la matrice 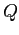 che esprime la stessa applicazione lineare di
che esprime la stessa applicazione lineare di
 , rispetto alla base così definita. Nella nuova base
, rispetto alla base così definita. Nella nuova base
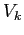 è espresso in componenti come il vettore
è espresso in componenti come il vettore 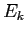 della base canonica
(con tutte le componenti
della base canonica
(con tutte le componenti 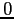 salvo la
salvo la 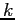 -esima uguale a
-esima uguale a 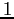 ):
):
da cui si deduce che le prime 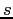 colonne della matrice
colonne della matrice 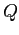 sono
quelle di una matrice diagonale, con gli autovalori reali sulla
diagonale principale.
sono
quelle di una matrice diagonale, con gli autovalori reali sulla
diagonale principale.
Consideriamo ora la coppia di vettori
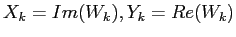 che
compaiono nella base al posto
che
compaiono nella base al posto 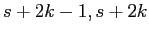 , e perciò sono
rappresentati in componenti nel nuovo sistema di riferimento da
, e perciò sono
rappresentati in componenti nel nuovo sistema di riferimento da
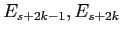 : ripetendo lo stesso ragionamento del caso
con una sola coppia di autovalori coniugati:
: ripetendo lo stesso ragionamento del caso
con una sola coppia di autovalori coniugati:
e quindi la matrice 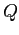 del nuovo sistema di riferimento ha questo
effetto:
del nuovo sistema di riferimento ha questo
effetto:
il che vuol dire che nelle colonne 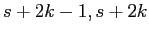 della matrice
della matrice
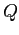 i coefficienti sono tutti zero salvo quelli della sottomatrice
i coefficienti sono tutti zero salvo quelli della sottomatrice
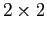 vicino alla diagonale, che è:
vicino alla diagonale, che è:
Per ogni coppia di autovalori complessi coniugati, nella
matrice trasformata al nuovo sistema di riferimento appare un
blocco 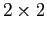 che è in
che è in 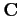 , e corrisponde ad uno dei due
autovalori in questione.
, e corrisponde ad uno dei due
autovalori in questione.
In conclusione la matrice  può
essere trasformata per coniugio nella matrice
può
essere trasformata per coniugio nella matrice
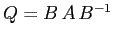 dove
la matrice
dove
la matrice 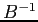 è formata dai vettori colonna della nuova
base; la matrice
è formata dai vettori colonna della nuova
base; la matrice 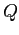 ha sulla diagonale principale gli autovalori
reali e in blocchi
ha sulla diagonale principale gli autovalori
reali e in blocchi 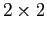 vicino alla diagonale principale gli
autovalori complessi. Esprimiamo questa forma speciale della matrice
vicino alla diagonale principale gli
autovalori complessi. Esprimiamo questa forma speciale della matrice 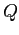 con la notazione diagonale a blocchi:
con la notazione diagonale a blocchi:
con la convenzione che ogni autovalore complesso
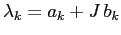 sia descritto dal suo blocco
sia descritto dal suo blocco 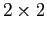 .
Una matrice
.
Una matrice 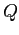 di questa forma si chiama
forma canonica di un semisemplice.
L'esponenziale
di questa forma si chiama
forma canonica di un semisemplice.
L'esponenziale 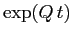 sarà diagonale a blocchi, cioè data da un'espressione
analoga a quella dell'esponenziale di una matrice
diagonale:
sarà diagonale a blocchi, cioè data da un'espressione
analoga a quella dell'esponenziale di una matrice
diagonale:
dove l'esponenziale di un numero reale è la funzione
esponenziale, e l'esponenziale di un numero complesso è
rappresentata da una matrice 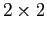 :
:
La dimostrazione è conclusa con l'esame della formula usuale:
C.D.D.
Esercizio
Determinare il flusso integrale del sistema dinamico
e determinare quali orbite hanno  come limite per
come limite per 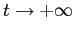 , quali per
, quali per 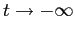 .
.
(Soluzione)
Andrea Milani
2009-06-01
![]() che si può
mettere in una forma canonica. Queste forme canoniche costituiscono un
modello del campo complesso.
che si può
mettere in una forma canonica. Queste forme canoniche costituiscono un
modello del campo complesso. ![]() consideriamo il
sottospazio
consideriamo il
sottospazio ![]() di dimensione 2 delle matrici della forma
di dimensione 2 delle matrici della forma
![\begin{displaymath}
\left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\end{array}\right...
...array}{cc}{0}&{-1}\\
{1}&{0}\end{array}\right] = a\,I + b\,J
\end{displaymath}](img337.png)
![]() è generato da
è generato da ![]() , dove
, dove ![]() è la matrice
identità e
è la matrice
identità e ![]() la matrice antisimmetrica definita sopra. In questa
rappresentazione matriciale del numero complesso, la
scelta di
la matrice antisimmetrica definita sopra. In questa
rappresentazione matriciale del numero complesso, la
scelta di ![]() , che determina la struttura complessa, deve
rispettare il requisito
, che determina la struttura complessa, deve
rispettare il requisito ![]() . Ogni
matrice di
. Ogni
matrice di ![]() è quindi presentabile in tre forme: come matrice,
come combinazione lineare della base
è quindi presentabile in tre forme: come matrice,
come combinazione lineare della base ![]() e come coppia di
coordinate rispetto alla base:
e come coppia di
coordinate rispetto alla base:
![\begin{displaymath}
\left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\end{array}\right] = a\,I + b\, J \simeq (a,b)
\end{displaymath}](img341.png)
![]() di matrici non solo è chiuso rispetto
all'addizione e alla moltiplicazione per uno scalare, ma anche rispetto
al prodotto di matrici. Infatti
di matrici non solo è chiuso rispetto
all'addizione e alla moltiplicazione per uno scalare, ma anche rispetto
al prodotto di matrici. Infatti
![\begin{displaymath}
\left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\end{array}\right...
...&{-(ad+bc)}\\
{bc+ad}&{-bd+ac}\end{array}\right] \in {\bf C}
\end{displaymath}](img344.png)
![]() è che
essa gode della proprietà commutativa:
è che
essa gode della proprietà commutativa:
![]() è l'unità reale ed il generatore
è l'unità reale ed il generatore
![]() l'unità immaginaria: se
l'unità immaginaria: se ![]() , allora
, allora
![]() . Il sottospazio di
. Il sottospazio di ![]() generato da
generato da ![]() contiene i numeri
complessi che possono essere identificati con i numeri reali,
tramite la corrispondenza biunivoca tra
contiene i numeri
complessi che possono essere identificati con i numeri reali,
tramite la corrispondenza biunivoca tra
![]() e
e
![]() ; si usa perciò dire che
; si usa perciò dire che
![]() è
un numero reale. Questa identificazione consente anche di scrivere
semplicemente
è
un numero reale. Questa identificazione consente anche di scrivere
semplicemente ![]() , dove si sottintende l'unità reale.
, dove si sottintende l'unità reale.
![]() ,
, ![]() ,
possiamo eseguire il prodotto
,
possiamo eseguire il prodotto ![]() usando per
usando per ![]() la
rappresentazione come matrice, e la rappresentazione cartesiana
la
rappresentazione come matrice, e la rappresentazione cartesiana
![]() , pur di considerare
, pur di considerare ![]() come vettore colonna, ed usando
il prodotto di matrici riga per colonna:
come vettore colonna, ed usando
il prodotto di matrici riga per colonna:
![\begin{displaymath}
w\,z=\left[\begin{array}{cc}{u}&{-v}\\
{v}&{u}\end{array}\...
...t]=\left[\begin{array}{c}{ux-vy}\\
{vx+uy}\end{array}\right]
\end{displaymath}](img358.png)
![]() :
:
![\begin{displaymath}
det\, \left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\end{array}\right]=a^2+b^2 \geq 0
\end{displaymath}](img359.png)
![]() , esiste una ed una sola matrice di
rotazione tale che
, esiste una ed una sola matrice di
rotazione tale che
![\begin{displaymath}
z=r\, \left[\begin{array}{cc}{\cos\theta}&{-\sin\theta}\\
{\sin\theta}&{\cos\theta}\end{array}\right]
\end{displaymath}](img368.png)
![\begin{displaymath}
z/r= \left[\begin{array}{cc}{x}&{-y}\\
{y}&{x}\end{array}\right] \ \ con \ \ x^2+y^2=1
\end{displaymath}](img369.png)
![]()
![]() , chiamiamo complesso coniugato di
, chiamiamo complesso coniugato di ![]() , e
indichiamo con
, e
indichiamo con ![]() , la matrice trasposta di
, la matrice trasposta di ![]() (che è
pure in
(che è
pure in ![]() ):
):
![\begin{displaymath}z=\left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\end{array}\right] = a\,I+b\,J\simeq (a,b)\end{displaymath}](img384.png)
![\begin{displaymath}\overline z = {\left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\en...
...a}&{b}\\
{-b}&{a}\end{array}\right] =
a\,I-b\,J\simeq (a,-b)\end{displaymath}](img385.png)
![]() ,
, ![]() , si può calcolare come
, si può calcolare come
![\begin{displaymath}
z^{-1}={\left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\end{arra...
...{a}\end{array}\right]}^T = \frac 1{\vert z\vert^2}
\overline z
\end{displaymath}](img394.png)
![]() una matrice di
una matrice di ![]() : le radici
dell'equazione caratteristica, cioè i valori di
: le radici
dell'equazione caratteristica, cioè i valori di
![]() tali che
tali che
![\begin{displaymath}
det\,[z-\lambda I]=det\;\left[\begin{array}{cc}{a-\lambda}&{-b}\\
{b}&{a-\lambda}\end{array}\right]
=(a-\lambda)^2 + b^2=0
\end{displaymath}](img402.png)
![\begin{displaymath}
\left[\begin{array}{c}{\dot x}\\
{\dot y}\end{array}\right...
...}\right]\; \left[\begin{array}{c}{x}\\
{y}\end{array}\right]
\end{displaymath}](img404.png)
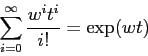
![]() , tra la funzione
esponenziale di una variabile complessa e l'esponenziale di matrice,
non crea alcun problema. In effetti le due serie coincidono e la
loro convergenza può essere dimostrata usando o il
modulo
, tra la funzione
esponenziale di una variabile complessa e l'esponenziale di matrice,
non crea alcun problema. In effetti le due serie coincidono e la
loro convergenza può essere dimostrata usando o il
modulo ![]() o la norma di matrice
o la norma di matrice ![]() nel teorema di
convergenza in norma.
nel teorema di
convergenza in norma.
![\begin{displaymath}
A=\left[\begin{array}{cc}{0}&{-b}\\
{b}&{0}\end{array}\right]=b\,J ,\end{displaymath}](img420.png)
![\begin{displaymath}\sum_{k=0}^{2s+1} \frac{A^kt^k}{k!} = \sum_{m=0}^s\left[
\fr...
...^m}{(2m+1)!}\, J +
\frac{b^{2m}t^{2m}(-1)^m}{(2m)!} \,I\right]\end{displaymath}](img423.png)
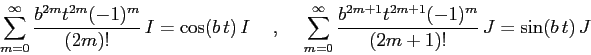
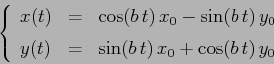
![]() con
con ![]() occorre utilizzare il teorema della somma degli esponenti:
poiché le due matrici
occorre utilizzare il teorema della somma degli esponenti:
poiché le due matrici ![]() commutano tra loro (
commutano tra loro (![]() ):
):
![\begin{displaymath}\left\{\begin{array}{lcl}
{\displaystyle x(t)} & {\display...
...,t}\, [\sin(b\,t)\, x_0 +\cos(b\,t)\,y_0]}
\end{array}\right.
\end{displaymath}](img435.png)
![]() di tipo
di tipo ![]() con autovalori complessi coniugati
con autovalori complessi coniugati
![]() . Consideriamo
. Consideriamo ![]() come operatore lineare su
come operatore lineare su ![]() ;
allora esistono in
;
allora esistono in ![]() due autovettori:
due autovettori:
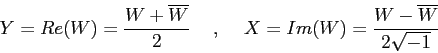
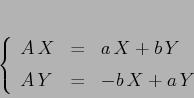
![\begin{displaymath}
Q=\left[\begin{array}{cc}{a}&{-b}\\
{b}&{a}\end{array}\right]= a\, I + b\,J
\end{displaymath}](img450.png)
![]() ha autovalori
complessi coniugati, è sempre possibile riportarla con un
cambiamento di riferimento ad una matrice che appartiene a
ha autovalori
complessi coniugati, è sempre possibile riportarla con un
cambiamento di riferimento ad una matrice che appartiene a ![]() , e
che corrisponde ad uno degli autovalori.
, e
che corrisponde ad uno degli autovalori.
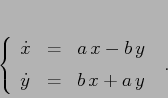
![]() :
:
![]() determinare tutte le curve
determinare tutte le curve
![]() ,
la cui tangente nel punto
,
la cui tangente nel punto ![]() forma un angolo costante
forma un angolo costante ![]() con il
vettore che congiunge l'origine con
con il
vettore che congiunge l'origine con ![]() . Per quali
. Per quali ![]() le curve
sono limitate ?
le curve
sono limitate ?
![]() dove
dove
![]() e la matrice
e la matrice
![\begin{displaymath}
A=\left[\begin{array}{cc}{2}&{-3}\\
{2}&{\phantom{-}2}\end{array}\right] \ .
\end{displaymath}](img465.png)
![]() . Però una matrice può essere semisemplice
anche con degli autovalori multipli.
. Però una matrice può essere semisemplice
anche con degli autovalori multipli.
![]() è semisemplice, allora tutte le orbite del
sistema dinamico:
è semisemplice, allora tutte le orbite del
sistema dinamico:
![]() che esprime la stessa applicazione lineare di
che esprime la stessa applicazione lineare di
![]() , rispetto alla base così definita. Nella nuova base
, rispetto alla base così definita. Nella nuova base
![]() è espresso in componenti come il vettore
è espresso in componenti come il vettore ![]() della base canonica
(con tutte le componenti
della base canonica
(con tutte le componenti ![]() salvo la
salvo la ![]() -esima uguale a
-esima uguale a ![]() ):
):
![]() che
compaiono nella base al posto
che
compaiono nella base al posto ![]() , e perciò sono
rappresentati in componenti nel nuovo sistema di riferimento da
, e perciò sono
rappresentati in componenti nel nuovo sistema di riferimento da
![]() : ripetendo lo stesso ragionamento del caso
con una sola coppia di autovalori coniugati:
: ripetendo lo stesso ragionamento del caso
con una sola coppia di autovalori coniugati:
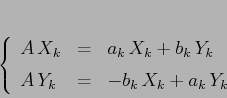
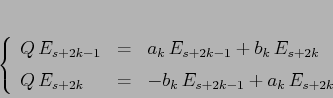
![\begin{displaymath}\left[\begin{array}{cc}{q_{s+2k-1,s+2k-1}}&{q_{s+2k-1,s+2k}}\...
...\begin{array}{cc}{a_k}&{-b_k}\\
{b_k}&{a_k}\end{array}\right]\end{displaymath}](img493.png)
![]() che è in
che è in ![]() , e corrisponde ad uno dei due
autovalori in questione.
, e corrisponde ad uno dei due
autovalori in questione.
![]() può
essere trasformata per coniugio nella matrice
può
essere trasformata per coniugio nella matrice
![]() dove
la matrice
dove
la matrice ![]() è formata dai vettori colonna della nuova
base; la matrice
è formata dai vettori colonna della nuova
base; la matrice ![]() ha sulla diagonale principale gli autovalori
reali e in blocchi
ha sulla diagonale principale gli autovalori
reali e in blocchi ![]() vicino alla diagonale principale gli
autovalori complessi. Esprimiamo questa forma speciale della matrice
vicino alla diagonale principale gli
autovalori complessi. Esprimiamo questa forma speciale della matrice ![]() con la notazione diagonale a blocchi:
con la notazione diagonale a blocchi:
![\begin{displaymath}\begin{array}{l}
\exp(diag\, [ c_1,\ldots, c_s, \lambda_1,\l...
...),
\exp(\lambda_1\,t),\ldots,\exp(\lambda_r\, t)]
\end{array}\end{displaymath}](img498.png)
![\begin{displaymath}
\exp(c_k\,t)=e^{c_k\,t}\hspace{5mm},\hspace{5mm}\exp(a_k\,t...
...(b_k\,t)}\\
{\sin(b_k\,t)}&{\cos(b_k\,t)}\end{array}\right]
\end{displaymath}](img499.png)
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle \frac{d\,X}{dt}}...
...}
{3}&{1}&{-4}\\ {3}&{4}&{-3}\\ {-1}&{4}&{0}\end{array}\right]
\end{displaymath}](img501.png)