Next: 1.4 NOTAZIONI E INDICI Up: 1. DEFINIZIONI E PRIMI Previous: 1.2 SISTEMI LINEARI, INTEGRABILITÀ Indice Indice analitico
Sommario Alcuni sistemi dinamici continui hanno degli invarianti,
che si conservano ``lungo'' le soluzioni, al variare del
tempo nel flusso integrale. Una funzione che si conserva al passare
del tempo è un integrale primo. Altri invarianti sono esprimibili
mediante integrali, per esempio l'area. Definizioni analoghe si
applicano anche al caso discreto.
![\begin{displaymath}\left[\begin{array}{c}{x(t)}\\
{y(t)}\end{array}\right]= \l...
...ight] \left[\begin{array}{c}{x_0}\\
{y_0}\end{array}\right]
\end{displaymath}](img147.png)
Definizione:
Ogni insieme di livello di ![]() è un insieme
invariante.
è un insieme
invariante.
Esempio:
Calcolando la
derivata totale, cioè la derivata di ![]() lungo una soluzione
lungo una soluzione
![]() con la formula usuale di derivazione delle funzioni
composte:
con la formula usuale di derivazione delle funzioni
composte:
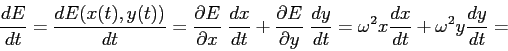
Definizione:
Esempio:
Definizione:
Esempio:
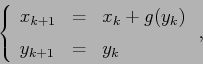
Definizione:
Esempio:
Si noti che ci sono due casi possibili, qualitativamente molto
diversi tra loro: nel primo ![]() è una matrice di rotazione, che
ha automaticamente determinante 1, nel secondo:
è una matrice di rotazione, che
ha automaticamente determinante 1, nel secondo:
![\begin{displaymath}
A=\left[\begin{array}{cc}{\lambda}&{0}\\
{0}&{1/\lambda}\end{array}\right]\end{displaymath}](img170.png)
Andrea Milani 2009-06-01