Next: 4.4 METODI DI INTEGRAZIONE Up: 4. DISCRETIZZAZIONE Previous: 4.2 METODO DI EULERO Indice Indice analitico
Sommario Equazioni differenziali di ordine superiore possono essere
discretizzate utilizzando diverse approssimazioni per le derivate non
solo prime ma anche di ordine superiore. Alcune di queste
approssimazioni, come quella che è equivalente al metodo
di Eulero, hanno però delle proprietà qualitative indesiderabili,
per esempio modificano le proprietà di stabilità delle soluzioni.
Altre approssimazioni sono conservative, cioè se applicate ad un
sistema dinamico continuo conservativo producono un sistema dinamico
discreto ugualmente conservativo. Non esiste però un metodo che consenta
di preservare sempre gli integrali primi del sistema continuo, quindi
le discretizzazioni vanno sempre interpretate come approssimazioni
anche nel senso qualitativo, perché riproducono in modo
imperfetto proprietà qualitative come
l'integrabilità.
Per approssimare le soluzioni di un'equazione differenziale di ordine
superiore al primo con un sistema dinamico discreto si possono seguire
due approcci: il più semplice è quello di ridursi ad un sistema
dinamico e poi usare una discretizzazione per quest'ultimo, per
esempio il metodo di Eulero
![]() (oppure altri più
accurati come sarà descritto nella Sezione 4.4).
(oppure altri più
accurati come sarà descritto nella Sezione 4.4).
Può essere più conveniente tentare di scrivere direttamente una formula di approssimazione per le derivate di ordine superiore. Queste approssimazioni possono essere scritte in termini di un'algebra di operatori.
Definizione:
Segue immediatamente dalle proprietà di commutazione che si può
applicare la formula del binomio di Newton per calcolare le
potenze di ![]() : la differenza k-esima in avanti è
: la differenza k-esima in avanti è
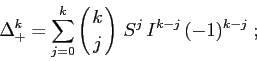
Queste formule possono essere impiegate direttamente in
approssimazioni discrete delle derivate di ordine superiore, del tipo
Esempio:
Si ottiene l'equazione alle differenze finite lineare del secondo ordine
![\begin{displaymath}
x_{k+2}=2x_{k+1}+ \left(-1-\omega^2\,h^2\right)\,x_k
\Longle...
...A\;\left[\begin{array}{c}{x_k}\\
{x_{k+1}}\end{array}\right]
\end{displaymath}](img1337.png)
![\begin{displaymath}
A=\left[\begin{array}{cc}{0}&{1}\\
{-1-\omega^2\,h^2}&{2}\end{array}\right]\;,
\end{displaymath}](img1338.png)
La matrice ![]() può essere scritta nella forma canonica
può essere scritta nella forma canonica
![\begin{displaymath}
B=\left[\begin{array}{cc}{1}&{\omega\,h}\\
{-\omega\,h}&{1}\end{array}\right]\;.
\end{displaymath}](img1341.png)
![\begin{displaymath}
\left[\begin{array}{c}{x_k}\\
{x_{k+1}}\end{array}\right] ...
...gin{array}{cc}{1}&{0}\\
{1}&{\omega\,h}\end{array}\right]\;.
\end{displaymath}](img1347.png)
Esercizio
Se si usasse una discretizzazione basata sulla
differenza all'indietro:
Per equazioni differenziali che contengono solo le derivate di ordine pari si può trovare un procedimento di approssimazione che ha proprietà molto migliori, in particolare che non introduce moltiplicatori di Lyapounov spurii come il metodo di Eulero.
Definizione:
Usando le regole di commutazione e il binomio di Newton si
verifica che le potenze pari di ![]() non usano ``mezzi
passi'', quindi sono definite come operatori su di una successione;
per esempio,
non usano ``mezzi
passi'', quindi sono definite come operatori su di una successione;
per esempio,
Le differenze centrali sono quindi utili per definire una
discretizzazione di equazioni senza derivate di ordine dispari,
per esempio usando
Esempio:
![\begin{displaymath}
\left[\begin{array}{c}{x_k}\\
{x_{k+1}}\end{array}\right]...
...y}{cc}{0}&{1}\\
{-1}&{2-\omega^2\,h^2}\end{array}\right]\;,
\end{displaymath}](img1355.png)
![\begin{displaymath}
\left[\begin{array}{c}{x_k}\\
{x_{k+1}}\end{array}\right]...
... \left[\begin{array}{c}{x_0}\\
{x_1}\end{array}\right] \;,
\end{displaymath}](img1360.png)
dove la matrice ![]() ha per colonne la parte reale e la parte
complessa di un autovettore di autovalore
ha per colonne la parte reale e la parte
complessa di un autovettore di autovalore ![]() , ed
, ed
![]() è una matrice di rotazione, con l'angolo di
rotazione ad ogni passo dato da
è una matrice di rotazione, con l'angolo di
rotazione ad ogni passo dato da
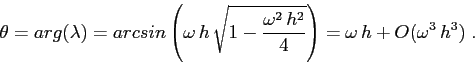
L'esempio qua sopra mostra che, nel caso di un sistema dinamico
continuo dotato di due proprietà importanti come quella di essere
conservativo e di avere un integrale primo, è
talvolta possibile costruire una approssimazione discreta che mantiene
entrambe le proprietà: infatti le rotazioni ![]() che
descrivono la soluzione del sistema discreto conservano l'area, e
lasciano invariata la funzione energia. Queste proprietà però sono
valide solo in un certo sistema di coordinate, definito dal
cambiamento di coordinate
che
descrivono la soluzione del sistema discreto conservano l'area, e
lasciano invariata la funzione energia. Queste proprietà però sono
valide solo in un certo sistema di coordinate, definito dal
cambiamento di coordinate ![]() . Inoltre il problema è capire se
queste due proprietà possono essere conservate anche in casi non
banali, nei quali la soluzione del sistema dinamico continuo non è
nota esplicitamente.
. Inoltre il problema è capire se
queste due proprietà possono essere conservate anche in casi non
banali, nei quali la soluzione del sistema dinamico continuo non è
nota esplicitamente.
Vogliamo generalizzare l'esempio precedente al caso di un qualsiasi
sistema newtoniano ad un grado di libertà:
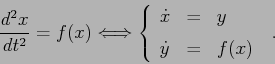
Se usiamo le differenze centrali otteniamo la discretizzazione
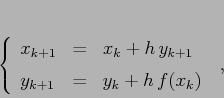
La mappa standard associata a ![]() , con
, con ![]() di classe
di classe ![]() su un aperto
su un aperto
![]() , è conservativa su
, è conservativa su
![]() .
Dimostrazione:
.
Dimostrazione:
![\begin{displaymath}
\left[\begin{array}{c}{x_k}\\
{y_k}\end{array}\right]\long...
...t[\begin{array}{c}{x_{k+1}}\\
{y_{k+1}}\end{array}\right]\;,
\end{displaymath}](img1378.png)
![\begin{displaymath}
\left[\begin{array}{c}{x}\\
{y}\end{array}\right]\longmapsto \left[\begin{array}{c}{x}\\
{y+a(x)}\end{array}\right]
\end{displaymath}](img1379.png)
![\begin{displaymath}
\left[\begin{array}{c}{x}\\
{y}\end{array}\right]\longmapsto \left[\begin{array}{c}{x+b(y)}\\
{y}\end{array}\right]\;,
\end{displaymath}](img1380.png)
Ogni scorrimento è un
sistema dinamico discreto conservativo:
infatti una mappa conserva l'area se e solo se il
determinante jacobiano della trasformazione vale ovunque ![]() (segue dal teorema del
cambiamento di variabili negli integrali doppi).
Nei due casi la matrice jacobiana è
(segue dal teorema del
cambiamento di variabili negli integrali doppi).
Nei due casi la matrice jacobiana è
![\begin{displaymath}
\frac{\partial {(x,y+a(x))}}{\partial {(x,y)}}=\left[\begin{...
...[\begin{array}{cc}{1}&{b'(y)}\\
{0}&{1}\end{array}\right]\;,
\end{displaymath}](img1382.png)
 |
In conclusione la mappa standard costituisce una discretizzazione conservativa, che trasforma un sistema dinamico continuo conservativo in un sistema discreto pure conservativo. Però la risposta al quesito se la mappa standard abbia un integrale primo (analogo all'integrale dell'energia del sistema continuo) è negativa. Per mostrare questo è sufficiente un controesempio:
Esempio:
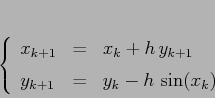
Ricordarsi di calcolare prima la seconda equazione e poi la prima.
 |
 |
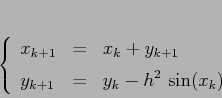
La mappa standard del pendolo dipende quindi da un solo parametro
![]() . Intuitivamente è chiaro che per
. Intuitivamente è chiaro che per ![]() molto piccolo
il sistema discreto approssimerà il sistema continuo, e quindi la
funzione energia
molto piccolo
il sistema discreto approssimerà il sistema continuo, e quindi la
funzione energia
![]() cambierà di poco ad ogni
passo, e la successione
cambierà di poco ad ogni
passo, e la successione ![]() si muoverà quasi lungo le curve
di livello di
si muoverà quasi lungo le curve
di livello di ![]() , cioè vicino alla soluzione del sistema
continuo. Invece per
, cioè vicino alla soluzione del sistema
continuo. Invece per ![]() grande il sistema discreto non avrà
niente a che fare con il sistema continuo: per
grande il sistema discreto non avrà
niente a che fare con il sistema continuo: per ![]() nell'origine diventa una mappa instabile, come risulta
dall'analisi della discretizzazione del pendolo lineare.
nell'origine diventa una mappa instabile, come risulta
dall'analisi della discretizzazione del pendolo lineare.
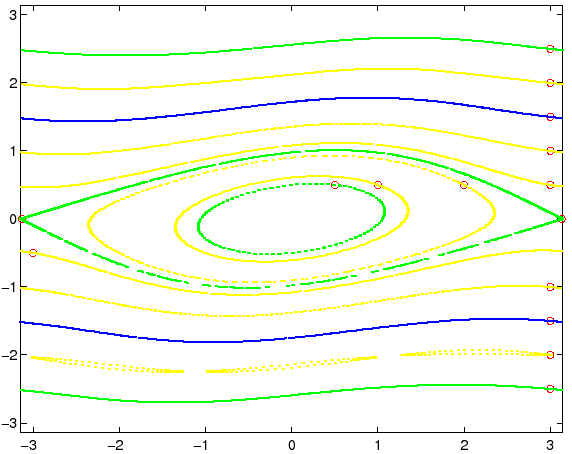
Per osservare che cosa succede per valori intermedi di ![]() , osserviamo le
orbite della mappa standard per i valori
, osserviamo le
orbite della mappa standard per i valori ![]() (Figura 4.4) e
(Figura 4.4) e ![]() (Figura 4.6).
(Figura 4.6).
Per valori relativamente piccoli di ![]() , come nella
Figura 4.4, sembra quasi che il sistema dinamico discreto
ammetta un integrale primo, anche se con le curve di livello distorte
rispetto a quelle della funzione energia del corrispondente sistema
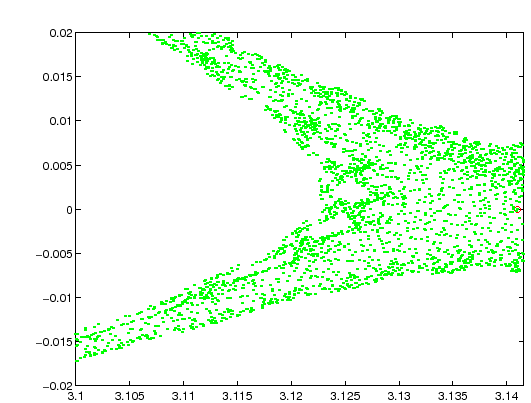
dinamico continuo. Ma se si guarda più in dettaglio, per esempio
ingrandendo la figura, si nota che il comportamento qualitativo delle
orbite del sistema dinamico discreto è molto diverso, ed in
particolare alcune curve invarianti scompaiono: questi fenomeni di
caos si verificano in modo più appariscente
vicino alle separatrici che escono dal punto
di sella (Figura 4.5), ma sono presenti anche vicino
alle separatrici delle isole di risonanza.
, come nella
Figura 4.4, sembra quasi che il sistema dinamico discreto
ammetta un integrale primo, anche se con le curve di livello distorte
rispetto a quelle della funzione energia del corrispondente sistema
dinamico continuo. Ma se si guarda più in dettaglio, per esempio
ingrandendo la figura, si nota che il comportamento qualitativo delle
orbite del sistema dinamico discreto è molto diverso, ed in
particolare alcune curve invarianti scompaiono: questi fenomeni di
caos si verificano in modo più appariscente
vicino alle separatrici che escono dal punto
di sella (Figura 4.5), ma sono presenti anche vicino
alle separatrici delle isole di risonanza.
Per valori più grandi di ![]() , come in Figura 4.6,
l'illusione che la mappa standard possa avere un integrale primo
scompare del tutto. Per questo valore (
, come in Figura 4.6,
l'illusione che la mappa standard possa avere un integrale primo
scompare del tutto. Per questo valore (![]() ) l'ultima curva
invariante corrispondente ad una circolazione è scomparsa, e le
orbite caotiche possono muoversi liberamente lungo tutto l'asse
) l'ultima curva
invariante corrispondente ad una circolazione è scomparsa, e le
orbite caotiche possono muoversi liberamente lungo tutto l'asse
![]() . Si veda la discussione nel Capitolo 6.
. Si veda la discussione nel Capitolo 6.
Problema
Si consideri il problema dei due corpi, cioè il sistema
newtoniano di dimensione 1
Suggerimento: Nel caso continuo, tutte le orbite limitate sono periodiche,
con periodi che dipendono solo dall'integrale dell'energia;
ponendo ![]()
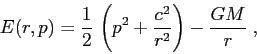
L'impiego di una discretizzazione conservativa può risultare
vantaggioso anche nel caso in cui il sistema dinamico continuo è
dissipativo. Per esempio, applichiamo la mappa standard al sistema
newtoniano dissipativo
Per ottenere un sistema dinamico usiamo, come nel caso della mappa
standard del pendolo,
![]() e otteniamo il sistema
dinamico discreto:
e otteniamo il sistema
dinamico discreto:
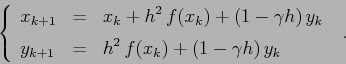
I punti fissi del sistema discreto
soddisfano alle equazioni ![]() (da cui si deduce
(da cui si deduce ![]() ) e
) e
![]() (da cui
(da cui
![]() ); ossia, i punti fissi sono
della forma
); ossia, i punti fissi sono
della forma ![]() con
con ![]() , esattamente i punti di
equilibrio del sistema continuo. Le linearizzazioni in questi punti
fissi hanno matrice
, esattamente i punti di
equilibrio del sistema continuo. Le linearizzazioni in questi punti
fissi hanno matrice
![\begin{displaymath}
A=\left[\begin{array}{cc}{1+h^2\, f'(x_k)}&{1-\gamma h}\\
{h^2\, f'(x_k)}&{1-\gamma h}\end{array}\right]
\end{displaymath}](img1412.png)
Per determinare il carattere delle radici conviene cacolarne il valore
in 0 e 1:
Se invece ![]() , cioè nel caso del minimo dell'energia
potenziale,
, cioè nel caso del minimo dell'energia
potenziale, ![]() e
e ![]() sono entrambe positivi. Se le radici sono
complesse hanno modulo
sono entrambe positivi. Se le radici sono
complesse hanno modulo
![]() . Se invece sono reali non
possono essere maggiori di
. Se invece sono reali non
possono essere maggiori di ![]() perché
perché
![]() e, per
e, per ![]() abbastanza piccolo,
abbastanza piccolo, ![]() . Quindi le
radici, se reali, devono essere entrambe in
. Quindi le
radici, se reali, devono essere entrambe in ![]() , e il punto
fisso è asintoticamente stabile e corrisponde al pozzo del caso continuo. In
altre parole, per
, e il punto
fisso è asintoticamente stabile e corrisponde al pozzo del caso continuo. In
altre parole, per ![]() abbastanza piccolo il sistema discretizzato ha
almeno localmente, nell'intorno dei punti fissi, le stesse proprietà
qualitative del flusso integrale che sta approssimando.
abbastanza piccolo il sistema discretizzato ha
almeno localmente, nell'intorno dei punti fissi, le stesse proprietà
qualitative del flusso integrale che sta approssimando.
Si noti che questa corrispondenza qualitativa è valida solo nell'intorno di un punto di equilibrio iperbolico, cioè nel piano nell'intorno di un pozzo, sella o sorgente. Per punti di equilibrio con esponenti di Lyapounov nulli le proprietà di stabilità non sono necessariamente conservate dalla discretizzazione.
Esercizio
Dato il sistema newtoniano con dissipazione
Andrea Milani 2009-06-01