Next: 6.2 ORBITE PERIODICHE Up: 6. CAOS Previous: 6. CAOS Indice Indice analitico
Sommario La mappa standard è un esempio semplice di sistema dinamico
discreto conservativo che presenta il fenomeno del caos. Facili esperimenti
numerici consentono di percepire la complessità dei comportamenti
dinamici, e anche di trovare una giustificazione per alcuni di questi,
per esempio nel caso del reticolo generato dai punti omoclinici,
intersezioni di una separatrice stabile ed una instabile.
Il concetto di caos è di grande generalità, e si applica a sistemi dinamici sia continui che discreti. Per ottenere una prima presentazione del caos ci occuperemo solo del caso di un sistema dinamico discreto su di uno spazio a due dimensioni. Utilizzeremo a questo scopo un esempio già visto nel Capitolo 4: la mappa standard del pendolo.
La mappa standard è un esempio semplice, nel senso che le equazioni che definiscono la mappa stessa sono una combinazione di poche funzioni elementari, eppure la dinamica da essa definita è, come vedremo, ricca di tutta la complessità caratteristica dei sistemi conservativi caotici.
Richiamiamo la definizione della discretizzazione che trasforma il
pendolo nella mappa standard. Essa contiene il parametro ![]() ,
il passo d'integrazione. Utilizziamo il
sistema di coordinate in cui
,
il passo d'integrazione. Utilizziamo il
sistema di coordinate in cui ![]() contiene
contiene ![]() , cioè svolge la
funzione di incremento su di un passo della coordinata
, cioè svolge la
funzione di incremento su di un passo della coordinata ![]() :
:
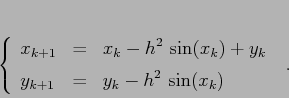
Questa mappa definisce un
sistema dinamico discreto conservativo,
infatti la matrice jacobiana è
![\begin{displaymath}
A(x_k,y_k)= \left[\begin{array}{cc}{1-h^2\,\cos(x_k)}&{1}\\ ...
...&{1}\end{array}\right]
\hspace{5mm},\hspace{5mm}det\, A=+1 \ .
\end{displaymath}](img2091.png)
Questa applicazione, che indichiamo simbolicamente come
![]() , è periodica di periodo
, è periodica di periodo ![]() sia in
sia in ![]() che in
che in
![]() , quindi possiamo anche considerare che
, quindi possiamo anche considerare che ![]() ed
ed ![]() siano
variabili angolo e che la
mappa standard mandi un toro su se stesso.
siano
variabili angolo e che la
mappa standard mandi un toro su se stesso.
La mappa standard (per ogni valore di ![]() ) ha esattamente due
punti fissi, cioè punti
) ha esattamente due
punti fissi, cioè punti ![]() sul toro tali
che
sul toro tali
che ![]() :
: ![]() e
e ![]() . In questi punti la
jacobiana, che definisce il
linearizzato, è
. In questi punti la
jacobiana, che definisce il
linearizzato, è
![\begin{displaymath}
A(X_1)= \left[\begin{array}{cc}{1-h^2}&{1}\\
{-h^2}&{1}\en...
...egin{array}{cc}{1+h^2}&{1}\\
{+h^2}&{1}\end{array}\right]\ .
\end{displaymath}](img2096.png)
Un altro punto con proprietà notevoli è ![]() , tale che
, tale che
![]() e
e
![]() . L'orbita di
. L'orbita di ![]() consiste di due soli punti che si alternano
consiste di due soli punti che si alternano
![]() ; si dice che i due punti
; si dice che i due punti ![]() formano
un'orbita di periodo 2 del sistema dinamico discreto definito da
formano
un'orbita di periodo 2 del sistema dinamico discreto definito da
![]() . La mappa
. La mappa ![]() ha due punti fissi
ha due punti fissi ![]() oltre ai due
posseduti da
oltre ai due
posseduti da ![]() ; il linearizzato si
; il linearizzato si ![]() in
in ![]() è dato dalla matrice
è dato dalla matrice
![\begin{displaymath}
A^{(2)}= A(X_4)\, A(X_3)= \left[\begin{array}{cc}{1+h^2}&{1}...
...}{cc}{1-h^2-h^4}&{2+h^2}\\
{-h^4}&{1+h^2}\end{array}\right]
\end{displaymath}](img2105.png)
Si noti che non si può decidere sulla base della sola
linearizzazione se ![]() è una mappa stabile
nel punto
è una mappa stabile
nel punto ![]() ; lo stesso per
; lo stesso per ![]() in
in ![]() ed
ed ![]() . In effetti in
questi punti è stabile, ma per dimostrarlo occorre usare un teorema
difficile (vedi alla Sezione 6.4). Invece nella sella
nonlineare
. In effetti in
questi punti è stabile, ma per dimostrarlo occorre usare un teorema
difficile (vedi alla Sezione 6.4). Invece nella sella
nonlineare ![]() è una mappa instabile per la
presenza di una separatrice instabile
(vedi più avanti in questa Sezione).
è una mappa instabile per la
presenza di una separatrice instabile
(vedi più avanti in questa Sezione).
 |
Poiché l'orbita di un punto ![]() si può calcolare direttamente
iterando la mappa:
si può calcolare direttamente
iterando la mappa: ![]() , e questo richiede un numero molto
ridotto di calcoli (precisamente il calcolo di un seno e tre
operazioni aritmetiche) per iterazione, è molto facile eseguire
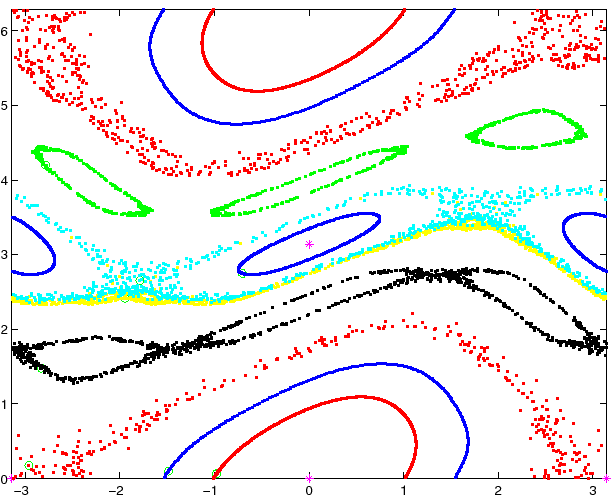
``esperimenti al calcolatore'' sulla mappa standard. Nella
Figura 6.1 sono indicati con circoletti le condizioni
iniziali, ciascuna con la sua orbita (per
, e questo richiede un numero molto
ridotto di calcoli (precisamente il calcolo di un seno e tre
operazioni aritmetiche) per iterazione, è molto facile eseguire
``esperimenti al calcolatore'' sulla mappa standard. Nella
Figura 6.1 sono indicati con circoletti le condizioni
iniziali, ciascuna con la sua orbita (per ![]() ) calcolata per 1000
iterazioni.
) calcolata per 1000
iterazioni.
Un programma Matlab per eseguire esperimenti sulla mappa standard: stmapauto.m
Nella figura sono evidenti due tipi molto diversi di comportamento
dinamico. Alcune orbite, per esempio con condizioni iniziali vicine al
punto fisso iperbolico ![]() , sembrano riempire una
regione caotica. Altre invece, per esempio con condizioni
iniziali abbastanza vicine al punto fisso ellittico
, sembrano riempire una
regione caotica. Altre invece, per esempio con condizioni
iniziali abbastanza vicine al punto fisso ellittico ![]() , oppure
con condizioni iniziali molto vicine al punto periodico ellittico
, oppure
con condizioni iniziali molto vicine al punto periodico ellittico
![]() , sembrano disporsi su una curva invariante di Moser,
con una o più componenti connesse, e appartengono a una
regione ordinata. Si intuisce la presenza di qualche altro
punto periodico, cioè punti
, sembrano disporsi su una curva invariante di Moser,
con una o più componenti connesse, e appartengono a una
regione ordinata. Si intuisce la presenza di qualche altro
punto periodico, cioè punti ![]() tali che
tali che ![]() per un qualche periodo intero
per un qualche periodo intero ![]() ; per
esempio al centro dei gruppi di tre ``isole'' ci dovrebbe essere un
punto di periodo tre.
; per
esempio al centro dei gruppi di tre ``isole'' ci dovrebbe essere un
punto di periodo tre.
Per quale ragione si possono verificare comportamenti così diversi? Quali sono le proprietà rigorose delle orbite nelle regioni ordinate: esistono veramente delle curve invarianti? E quali sono le proprietà rigorose delle regioni caotiche: si tratta di insiemi aperti in cui una singola orbita è densa? Si può in qualche modo caratterizzare l'insieme delle orbite periodiche? Questo capitolo è dedicato ad una risposta molto parziale a queste domande.
Nella Figura 6.1 è chiaro che la regione caotica
contiene il punto fisso iperbolico ![]() . Perciò occorre per
prima cosa studiare il comportamento della mappa standard, e delle sue
iterate, in un intorno di questo punto.
. Perciò occorre per
prima cosa studiare il comportamento della mappa standard, e delle sue
iterate, in un intorno di questo punto.
Il teorema che segue si applica non solo alla mappa standard ma a
qualsiasi diffeomorfismo ![]() di
di ![]() in se stesso, oppure di
in se stesso, oppure di ![]() in se stesso; ossia
in se stesso; ossia
![]() dove
dove ![]() possono essere sia
numeri reali che variabili angolo.
possono essere sia
numeri reali che variabili angolo.
Sia ![]() un punto fisso iperbolico per
un punto fisso iperbolico per ![]() , sia
, sia ![]() la matrice del
linearizzato in
la matrice del
linearizzato in ![]() .
.
(a) Esiste una curva regolare iniettiva
![]() (oppure
(oppure
![]() ) tale che
) tale che
(b) Esiste una curva regolare iniettiva
![]() (oppure
(oppure
![]() ) tale che
) tale che
Questa curva si chiama separatrice instabile.
Dimostrazione (facoltativa):
Viene data soltanto una traccia di dimostrazione; per una
dimostrazione completa, si veda per esempio [Hartmann 64].
Mediante un cambiamento di coordinate locale, nell'intorno di ![]() ,
riconduciamoci al caso in cui
,
riconduciamoci al caso in cui ![]() , l'asse
, l'asse ![]() è
l'autospazio di
è
l'autospazio di ![]() e l'asse
e l'asse ![]() è l'autospazio di
è l'autospazio di
![]() ; cioè
; cioè
![]() . In questo sistema
di coordinate la mappa
. In questo sistema
di coordinate la mappa
![]() è della forma
è della forma
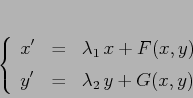
Per completare la dimostrazione, occorre far vedere che la funzione
invariante ![]() è differenziabile (mostrando che la convergenza
ha luogo anche nello spazio completo delle funzioni
è differenziabile (mostrando che la convergenza
ha luogo anche nello spazio completo delle funzioni ![]() ). Inoltre,
scelto un punto
). Inoltre,
scelto un punto ![]() sulla curva invariante, la sua
immagine appartiene ancora alla curva e quindi è della forma
sulla curva invariante, la sua
immagine appartiene ancora alla curva e quindi è della forma
![]() ; si noti che per
; si noti che per ![]() abbastanza piccolo
abbastanza piccolo
![]() perche'
perche' ![]() . Dato il segmento di curva
. Dato il segmento di curva
![]() definito sul segmento
definito sul segmento
![]() si può
prolungare la definizione della curva invariante ad un intervallo
arbitrariamente largo imponendo la condizione 3., cioè ponendo per
definizione per ogni
si può
prolungare la definizione della curva invariante ad un intervallo
arbitrariamente largo imponendo la condizione 3., cioè ponendo per
definizione per ogni ![]()
La dimostrazione relativa all'altra separatrice, che ha la forma ![]() ,
è analoga.
,
è analoga.
C.D.D.
Esempio:
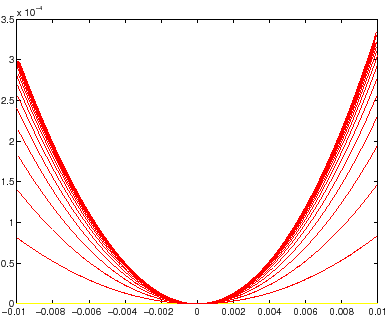 |
La presenza, nell'intorno di un punto fisso iperbolico, di due
separatrici non spiega di per sé la formazione del caos. Una
relazione però esiste se si suppone che le due curve invarianti
non terminino in un punto fisso (come accade per le separatrici del
pendolo nel caso continuo). Ne segue che non possono terminare
affatto, cioè non può esistere né
![]() né
né
![]() (e neppure i limiti
per
(e neppure i limiti
per ![]() ): tali punti sarebbero insiemi
limite e quindi punti fissi (per l'equivalente
discreto del teorema del punto limite). Se la mappa
): tali punti sarebbero insiemi
limite e quindi punti fissi (per l'equivalente
discreto del teorema del punto limite). Se la mappa ![]() è definita su
è definita su ![]() , che è compatto, in generale l'immagine
, che è compatto, in generale l'immagine
![]() non sarà un chiuso perché possiede dei valori limite
che non gli appartengono (lo stesso per
non sarà un chiuso perché possiede dei valori limite
che non gli appartengono (lo stesso per
![]() ), ma deve
``avvolgersi'' infinite volte attorno a questi punti limite.
), ma deve
``avvolgersi'' infinite volte attorno a questi punti limite.
Per chiarire questo comportamento ``all'infinito'' delle separatrici
utilizziamo un esperimento numerico, che costruisce esplicitamente,
mediante iterazioni della mappa standard, un tratto necessariamente
finito ma molto lungo delle due separatrici. (Attenzione: il
ragionamento che segue vale per ![]() , come è vero per il
punto iperbolico
, come è vero per il
punto iperbolico ![]() della mappa standard del pendolo;
altrimenti bisognerebbe ricondursi a questo caso usando la mappa
della mappa standard del pendolo;
altrimenti bisognerebbe ricondursi a questo caso usando la mappa
![]() .)
.)
Il procedimento consiste nel costruire un'approssimazione di un
segmento di una separatrice: per esempio se ![]() è un punto fisso
iperbolico e
è un punto fisso
iperbolico e ![]() è un autovettore del suo linearizzato
è un autovettore del suo linearizzato ![]() con
autovalore
con
autovalore ![]() , si scelga un numero
, si scelga un numero ![]() piccolo e si
prenda il punto
piccolo e si
prenda il punto
![]() che non appartiene alla
separatrice instabile, ma ha una distanza da essa di ordine superiore
rispetto ad
che non appartiene alla
separatrice instabile, ma ha una distanza da essa di ordine superiore
rispetto ad ![]() per
per ![]() (perchè la separatrice
è tangente all'autospazio in
(perchè la separatrice
è tangente all'autospazio in ![]() ).
).
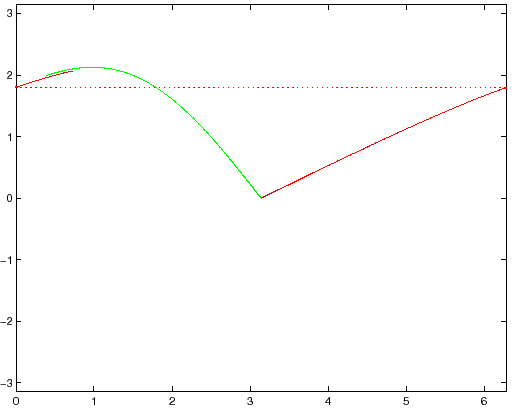 |
La sua immagine ![]() sarà pure vicina alla separatrice
stabile, essendo della forma
sarà pure vicina alla separatrice
stabile, essendo della forma
![]() . Il segmento
. Il segmento ![]() che congiunge questi due punti è
un'approssimazione di un segmento della separatrice.
Tracciamo l'immagine
che congiunge questi due punti è
un'approssimazione di un segmento della separatrice.
Tracciamo l'immagine ![]() , che sta più lontana dal punto fisso:
essa ancora non appartiene alla separatrice, ma è più vicina ad
essa di quanto non lo fosse
, che sta più lontana dal punto fisso:
essa ancora non appartiene alla separatrice, ma è più vicina ad
essa di quanto non lo fosse ![]() , perchè l'effetto della mappa
, perchè l'effetto della mappa ![]() è una contrazione (di un fattore
è una contrazione (di un fattore ![]() ) nella direzione
) nella direzione
![]() trasversa a
trasversa a ![]() . Dopo un certo numero di iterazioni, la
distanza tra
. Dopo un certo numero di iterazioni, la
distanza tra ![]() e la separatrice instabile è diventata del
tutto trascurabile. Tracciamo in un grafico tutti i punti di
e la separatrice instabile è diventata del
tutto trascurabile. Tracciamo in un grafico tutti i punti di
![]() per un
per un ![]() elevato, e questi rappresenteranno,
con un'approssimazione molto buona, un segmento ``abbastanza lungo''
della separatrice instabile.
elevato, e questi rappresenteranno,
con un'approssimazione molto buona, un segmento ``abbastanza lungo''
della separatrice instabile.
Si può procedere in modo analogo per la separatrice stabile:
cominciando con il segmento ![]() di estremi
di estremi
![]() (dove
(dove ![]() è un autovettore di autovalore
è un autovettore di autovalore ![]() ) e
) e
![]() , che è vicino alla separatrice, si iteri
la mappa inversa
, che è vicino alla separatrice, si iteri
la mappa inversa ![]() avvicinandosi alla
separatrice. Tracciamo
avvicinandosi alla
separatrice. Tracciamo
![]() come
approssimazione di un segmento ``abbastanza lungo'' della separatrice
stabile.
come
approssimazione di un segmento ``abbastanza lungo'' della separatrice
stabile.
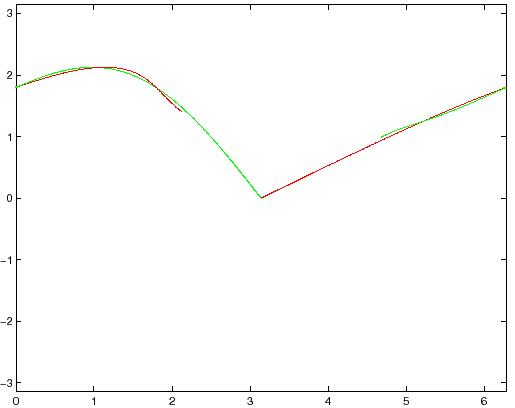 |
Le Figure 6.3-6.5 mostrano il
risultato della costruzione precedente, con
![]() . Le
separatrici restano vicine ai corrispondenti autospazi finchè la
distanza dal punto fisso è piccola, poi hanno un comportamento
nonlineare. Quando raggiungono il bordo del quadrato
ricompaiono sul lato opposto, che si deve considerare identificato. A
un certo punto la separatrice stabile e la separatrice instabile si
incrociano. Per il teorema qui sopra ciascuna delle due
separatrici è una curva iniettiva, quindi una
separatrice non può incrociare se stessa, ma niente impedisce che
incroci l'altra.
. Le
separatrici restano vicine ai corrispondenti autospazi finchè la
distanza dal punto fisso è piccola, poi hanno un comportamento
nonlineare. Quando raggiungono il bordo del quadrato
ricompaiono sul lato opposto, che si deve considerare identificato. A
un certo punto la separatrice stabile e la separatrice instabile si
incrociano. Per il teorema qui sopra ciascuna delle due
separatrici è una curva iniettiva, quindi una
separatrice non può incrociare se stessa, ma niente impedisce che
incroci l'altra.
Un programma Matlab per tracciare le separatrici del punto fisso iperbolico della mappa standard: stmasep.m
 |
Definizione:
Sia ![]() un punto fisso iperbolico di un diffeomorfismo
un punto fisso iperbolico di un diffeomorfismo
![]() (oppure
(oppure
![]() ), e siano
), e siano ![]() l'insieme di punti della sua separatrice stabile,
l'insieme di punti della sua separatrice stabile, ![]() quello della sua separatrice instabile.
Un punto
quello della sua separatrice instabile.
Un punto
![]() si dice punto omoclinico.
si dice punto omoclinico.
Un punto si dice doppiamente asintotico se la sua orbita ha come
limite una sola orbita sia per ![]() che per
che per ![]() .
Un punto omoclinico è doppiamente asintotico, con in più la
proprietà che ``tende allo stesso'' punto
.
Un punto omoclinico è doppiamente asintotico, con in più la
proprietà che ``tende allo stesso'' punto ![]() , dai due lati: cioè
, dai due lati: cioè
![]() (perchè
(perchè ![]() ) e anche
) e anche
![]() (perchè
(perchè ![]() ).
).
Per il punto omoclinico passano le due separatrici, intese come curve
parametrizzate
![]() ; poichè sono curve
regolari, hanno un vettore velocità (derivata rispetto al parametro
; poichè sono curve
regolari, hanno un vettore velocità (derivata rispetto al parametro
![]() ) non nullo:
) non nullo: ![]() e
e ![]() .
. ![]() si dice
punto omoclinico trasversale se
si dice
punto omoclinico trasversale se ![]() e
e ![]() sono linearmente indipendenti. In questo caso si può stabilire se la
separatrice stabile viene da destra o da sinistra rispetto alla
separatrice instabile, a seconda del segno del seno dell'angolo tra i
due vettori velocità.
sono linearmente indipendenti. In questo caso si può stabilire se la
separatrice stabile viene da destra o da sinistra rispetto alla
separatrice instabile, a seconda del segno del seno dell'angolo tra i
due vettori velocità.
Proprietà:
(a) Se ![]() è un punto omoclinico, allora tutti i punti
è un punto omoclinico, allora tutti i punti
![]() della sua orbita sono omoclinici. Si parla in questo caso di
orbita omoclinica.
della sua orbita sono omoclinici. Si parla in questo caso di
orbita omoclinica.
(b) Se ![]() è un punto omoclinico trasversale, allora tutti i punti della
sua orbita hanno la stessa proprietà.
è un punto omoclinico trasversale, allora tutti i punti della
sua orbita hanno la stessa proprietà.
(c) Sia ![]() una mappa conservativa, cioè con jacobiano
una mappa conservativa, cioè con jacobiano ![]() in ogni
punto. Allora, se
in ogni
punto. Allora, se ![]() è un punto omoclinico trasversale e in
è un punto omoclinico trasversale e in ![]() la
separatrice stabile viene da destra rispetto alla separatrice
instabile, lo stesso succede in tutti i punti dell'orbita di
la
separatrice stabile viene da destra rispetto alla separatrice
instabile, lo stesso succede in tutti i punti dell'orbita di ![]() .
.
(a) Poichè ![]() e
e ![]() sono insiemi invarianti per
sono insiemi invarianti per ![]() ,
così è la loro intersezione.
,
così è la loro intersezione.
(b) ![]() è un diffeomorfismo, quindi il suo differenziale è
invertibile; se due vettori velocità sono linearmente indipendenti,
le loro immagini restano indipendenti.
è un diffeomorfismo, quindi il suo differenziale è
invertibile; se due vettori velocità sono linearmente indipendenti,
le loro immagini restano indipendenti.
(c) Se lo jacobiano è positivo, il diffeomorfismo ![]() conserva l'orientazione.
conserva l'orientazione.
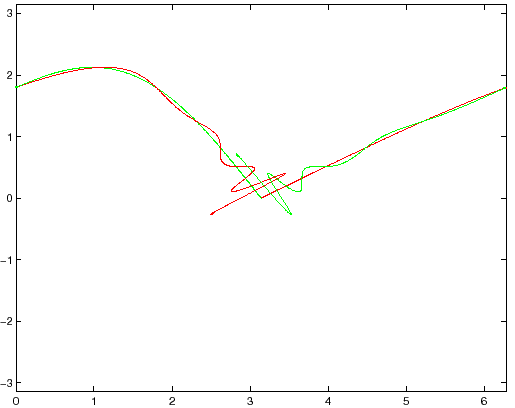
Da queste proprietà segue che se continuiamo le iterazioni nella procedura numerica delle Figure 6.3-6.5 ci saranno per forza altre intersezioni, in numero sempre crescente (Figura 6.6). Le orbite omocliniche sono almeno due, perchè ci sono due incroci tra le separatrici con orientazione differente.
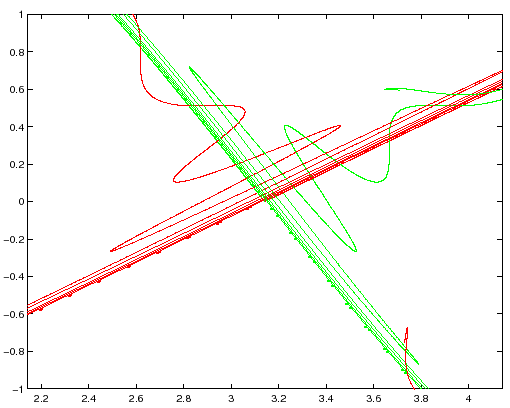 |
Che cosa succede se si va avanti con l'esperimento? Non posso trovare
parole migliori, per anticipare quello che si può vedere nello
stesso grafico per ![]() più grande, di quelle usate da chi ha
inventato questo esperimento, pur non avendo un calcolatore per farlo:
Henri Poincaré scriveva [Poincaré 1899] (mia traduzione dal francese):
più grande, di quelle usate da chi ha
inventato questo esperimento, pur non avendo un calcolatore per farlo:
Henri Poincaré scriveva [Poincaré 1899] (mia traduzione dal francese):
Che si cerchi di raffigurarsi la figura formata da queste due curve e dalle loro intersezioni in numero infinito, ciascuna delle quali corrisponde ad una soluzione doppiamente asintotica, queste intersezioni formeranno una specie di reticolo, di tessuto, di rete a maglie infinitamente strette; ciascuna delle due curve non deve mai intersecarsi da sola, ma deve ripiegarsi su se stessa in un modo molto complicato per venire a tagliare un numero infinito di volte tutte le maglie della rete.
Si sarà colpiti dalla complessità di questa figura, che io non cerco neppure di disegnare. Non c'è niente di più appropriato a darci un'idea della complicazione del problema dei tre corpi, e in generale di tutti i problemi della Dinamica non integrabili... [Pagina 389]
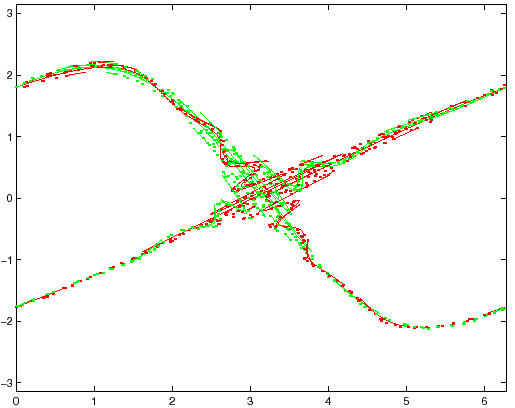 |
Dunque, Poincaré ha scoperto il caos (anche se non usava questo nome, che è stato introdotto nel 1970). Il problema modello di cui si era servito era quello dei tre corpi della meccanica celeste, il che comporta delle difficoltà tecniche che abbiamo evitato in questo testo ricorrendo ad un esempio più semplice. Questo si può fare perché il fenomeno del caos è universale nei problemi di dinamica conservativi non integrabili, dei quali i più semplici sono le mappe conservative a due dimensioni.
Procedendo con l'esperimento, vediamo apparirci sullo schermo del calcolatore proprio la figura che Poincaré non osava disegnare, ma che era riuscito a immaginarsi senza l'ausilio di quel calcolatore, di cui oggi è difficile pensare di fare a meno. Le Figure 6.5-6.7 mostrano come le separatrici si intrecciano, e formano una regione che non abbiamo difficoltà a qualificare caotica, anche se ci manca ancora sia una definizione rigorosa di caos, sia un procedimento descrittivo che vada al di là delle parole di ammirazione di Poincaré per la complessità della dinamica.
Andrea Milani 2009-06-01