A.3 TOPOLOGIA

Norme

Definizione:

Una norma sullo spazio ${\bf R}^n$ è una funzione $N:{\bf R}^n \longrightarrow {\bf R}$ che soddisfa, per ogni $X,Y\in {\bf R}^n$ e $c\in{\bf R}$, alle tre proprietà seguenti:


$$N(X)\geq 0 \ e\ N(X)=0 \Leftrightarrow X=\underline 0$$ (A.1)

$$N(X+Y)\leq N(X)+N(Y)$$ (A.2)

$$N(cX)=\vert c\vert\,N(X)$$ (A.3)

Esempio:

La norma euclidea si indica con lo stesso simbolo del modulo:


$$X=(x_i)\in {\bf R}^n \Longrightarrow \vert X\vert=\sqrt{\sum_{k=1}^n x_k^2}$$


ed è legata al prodotto scalare: $\vert X\vert^2= X\cdot X$. Per verificare la diseguaglianza triangolare $\vert X+Y\vert\leq \vert X\vert+\vert Y\vert$ si usa la diseguaglianza di Cauchy:

$$-\vert X\vert\, \vert Y\vert\leq X\cdot Y \leq \vert X\vert\, \vert Y\vert\ .$$

Esempio:

Consideriamo lo spazio vettoriale ${\bf R}^{n\times n}$ delle matrici quadrate $n\times n$. Ogni matrice $A$ si può anche considerare come un operatore lineare su ${\bf R}^n$. Allora possiamo associare ad $A$ la norma uniforme dell'operatore lineare:

$$\vert\vert A\vert\vert= \max_{\vert X\vert=1} \vert AX\vert .$$



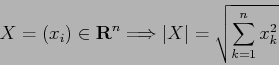
Il massimo esiste perché la sfera $\vert X\vert=1$ di ${\bf R}^n$ è un compatto. Oltre alle tre proprietà che fanno parte della definizione di norma (e che dovrebbero essere verificate), la norma uniforme soddisfa anche alle seguenti:


$$\vert AX\vert \leq \vert\vert A\vert\vert\, \vert X\vert$$ (A.4)

$$\vert\vert A\,B\vert\vert \leq \vert\vert A\vert\vert\,\vert\vert B\vert\vert$$ (A.5)

$$\vert\vert A^n\vert\vert \leq\vert\vert A\vert\vert^n .$$ (A.6)




Si potrebbe definire la norma uniforme anche a partire da un'altra norma di ${\bf R}^n$ diversa da quella euclidea, usando le stesse formule con $N(X)$ al posto di $\vert X\vert$; tutte le sei proprietà citate sopra sarebbero comunque valide.

Esempio:

La norma del massimo è definita dal massimo modulo delle componenti:


$$X=(x_i)\in {\bf R}^n \Longrightarrow \vert X\vert _0=max_{j=1,n} \vert x_j\vert$$

Definizione:

Uno spazio metrico è un insieme dotato di una distanza, cioè una funzione $d(X,Y)$ definita per $X,Y\in S$ con le proprietà


$$d(X,Y)\geq 0\hspace{5mm},\hspace{5mm}d(X,Y)=0 \Longleftrightarrow X=Y$$ (A.7)

$$d(X,Y)=d(Y,X)$$ (A.8)

$$d(X,Y)+d(Y,Z)\leq d(X,Z)$$ (A.9)

Ogni spazio vettoriale dotato di una norma è uno spazio metrico: basta porre $d(X,Y)=\vert\vert X-Y\vert\vert$.

Topologia in ${\bf R}^n$

Le nozioni di topologia utilizzate in questo corso si riferiscono soltanto agli insiemi ${\bf R}^n$ ed ai loro sottoinsiemi. In questo ambito, basta sapere che le palle di raggio $\delta$

$$B_\delta = \{ X \vert\; \vert X-X_S\vert<\delta\}$$

formano un sistema fondamentale di intorni del punto $X_S\in {\bf R}^n$ che definisce la topologia, cioè gli insiemi aperti di ${\bf R}^n$, che sono tutte e sole le unioni degli intorni di tutti i punti.

Se $\vert\vert X\vert\vert=\vert X\vert$ è la norma euclidea, e $\vert\vert X\vert\vert _V$ è un'altra norma per i vettori $X\in {\bf R}^n$, allora esistono due costanti positive $\alpha$ e $\beta$ tali che

$$\alpha \vert\vert X\vert\vert \leq \vert\vert X\vert\vert _V \leq \beta \vert\vert X\vert\vert$$

Quindi le palle $\vert\vert X-X_S\vert\vert _V<\delta$ usate come sistema fondamentale di intorni definiscono la stessa topologia, cioè gli stessi aperti definiti dagli intorni $B_\delta$. Le nozioni di limite e di continuità di una funzione dipendono solo dalla topologia, quindi sono indipendenti dalla scelta di una norma negli spazi ${\bf R}^n$.

Il complementare di un aperto è un chiuso; un insieme $C$ tale che ogni successione di suoi punti, e che ammette limite, ha limite pure appartenente a $C$, è un chiuso.

Data una successione $X_n, \; n\in {\bf N}$, se esiste una sottosuccesione $X_{n_k}$ convergente ad un punto $X^*$ si dice che $X^*$ è un valore limite; sostanzialmente la stessa definizione vale anche per una funzione $X(t), \; t\in {\bf R}$: se esiste una successione $t_n$ di valori della variabile indipendente tale che $\lim_{n\to +\infty}\;t_n=t^*$ e $\lim_{n\to+\infty}\; X(t_n)= X^*$ si dice che $X^*$ è un valore limite per $t\to t^*$.

Un insieme $K$ tale che ogni successione di suoi punti ammette un valore limite pure appartenente a $K$ (cioè ha una sottosuccessione convergente ad un punto di $K$) è un compatto; esiste un'altra definizione di compatto (basata sui ricoprimenti), ma nel contesto che ci interessa le due definizioni sono equivalenti. Un insieme è compatto se e solo se è limitato e chiuso.

Una funzione continua su di un insieme compatto ha massimo e minimo.

Un omeomorfismo è un'applicazione biunivoca, continua, e con inversa continua; due insiemi omeomorfi hanno in comune tutte le proprietà che dipendono solo dalla topologia (ma non necessariamente proprietà metriche, come il volume).

La frontiera di un insieme $C$ è l'insieme dei i punti tali che tutti i loro intorni contengono sia punti di $C$ che punti non in $C$. Un chiuso contiene tutti i suoi punti di frontiera, un aperto non ne contiene nessuno. La parte interna di un insieme è l'insieme meno la frontiera, o il più grande aperto contenuto nell'insieme stesso.

Benché il punto all'infinito non appartenga ad ${\bf R}^n$, è sempre legittimo parlare di limite infinito di una successione o funzione a valori in ${\bf R}^n$, pur di considerare che gli insiemi

$$K_\delta = \{ X \vert\; \vert X-X_S\vert>\delta\}$$

siano un sistema fondamentale di intorni del punto all'infinito.

Un insieme $C$ è connesso se non si può scomporre in due insiemi non vuoti $C_1=C\cap A$ e $C_2=C\cap B$ con $C_1\cap C_2$ vuoto, $A,B$ aperti. Se al contrario una tale scomposizione è possibile, i più grandi insiemi connessi contenuti in $C$ si dicono le sue componenti connesse. Se $C$ è l'immagine di una curva continua, semplice e chiusa, in ${\bf R}^2$, allora il complementare di $C$ in ${\bf R}^2$ ha esattamente due componenti connesse, una (l'interno) limitata, una (l'esterno) illimitata, tali che $C$ fa da frontiera ad entrambe.

Bibliografia :

-

Prodi, G. : Analisi matematica, Bollati Boringhieri, 1970.

-

Checcucci, V., Tognoli, A. e Vesentini, E.: Lezioni di topologia generale, Feltrinelli 1967.

-

Hall, D. W. e Spencer, G. L. : Elementary topology, John Wiley and Sons, 1955.