A.2 CALCOLO IN PIÙ VARIABILI

Calcolo differenziale in più variabili

Una funzione $f : {\bf R}^m \to {\bf R}^n$ è differenziabile se è approssimabile nell'intorno di ogni punto con una funzione lineare, con resto di ordine di infinitesimo superiore al primo nella distanza dal punto. Il differenziale è l'applicazione lineare approssimante, che è espressa (nelle basi canoniche degli spazi di partenza e di arrivo) da una matrice $n\times m$ detta matrice jacobiana. Per le funzioni scalari, cioè a valori in ${\bf R}$, la matrice è di tipo $1\times m$, cioè un vettore riga, il gradiente. Una funzione $C^1$ è sempre differenziabile. La composta di due funzioni differenziabili è differenziabile, e la sua matrice jacobiana, associata all'applicazione lineare composta, è il prodotto righe per colonne delle due matrici jacobiane (con la jacobiana della seconda funzione a sinistra).

Se $f(x_1,x_2,\ldots\,x_n)$ è una funzione definita e di classe $C^2$ (su di un aperto $W\subset{\bf R}^n$), allora le derivate seconde miste sono uguali:

$$\frac{\partial^2 {f}}{\partial {x_i}\,\partial{x_k}} = \frac... ...x_k}\,\partial{x_i}}\hspace{5mm},\hspace{5mm} i,k =1,\ldots, n$$

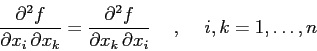
Quindi la matrice hessiana delle derivate seconde è simmetrica.

Un punto di minimo locale forte è dove una funzione assume un valore strettamente minore di tutti i valori assunti in un intorno. Se una funzione è di classe $C^2$, ha un punto stazionario (dove ha gradiente nullo) e matrice hessiana definita positiva, si parla di punto di minimo locale non degenere; tale punto è anche di minimo locale forte.

Sia $f\,:\, W \longrightarrow \, {\bf R}$, di classe $C^s$ (con $s\geq 1$) sull'aperto $W$ di $R^2$, e $X_0$ un punto di $W$ con $f(X_0)=c$. Se il gradiente di $f$ è non nullo in $X_0$, allora esiste una funzione di classe $C^s$ $g\,:\, U \, \longrightarrow \, W$, con $U$ un intorno di $0$ in ${\bf R}$ tale che

$$\left\{\begin{array}{lcl} {\displaystyle g(0)} & {\display... ...} & {\displaystyle=} &{\displaystyle c} \end{array}\right.\;.$$

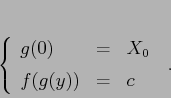
Questa funzione è localmente unica, cioè non ci sono in un intorno di $X_0$ altri punti soddisfacenti a $f(X)=c$ salvo le immagini di $g$.

Le curve di livello della funzione $f$ sono regolari; inoltre la loro velocità è ortogonale al gradiente di $f$.

Sia $F\,:\, W \longrightarrow \, {\bf R}^n$, di classe $C^s$ (con $s\geq 1$) sull'aperto $W$ di $R^n$, con $n>k$, e $X_0$ un punto di $W$ con $F(X_0)=C$. Se la matrice jacobiana di $F$ è invertibile (cioè se lo jacobiano è $\neq 0$), allora esiste una funzione $G\,:\, U \, \longrightarrow \, V$ con $U$ un intorno di $C$, e $V$ un intorno di $X_0$, di classe $C^s$, che è l'inversa di $F$ ristretta a $V$: $F(G(Y))=Y\;,\; G(F(X))=X$.

Le due applicazioni $F,G$ si dicono diffeomorfismi locali.

Un corollario del teorema della funzione inversa è che un punto di minimo locale non degenere è isolato tra i punti di minimo locale della funzione.

Calcolo integrale in più variabili

Richiamiamo la teoria della integrazione di Riemann, nella quale gli integrali sono definiti usando il limite per ampiezza della partizione che tende a zero. Un insieme sul quale si può integrare la funzione 1, ottenendone l'area, si dice misurabile secondo Peano-Jordan.

Una funzione continua su di un insieme misurabile secondo Peano-Jordan ammette sempre l'integrale di Riemann.

Con procedimenti del tutto simili si può definire l'integrale definito in una variabile, l'integrale doppio di una qualsiasi funzione limitata e continua su di un insieme misurabile.

Dato un insieme misurabile (secondo Peano-Jordan) $D\subset {\bf R}^2$, ed un diffeomorfismo

$$\Phi\;:\; D'\; \longrightarrow D\hspace{5mm},\hspace{5mm}\Phi\;:\; (u,v)\;\longmapsto \; (x,y)$$

allora l'integrale doppio di una funzione continua $f(x,y)$ su $D$ si può calcolare mediante un integrale nelle variabili $(u,v)$:

$$\int_D\;f(x,y)\,\,dx\,dy = \int_{D'}\; f(x(u,v),y(u,v))\,\l... ...rac{\partial {(x,y)}}{\partial {(u,v)}}\right\vert \, \,du\,dv$$

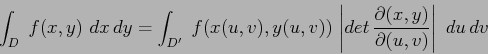
Per esempio, se la funzione da integrare è identicamente uguale ad 1, si trova che un diffeomorfismo conserva l'area se e solo se il determinante jacobiano vale $\pm 1$ in ogni punto. Però se il determinante è $-1$, il diffeomorfismo non conserva l'orientazione, ossia manda angoli positivi (antiorari) in angoli negativi (orari). Perciò in molte applicazioni, come nel caso dei sistemi conservativi, si richiede che l'area venga conservata ``con il segno'', cioè con determinante jacobiano identicamente uguale ad 1.

Integrali di linea, forme differenziali nel piano

Una curva regolare è una parametrizzazione, cioè una funzione $s\longmapsto X(s)$ definita su di un intervallo di ${\bf R}$ ed a valori in ${\bf R}^n$, che sia differenziabile (di classe almeno $C^1$) e la cui velocità $dX/ds(s)$ non si annulli per nessun $s$. Le soluzioni di sistemi dinamici continui sono sempre curve regolari, con il tempo come parametro, salvo che nel caso dei punti di equilibrio (le uniche soluzioni per cui la velocità si annulla).

Un integrale di linea di una forma differenziale lineare nel piano $(x,y)$ viene indicato come

$$\int_C \; [P(x,y)\,dx + Q(x,y)\, dy]$$

dove $C$ è una curva regolare; se $C\;:\; t \; \longmapsto (x(t),y(t))$ è la parametrizzazione della curva con due funzioni $C^1$, con $t\in [a,b]$, allora l'integrale di linea è per definizione uguale all'integrale definito:

$$\int_C \, [P(x,y)\,dx + Q(x,y)\, dy]= \int_a^b\,\left[P(x(t... ...{t}} (t) + Q(x(t),y(t))\,\frac{d{y}}{d{t}} (t)\right]\, dt\;.$$

La forma differenziale lineare è l'espressione $P\,dx+ Q\,dy$; il vettore dei suoi coefficienti è covariante. Poiché il vettore velocità $(dx/dt, dy/dt)$ è invece controvariante, cioè si trasforma con l'inverso della jacobiana, se si cambia sistema di coordinate l'integrale di linea non cambia.

Un insieme $D$ del piano ${\bf R}^2$ ha bordo $C=\partial D$ se $C$ è la frontiera di $D$, e al tempo stesso è l'immagine di una curva regolare. Inoltre si richiede che la parametrizzazione sia tale che la curva si lascia $D$ a sinistra del vettore velocità. Nella teoria dell'integrazione si può anche considerare una curva regolare a tratti, per cui per esempio si può integrare sul bordo di un poligono (con lati rettilinei, o curvilinei).

La formula di Green per l'area fornisce una relazione tra l'integrale doppio che definisce l'area di un insieme piano $D$, ed un integrale di linea sulla curva che ne forma il bordo $C=\partial D$:

$$Area(D)=\int\!\!\!\int _D\;1\;\,dx\,dy = -\int_C\; y\,dx = -\int_C x\,dy\;.$$

Una forma chiusa si ha quando le funzioni $P(x,y)$ e $Q(x,y)$ sono $C^1$ ed il rotore

$$\frac{\partial {Q}}{\partial {x}} - \frac{\partial {P}}{\partial {y}}$$

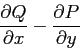
è identicamente nullo (su di un aperto $W\subset {\bf R}^2$). Una forma differenziale lineare su di un aperto $W\subset {\bf R}^2$ è una forma esatta quando $P\,dx + Q\, dy=d\,F(x,y)$, ossia quando le due funzioni $P(x,y)\,,\, Q(x,y)$ definiscono un campo vettoriale conservativo che coincide con il gradiente di una funzione differenziabile $F$:

$$\frac{\partial {F}}{\partial {x}}=P(x,y) \hspace{5mm},\hspace{5mm}\frac{\partial {F}}{\partial {y}}=Q(x,y)\;.$$

Una forma differenziale chiusa su di un aperto $W\subset {\bf R}^2$ (cioè un campo vettoriale con rotore identicamente nullo su tutto $W$) è sempre localmente esatta, su di un intorno di ogni punto di $W$; viceversa una forma localmente esatta (con coefficienti di classe almeno $C^1$) è anche chiusa, per il teorema delle derivate miste. Poiché il gradiente di una funzione, e la forma differenziale lineare corrispondente, si trasformano nello stesso modo covariante, la proprietà di essere localmente esatta (quindi chiusa) non dipende dal sistema di coordinate impiegato.

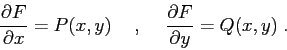
Non è invece detto che una forma chiusa sia esatta; in generale sarà la forma $d\,F$ associata ad una funzione polidroma $F$. Se però l'insieme $W$ soddisfa ad opportune condizioni topologiche, come quella di essere semplicemente connesso, allora ogni forma chiusa sarà esatta.

Lunghezza di una curva

Un altro tipo di integrale di linea è quello che si usa per definire la lunghezza della curva: se $C\;:\; [a,b]\;\longrightarrow\; {\bf R}^n$ è una parametrizzazione $C^1$ per la curva $X=C(t)$, allora la lunghezza può essere definita come

$$\int_C \;\frac{\dot X}{\vert\dot X\vert}\,dX= \int_a^b\; \vert\dot X(t)\vert\;dt\;;$$

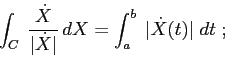
una parametrizzazione della stessa curva $X=B(s)$ tale che $\vert\dot B(s)\vert=1$ ha quindi la proprietà di avere parametro arco, cioè la lunghezza di un arco di curva coincide (a meno del segno) con l'incremento del parametro $s$.

Bibliografia :

-

Prodi, G. : Lezioni di Analisi Matematica, Parte II, Editrice Tecnico Scientifica, Pisa, 1974.

-

Stampacchia, G. : Lezioni di analisi matematica, volume secondo, Liguori Editore, Napoli, 1973.