Next: 5.4 SISTEMI LAGRANGIANI Up: 5. SISTEMI CONSERVATIVI Previous: 5.2 INTEGRABILITÀ Indice Indice analitico
Sommario Le equazioni tipiche della meccanica - e di molti altri
modelli matematici di problemi fisici - non si presentano nella forma
di equazioni di Hamilton, ma sono espresse direttamente in termini di
derivate prime e seconde delle coordinate. Tuttavia, se le equazioni
possono essere ricavate dalla definizione di una energia cinetica ed
una energia potenziale, esse possono sempre essere espresse nella
forma detta di Lagrange. Le equazioni di Lagrange possono a loro
volta, sotto certe condizioni, essere equivalenti ad equazioni di
Hamilton.
La seconda delle equazioni di Hamilton fornisce una relazione tra il momento ![]() della
coordinata q, e la sua velocità generalizzata, cioè la derivata
della
coordinata q, e la sua velocità generalizzata, cioè la derivata ![]() :
:
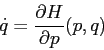
Supponiamo che la funzione ![]() sia di classe
sia di classe ![]() e
strettamente convessa, se considerata come funzione della
sola
e
strettamente convessa, se considerata come funzione della
sola ![]() , per
, per ![]() fisso. Allora la trasformazione che
esprime la
fisso. Allora la trasformazione che
esprime la ![]() in funzione della
in funzione della ![]() è monotona
crescente:
è monotona
crescente:
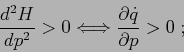
e va sotto il nome di
trasformazione di Legendre:
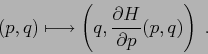
Questo è esattamente quello che abbiamo fatto nel caso
newtoniano: se
![]() , allora la seconda equazione di
Hamilton dice che
, allora la seconda equazione di
Hamilton dice che ![]() e quindi tra i due piani
e quindi tra i due piani ![]() e
e
![]() c'è una trasformazione che consiste semplicemente in un
cambiamento di scala, accompagnato dallo scambio dell'ordine degli
assi. La condizione di convessità consente di generalizzare questa
trasformazione anche nel caso in cui la relazione tra
c'è una trasformazione che consiste semplicemente in un
cambiamento di scala, accompagnato dallo scambio dell'ordine degli
assi. La condizione di convessità consente di generalizzare questa
trasformazione anche nel caso in cui la relazione tra ![]() e
e ![]() sia nonlineare.
sia nonlineare.
Ne segue che la dinamica del sistema dinamico hamiltoniano può
essere descritta anche nelle coordinate ![]() anziché
anziché
![]() . Il problema è come trasformare le equazioni di Hamilton nel
piano
. Il problema è come trasformare le equazioni di Hamilton nel
piano ![]() in equazioni che descrivano la stessa dinamica nel piano
in equazioni che descrivano la stessa dinamica nel piano
![]() .
.
Il sistema dinamico nel piano ![]() si può scrivere in modo
molto efficiente come equazione del secondo ordine:
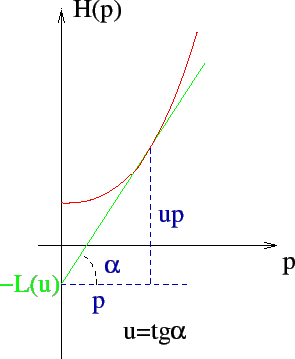
occorre definire la lagrangiana
si può scrivere in modo
molto efficiente come equazione del secondo ordine:
occorre definire la lagrangiana
![]() che può essere descritta geometricamente
come l'opposto dell'ordinata all'origine della retta tangente al grafico
dell'hamiltoniana
(si intende sempre per un valore fissato di
che può essere descritta geometricamente
come l'opposto dell'ordinata all'origine della retta tangente al grafico
dell'hamiltoniana
(si intende sempre per un valore fissato di ![]() ),
come indicato in Figura 5.4. Quindi la relazione tra
),
come indicato in Figura 5.4. Quindi la relazione tra
![]() ed
ed ![]() (indicando con
(indicando con ![]() la variabile che svolge il ruolo
di
la variabile che svolge il ruolo
di ![]() ) è data dall'equazione della tangente alla curva
) è data dall'equazione della tangente alla curva ![]() s(con
s(con ![]() fisso) che è:
fisso) che è:
 |
Si noti che se vale la condizione di convessità, per cui la
relazione tra ![]() e
e ![]() è invertibile, la formula qua sopra
può essere usata nei due sensi. Può essere la definizione di
è invertibile, la formula qua sopra
può essere usata nei due sensi. Può essere la definizione di
![]() se si conosce in modo esplicito
se si conosce in modo esplicito ![]() ; in tal caso occorre
sostituire a
; in tal caso occorre
sostituire a ![]() la sua espressione in termini di
la sua espressione in termini di ![]() . Ma se al
contrario si conosce
. Ma se al
contrario si conosce ![]() , la stessa formula definisce
, la stessa formula definisce ![]() , pur
di sostituire a
, pur
di sostituire a ![]() la sua espressione in funzione di
la sua espressione in funzione di ![]() . Questa
relazione involutiva tra le due funzioni
. Questa
relazione involutiva tra le due funzioni ![]() ed
ed ![]() si designa
con il nome di trasformata di Legendre.
si designa
con il nome di trasformata di Legendre.
Esempio:
Dobbiamo ora ricavare l'equazione di Lagrange, che esprime
- in termini della funzione di Lagrange - la dinamica nel piano
![]() . Calcoliamo le derivate parziali della funzione di
Lagrange, tenendo conto della dipendenza di
. Calcoliamo le derivate parziali della funzione di
Lagrange, tenendo conto della dipendenza di ![]() sia da
sia da ![]() che da
che da ![]() per effetto della inversa della trasformazione di Legendre:
per effetto della inversa della trasformazione di Legendre:
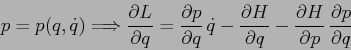
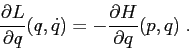
Si intende che la relazione qui sopra vale con i due membri calcolati nei punti corrispondenti - per la trasformazione di Legendre - nei due piani.
In modo analogo
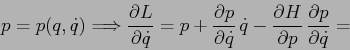
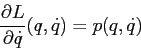
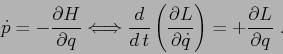
In conclusione le equazioni di Hamilton nel piano ![]() ,
e l'equazione di Lagrange nel piano
,
e l'equazione di Lagrange nel piano ![]() :
:
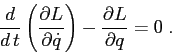
L'equazione di Lagrange è un'equazione differenziale del secondo
ordine; per ricavare il corrispondente sistema dinamico nel piano
![]() occorre considerare che il momento
occorre considerare che il momento ![]() è funzione di
è funzione di ![]() ,
quindi
,
quindi
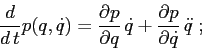
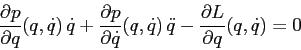
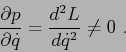
La condizione di non annullamento della derivata seconda della
funzione di Lagrange rispetto a ![]() è la condizione di
convessità che assicura che l'inversa della trasformazione di
Legendre è monotona crescente. Quindi tale condizione è
equivalente alla condizione di convessità su
è la condizione di
convessità che assicura che l'inversa della trasformazione di
Legendre è monotona crescente. Quindi tale condizione è
equivalente alla condizione di convessità su ![]() come funzione di
come funzione di
![]() , cioè al non annullamento della derivata seconda della funzione
di Hamilton rispetto a
, cioè al non annullamento della derivata seconda della funzione
di Hamilton rispetto a ![]() .
.
Esempio:
Esercizio Date le hamiltoniane scrivere la corrispondente lagrangiana e l'equazione di Lagrange.
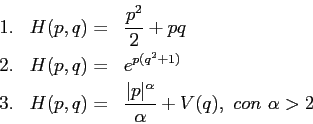
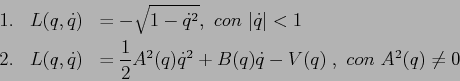
La coordinata ![]() parametrizza lo spazio delle configurazioni, ma
naturalmente la scelta di un altra coordinata è possibile.
Supponiamo che
parametrizza lo spazio delle configurazioni, ma
naturalmente la scelta di un altra coordinata è possibile.
Supponiamo che ![]() sia un cambiamento di coordinata, espresso da
una funzione differenziabile, invertibile e con inversa differenziabile;
questo implica che la derivata
sia un cambiamento di coordinata, espresso da
una funzione differenziabile, invertibile e con inversa differenziabile;
questo implica che la derivata ![]() . Supponiamo che la
funzione di Lagrange
. Supponiamo che la
funzione di Lagrange ![]() si trasformi in
si trasformi in
![]() , nel
senso che le due funzioni hanno lo stesso valore nei punti
corrispondenti:
, nel
senso che le due funzioni hanno lo stesso valore nei punti
corrispondenti:
Sia ![]() un cambiamento di coordinata (con
un cambiamento di coordinata (con ![]() ) di
classe
) di
classe ![]() ; sia
; sia
![]() . Allora l'equazione di
Lagrange nelle variabili
. Allora l'equazione di
Lagrange nelle variabili ![]() , e l'equazione di Lagrange nella variabile
, e l'equazione di Lagrange nella variabile ![]() ,
esprimono dinamiche equivalenti:
,
esprimono dinamiche equivalenti:
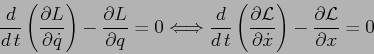
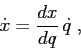
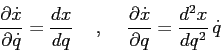
È nel calcolo di queste derivate parziali che si sfrutta
l'ipotesi che ![]() sia
sia ![]() .
.
Per trovare la formula di trasformazione dell'equazione di Lagrange
basta usare le derivate di funzioni composte: per il momento ![]() coniugato
alla coordinata
coniugato
alla coordinata ![]()
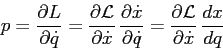
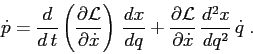
Per completare l'espressione dell'equazione di Lagrange nella ![]() in
termini della funzione trasformata
in
termini della funzione trasformata ![]() occorre calcolare anche
l'altra derivata:
occorre calcolare anche
l'altra derivata:
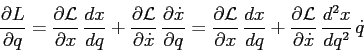
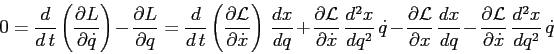
![\begin{displaymath}
\left[\frac d{d\,t}\left(\frac{\partial {\cal L}}{\partial {...
...rtial {\cal L}}{\partial {x}}\right]\, \frac{d{x}}{d{q}} =0\;.
\end{displaymath}](img1687.png)
La legge di trasformazione a cui soddisfano le equazioni di Lagrange è la stessa a cui soddisfano i gradienti e si chiama covariante, da cui il nome del teorema.
Esercizio
Data la lagrangiana