Next: 1.2 SISTEMI LINEARI, INTEGRABILITÀ Up: 1. DEFINIZIONI E PRIMI Previous: 1. DEFINIZIONI E PRIMI Indice Indice analitico
Sommario Un sistema dinamico esprime la variabilità di uno stato
nel tempo. Lo stato è rappresentato da un punto in uno spazio
vettoriale di dimensione n. Il tempo può essere
rappresentato come continuo, ![]() , oppure discreto,
, oppure discreto, ![]() .
Il sistema dinamico è la legge che esprime la variazione nel
tempo, la sua soluzione è l'insieme delle orbite, in
funzione delle condizioni iniziali.
.
Il sistema dinamico è la legge che esprime la variazione nel
tempo, la sua soluzione è l'insieme delle orbite, in
funzione delle condizioni iniziali.
Definizione:
Un'orbita di un sistema dinamico continuo è una funzione
![]() della variabile continua
della variabile continua ![]() a valori in
a valori in ![]() che soddisfa identicamente, per ogni
che soddisfa identicamente, per ogni ![]() , all'equazione
differenziale, cioè se si sostituisce:
, all'equazione
differenziale, cioè se si sostituisce:
Definizione:
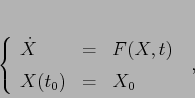
![\begin{displaymath}
Y=\left[\begin{array}{c}{t}\\
{X}\end{array}\right]\hspace...
...}={\left[\begin{array}{c}{t_0}\\
{X_0}\end{array}\right]}\;.
\end{displaymath}](img62.png)
Definizione:
Un'orbita di un sistema dinamico
discreto è una funzione
![]() della variabile
discreta
della variabile
discreta ![]() a valori in
a valori in ![]() che soddisfa, per ogni
che soddisfa, per ogni ![]() :
:
Il sistema dinamico è definito dalla legge che governa il
cambiamento, cioè dal campo vettoriale ![]() o dalla mappa
o dalla mappa ![]() , non
dalle orbite, anche se ovviamente date tutte le orbite si può
ricostruire il sistema dinamico; viceversa non è in generale
facile trovare tutte le orbite di un sistema dinamico dato.
, non
dalle orbite, anche se ovviamente date tutte le orbite si può
ricostruire il sistema dinamico; viceversa non è in generale
facile trovare tutte le orbite di un sistema dinamico dato.
Interpretare la variabile indipendente ![]() di un sistema
dinamico continuo come tempo è abbastanza naturale, ma non
è obbligatorio. Anche l'indice
di un sistema
dinamico continuo come tempo è abbastanza naturale, ma non
è obbligatorio. Anche l'indice ![]() della successione che risolve
un sistema dinamico discreto può indicare un tempo, sia inteso
come approssimazione di un tempo continuo, sia perché lo stato ha
senso solo a intervalli discreti di tempo (per esempio ogni giorno
lavorativo nel caso di variabili economiche).
della successione che risolve
un sistema dinamico discreto può indicare un tempo, sia inteso
come approssimazione di un tempo continuo, sia perché lo stato ha
senso solo a intervalli discreti di tempo (per esempio ogni giorno
lavorativo nel caso di variabili economiche).
Si usa la parola soluzione per indicare una curva ![]() che soddisfa all'equazione di un sistema dinamico continuo solo per
valori di
che soddisfa all'equazione di un sistema dinamico continuo solo per
valori di ![]() in un intervallo aperto. Non è detto a priori che un
sistema dinamico continuo abbia soluzioni definite per ogni
in un intervallo aperto. Non è detto a priori che un
sistema dinamico continuo abbia soluzioni definite per ogni
![]() , che quindi costituiscano delle orbite; una soluzione
, che quindi costituiscano delle orbite; una soluzione ![]() (oppure
(oppure ![]() ) potrebbe uscire da
) potrebbe uscire da ![]() o andare all'infinito, per
o andare all'infinito, per
![]() finito (oppure
finito (oppure ![]() finito). Le condizioni per cui ogni punto di
finito). Le condizioni per cui ogni punto di
![]() appartiene ad un'orbita nel caso continuo saranno discusse
nell'appendice A.5.
appartiene ad un'orbita nel caso continuo saranno discusse
nell'appendice A.5.
Nel caso discreto, poiché per definizione l'applicazione ![]() è iniettiva e surgettiva su
è iniettiva e surgettiva su ![]() , per ogni
, per ogni ![]() esiste
un'orbita definita da:
esiste
un'orbita definita da:
Nelle ipotesi qui fatte ogni sistema dinamico è tale che, per
ogni condizione iniziale ![]() , l'orbita tale che
, l'orbita tale che ![]() se esiste è unica. Questo è ovvio nel caso discreto, è invece
un risultato significativo nel caso continuo, che sarà dimostrato
nell'appendice A.5.
se esiste è unica. Questo è ovvio nel caso discreto, è invece
un risultato significativo nel caso continuo, che sarà dimostrato
nell'appendice A.5.
Andrea Milani 2009-06-01