Next: 5.3 TRASFORMATA DI LEGENDRE Up: 5. SISTEMI CONSERVATIVI Previous: 5.1 SISTEMI NEWTONIANI E Indice Indice analitico
Sommario I sistemi hamiltoniani ad un grado di libertà sono
integrabili nel senso che la soluzione si
può esprimere mediante un algoritmo che include quadrature e
funzioni implicite. Tutte le curve di livello regolari, semplici e
chiuse della funzione hamiltoniana corrispondono ad orbite
periodiche.
Consideriamo una hamiltoniana del tipo che si può ottenere da un
sistema newtoniano, e le corrispondenti equazioni di Hamilton:
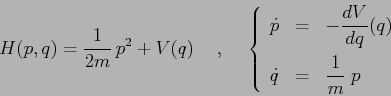
Poiché la funzione di Hamilton è un integrale primo, se si fissa
il suo valore ![]() l'equazione della curva di livello
l'equazione della curva di livello ![]() definisce implicitamente una relazione tra
definisce implicitamente una relazione tra ![]() e
e ![]() : per esempio si
può ricavare
: per esempio si
può ricavare ![]() in funzione di
in funzione di ![]() :
:
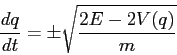
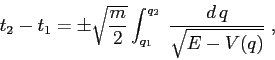
 |
La soluzione del sistema dinamico però richiede la
legge oraria
del moto, cioè la relazione ![]() , che è espressa dalla
funzione inversa. L'esistenza della funzione inversa richiede che la
funzione
, che è espressa dalla
funzione inversa. L'esistenza della funzione inversa richiede che la
funzione ![]() sia monotona, cioè che
sia monotona, cioè che ![]() non cambi di
segno. Perciò, se una curva di livello
non cambi di
segno. Perciò, se una curva di livello ![]() passa per un punto
passa per un punto
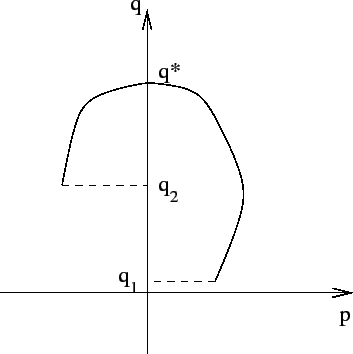
![]() (come in Figura 5.1) il tempo necessario
perché la soluzione vada da
(come in Figura 5.1) il tempo necessario
perché la soluzione vada da ![]() con
con ![]() a
a ![]() con
con ![]() passando per
passando per ![]() sarà dato dalla somma di due
integrali:
sarà dato dalla somma di due
integrali:
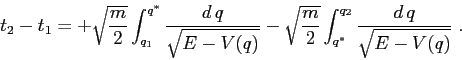
Quindi il sistema è integrabile nel senso che la soluzione è definita da equazioni finite (non contenenti le derivate) che però possono coinvolgere una funzione implicita, una quadratura e una funzione inversa.
Il caso più importante dell'applicazione di questo procedimento di
calcolo della legge oraria ``a tratti'' è quello del calcolo dei
periodi. Un punto di equilibrio di un sistema hamiltoniano
è un punto in cui si annullano i due secondi membri delle equazioni
di Hamilton, cioè un punto in cui
![]() ; quindi
è anche un punto stazionario della funzione hamiltoniana. Nel caso
delle hamiltoniane
; quindi
è anche un punto stazionario della funzione hamiltoniana. Nel caso
delle hamiltoniane
![]() questo può verificarsi solo
per
questo può verificarsi solo
per ![]() , nei punti
, nei punti ![]() tali che
tali che ![]() .
.
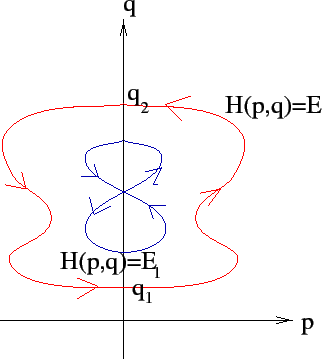 |
Supponiamo che la curva di livello ![]() non contenga alcun punto
di equilibrio; allora nei punti in cui la curva attraversa la retta
non contenga alcun punto
di equilibrio; allora nei punti in cui la curva attraversa la retta
![]() si ha
si ha ![]() , ma
, ma ![]() , cioè la retta
, cioè la retta ![]() viene
attraversata trasversalmente. Siano
viene
attraversata trasversalmente. Siano ![]() due valori di
due valori di
![]() tali che
tali che ![]() , e tali che nell'intervallo
, e tali che nell'intervallo ![]() vale sempre
vale sempre ![]() . Allora esistono due curve
. Allora esistono due curve
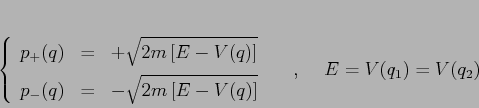
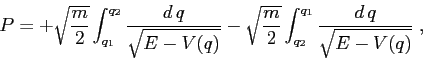
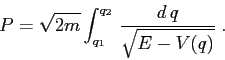
L'integrale che fornisce il periodo è un integrale
improprio in tutti e due gli estremi, poiché
![]() . Se però
. Se però ![]() ,
espandendo in
,
espandendo in ![]() la funzione integranda è
la funzione integranda è
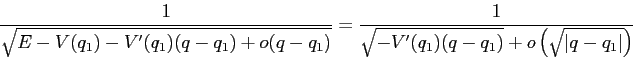
Se invece l'insieme di livello contiene un punto di equilibrio, come
nella Figura 5.2 accade per ![]() , allora questo
potrà essere punto limite per
, allora questo
potrà essere punto limite per ![]() , oppure per
, oppure per ![]() (o anche in entrambi i casi), delle orbite contenute nell'insieme
di livello; l'immagine di ogni orbita sarà una componente connessa
dell'insieme di livello privato dei punti di equilibrio.
(o anche in entrambi i casi), delle orbite contenute nell'insieme
di livello; l'immagine di ogni orbita sarà una componente connessa
dell'insieme di livello privato dei punti di equilibrio.
Esempio:
La formula del periodo data mediante quadrature è
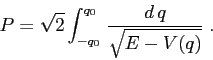
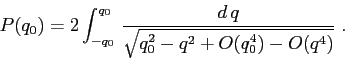
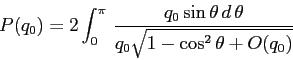
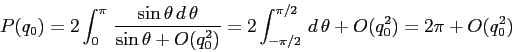
In effetti il limite per ![]() andrebbe discusso
con qualche precauzione, visto che si tratta di un
integrale improprio con parametro; il passaggio al limite
è legittimo perché l'integrale improprio resta sempre convergente.
andrebbe discusso
con qualche precauzione, visto che si tratta di un
integrale improprio con parametro; il passaggio al limite
è legittimo perché l'integrale improprio resta sempre convergente.
Esercizio
Studiare i sistemi dinamici ottenuti dalle hamiltoniane somma di
un'energia cinetica ![]() (con
(con ![]() ) e di un'energia
potenziale cubica
) e di un'energia
potenziale cubica
![]() , con
, con ![]() parametri reali.
parametri reali.
Suggerimento: Se ![]() , eseguire una traslazione
, eseguire una traslazione
![]() scegliendo la costante
scegliendo la costante ![]() in modo da annullare il termine
quadratico.
in modo da annullare il termine
quadratico.
Questa discussione si generalizza ad una funzione
hamiltoniana ![]() qualsiasi, anche se
non deriva da un sistema newtoniano:
qualsiasi, anche se
non deriva da un sistema newtoniano:
Sia ![]() una funzione hamiltoniana di classe
una funzione hamiltoniana di classe ![]() su di un
aperto
su di un
aperto
![]() . Se una
componente connessa
. Se una
componente connessa
![]() dell'insieme di livello
dell'insieme di livello ![]() è non vuota,
compatta, e non contiene punti stazionari di
è non vuota,
compatta, e non contiene punti stazionari di
![]() , allora coincide con la traiettoria di
un'orbita periodica.
Se invece
, allora coincide con la traiettoria di
un'orbita periodica.
Se invece ![]() contiene dei punti stazionari isolati,
allora ogni componente connessa di
contiene dei punti stazionari isolati,
allora ogni componente connessa di ![]() privata dei punti stazionari
è una traiettoria; la soluzione corrispondente o esce da ogni
compatto in
privata dei punti stazionari
è una traiettoria; la soluzione corrispondente o esce da ogni
compatto in ![]() oppure ha come punto limite uno dei punti stazionari
(questo vale sia per
oppure ha come punto limite uno dei punti stazionari
(questo vale sia per ![]() , sia per
, sia per ![]() ).
Dimostrazione:
).
Dimostrazione:
Se invece ![]() contiene dei punti stazionari, sia
contiene dei punti stazionari, sia ![]() l'insieme
formato da
l'insieme
formato da ![]() privato dei punti stazionari.
privato dei punti stazionari. ![]() è localmente una
curva regolare, e quindi ogni sua componente connessa per archi
contiene solo punti appartenenti ad una sola traiettoria.
è localmente una
curva regolare, e quindi ogni sua componente connessa per archi
contiene solo punti appartenenti ad una sola traiettoria.
I punti di minimo dell'hamiltoniana sono circondati da curve di
livello chiuse, sulle quali le orbite periodiche girano in senso
antiorario (infatti ![]() è rivolto verso l'esterno delle curve
di livello, e
è rivolto verso l'esterno delle curve
di livello, e ![]() è ruotato di
è ruotato di ![]() ). Questo caso era
già noto per una hamiltoniana proveniente da un sistema newtoniano
con un minimo dell'energia potenziale. Se invece la hamiltoniana ha un
massimo (caso che non si presenta nei sistemi newtoniani) le orbite
periodiche vicine girano in senso orario.
). Questo caso era
già noto per una hamiltoniana proveniente da un sistema newtoniano
con un minimo dell'energia potenziale. Se invece la hamiltoniana ha un
massimo (caso che non si presenta nei sistemi newtoniani) le orbite
periodiche vicine girano in senso orario.
Anche il procedimento per calcolare la legge oraria si
generalizza ad una funzione hamiltoniana qualsiasi. Sia ![]() una
funzione hamiltoniana di classe
una
funzione hamiltoniana di classe ![]() su di un aperto
su di un aperto
![]() . Se
. Se
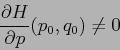
![\begin{displaymath}
t(q)=\int_{q_0}^q \; \left[{\frac{\partial {H}}{\partial {p}} (p(q'),q')}\right]^{-1}\; {d\,q'}\;,
\end{displaymath}](img1626.png)
Quando la curva ![]() passa per un punto in cui
passa per un punto in cui
![]() , allora
, allora ![]() , e la quadratura che serve a
calcolare la legge oraria viene spezzata in due integrali; in
particolare questo è sempre necessario per calcolare il periodo di
un'orbita periodica, visto che
, e la quadratura che serve a
calcolare la legge oraria viene spezzata in due integrali; in
particolare questo è sempre necessario per calcolare il periodo di
un'orbita periodica, visto che ![]() avrà sempre sull'orbita stessa
almeno un punto di massimo ed un punto di minimo (in cui
avrà sempre sull'orbita stessa
almeno un punto di massimo ed un punto di minimo (in cui ![]() ).
).
Oltre a descrivere le soluzioni mediante quadrature e funzioni inverse, possiamo studiarne le proprietà qualitative.
Per studio delle proprietà qualitative si intende: trovare i punti di equilibrio,
determinare eventuali orbite periodiche, individuare le orbite aperte
ma definite per ogni ![]() , disegnare approssimativamente le
separatrici, le curve eccezionali, e alcune soluzioni rappresentative
descrivendone gli insiemi limite.
, disegnare approssimativamente le
separatrici, le curve eccezionali, e alcune soluzioni rappresentative
descrivendone gli insiemi limite.
I punti di equlibrio corrispondono ai
punti stazionari
della hamiltoniana, ed il sistema
linearizzato si ottiene dalla matrice hessiana
![\begin{displaymath}
\frac{\partial^2 {H}}{\partial {(p,q)}^2}= A= \left[\begin{array}{cc}{a}&{b}\\
{b}&{d}\end{array}\right]
\end{displaymath}](img1631.png)
![\begin{displaymath}
J\, A= \left[\begin{array}{cc}{0}&{-1}\\
{1}&{\phantom{-}0...
...}{-b}&{-d}\\
{\phantom{-}a}&{\phantom{-}b}\end{array}\right]
\end{displaymath}](img1632.png)
L'unico passaggio delicato di questo studio qualitativo è quello in
cui si decide quali insiemi di livello ![]() sono compatti: in tal
caso se non ci sono punti stazionari l'insieme di livello è unione
di componenti connesse che corrispondono ad orbite periodiche, se ci
sono punti di equilibrio essi costituiranno gli insiemi limite. Se
invece l'insieme di livello è illimitato, o comunque esce da ogni
compatto contenuto nell'insieme di definizione di
sono compatti: in tal
caso se non ci sono punti stazionari l'insieme di livello è unione
di componenti connesse che corrispondono ad orbite periodiche, se ci
sono punti di equilibrio essi costituiranno gli insiemi limite. Se
invece l'insieme di livello è illimitato, o comunque esce da ogni
compatto contenuto nell'insieme di definizione di ![]() , almeno una
delle componenti connesse è una curva aperta, cioè
parametrizzata in modo iniettivo da un intervallo aperto (per esempio
usando il tempo come parametro).
, almeno una
delle componenti connesse è una curva aperta, cioè
parametrizzata in modo iniettivo da un intervallo aperto (per esempio
usando il tempo come parametro).
Esempio:
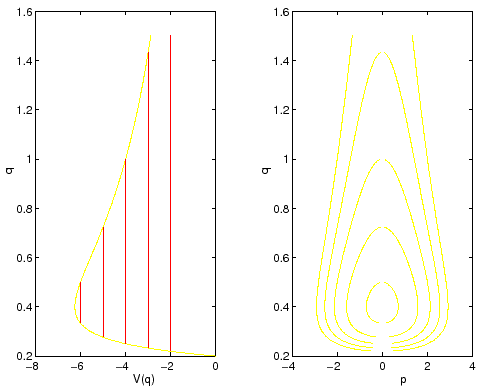 |
Se invece
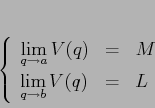
Esercizio
Dati i sistemi dinamici le cui equazioni di Newton sono della forma:
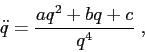
Esercizio
Studiare il sistema dinamico definito dalla hamiltoniana (già usata
come esempio nella Sezione 5.1)
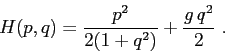
Andrea Milani 2009-06-01