Next: 3.2 POZZI E SORGENTI Up: 3. TEORIA QUALITATIVA Previous: 3. TEORIA QUALITATIVA Indice Indice analitico
Sommario Un sistema dinamico continuo ha una soluzione per
ogni condizione iniziale; se per ogni ![]() essa resta in un
compatto, allora avrà senso chiedersi quale ne sia il limite per
essa resta in un
compatto, allora avrà senso chiedersi quale ne sia il limite per
![]() . Se una soluzione ha un limite finito per
. Se una soluzione ha un limite finito per
![]() , questo limite sarà un punto di equilibrio. Un punto di
equilibrio è considerato stabile se tutte le soluzioni ad essa
vicine restano vicine, asintoticamente stabile se esse hanno anche lo
stesso limite.
, questo limite sarà un punto di equilibrio. Un punto di
equilibrio è considerato stabile se tutte le soluzioni ad essa
vicine restano vicine, asintoticamente stabile se esse hanno anche lo
stesso limite.
Un sistema dinamico continuo ![]() , con
, con ![]() una funzione
una funzione
![]() regolare (di classe almeno
regolare (di classe almeno ![]() ) su un aperto
) su un aperto
![]() , ammette sempre una ed una sola soluzione che passa
per la condizione iniziale
, ammette sempre una ed una sola soluzione che passa
per la condizione iniziale ![]() (per il teorema di
esistenza e unicità). Un caso
particolarmente semplice si verifica quando
(per il teorema di
esistenza e unicità). Un caso
particolarmente semplice si verifica quando
![]() :
:
Definizione:
Per il teorema di esistenza e unicità
tale soluzione è unica, quindi un'altra soluzione non
può entrare (o uscire) dal punto di equilibrio. In molti
esempi, come nei punti di tipo nodo oppure
fuoco, esistono soluzioni che si avvicinano sempre di
più ad un punto di equilibrio, o per ![]() o per
o per
![]() , ma non arrivano a coincidere con esso
per nessun
, ma non arrivano a coincidere con esso
per nessun ![]() finito.
finito.
Il teorema di esistenza e unicità in generale non garantisce
l'esistenza di un'orbita, definita per ogni ![]() , ma solo una
soluzione definita per valori di
, ma solo una
soluzione definita per valori di ![]() in un intorno dello zero. Le
soluzioni possono essere espresse collettivamente mediante il
flusso integrale, che però in generale non è definito per
ogni
in un intorno dello zero. Le
soluzioni possono essere espresse collettivamente mediante il
flusso integrale, che però in generale non è definito per
ogni ![]() , e neppure per ogni condizione iniziale
, e neppure per ogni condizione iniziale
![]() per
un
per
un ![]() fissato: infatti l'intervallo su cui ogni soluzione è
definita dipende dalla condizione iniziale:
fissato: infatti l'intervallo su cui ogni soluzione è
definita dipende dalla condizione iniziale:
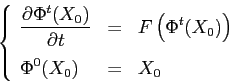
Il teorema di continuazione delle soluzioni assicura che
la soluzione non cessa di essere definita ad un tempo finito ![]() , a
meno che per
, a
meno che per ![]() la soluzione stessa non tenda verso la
frontiera di
la soluzione stessa non tenda verso la
frontiera di ![]() (in un senso che viene precisato nella
sezione A.5). Perciò se una soluzione
resta limitata ``per sempre'' (diciamo per ogni
(in un senso che viene precisato nella
sezione A.5). Perciò se una soluzione
resta limitata ``per sempre'' (diciamo per ogni ![]() ) ha
senso chiedersi quale ne sia il limite per
) ha
senso chiedersi quale ne sia il limite per ![]() .
.
Se la soluzione ![]() ha limite per
ha limite per ![]() :
:
Dimostrazione:
La stabilità è un concetto base nella teoria dei sistemi dinamici, e forse proprio per questo ne esistono molte diverse definizioni. Qui presentiamo solo i due tipi principali di stabilità per un punto di equilibrio di un sistema dinamico continuo.
Definizione:
Esempio:
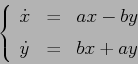
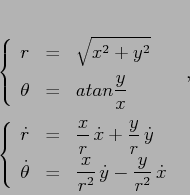
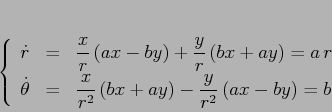
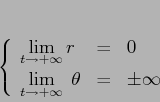
La coordinata polare ![]() non è definita in ogni caso dalla
funzione arcotangente, che assume solo valori tra
non è definita in ogni caso dalla
funzione arcotangente, che assume solo valori tra ![]() e
e
![]() . In effetti
. In effetti ![]() è una variabile angolo,
cioè è definita solo a meno di multipli di
è una variabile angolo,
cioè è definita solo a meno di multipli di ![]() ; però la
derivata totale di
; però la
derivata totale di ![]() è ben definita per ogni punto diverso
dall'origine (i calcoli eseguiti qui sopra sono quindi corretti).
è ben definita per ogni punto diverso
dall'origine (i calcoli eseguiti qui sopra sono quindi corretti).
Definizione:
![]() stesso appartiene sempre al suo bacino.
stesso appartiene sempre al suo bacino. ![]() è attrattivo
se e solo se sta nella parte interna del suo bacino di
attrazione. Anche un punto non attrattivo può avere un bacino
di attrazione, come nel caso della sella instabile.
è attrattivo
se e solo se sta nella parte interna del suo bacino di
attrazione. Anche un punto non attrattivo può avere un bacino
di attrazione, come nel caso della sella instabile.
Esempio:
Definizione:
Si noti che l'intorno ![]() dipende dalla scelta di
dipende dalla scelta di ![]() , cioè
tutte le soluzioni che partono vicino a
, cioè
tutte le soluzioni che partono vicino a ![]() restano in un suo
intorno arbitrariamente piccolo, ma a condizione di avere condizione
iniziale adeguatamente vicina.
restano in un suo
intorno arbitrariamente piccolo, ma a condizione di avere condizione
iniziale adeguatamente vicina.
Un punto stabile deve essere di equilibrio: se così non
fosse, prendiamo un punto ![]() sulla stessa soluzione, cioè con
sulla stessa soluzione, cioè con
![]() . Allora esiste un intorno
. Allora esiste un intorno ![]() di
di ![]() che non contiene
che non contiene
![]() ; qualunque sia l'intorno
; qualunque sia l'intorno ![]() di
di ![]() , esso contiene
, esso contiene ![]() , e ogni
soluzione passante per
, e ogni
soluzione passante per ![]() non può stare definitivamente in
non può stare definitivamente in ![]() perché se per
perché se per ![]() passa per
passa per ![]() , per
, per ![]() passa per
passa per ![]() che non
è in
che non
è in ![]() .
.
Un punto stabile e attrattivo si dice asintoticamente stabile.
Un punto attrattivo non è necessariamente stabile, ma i controesempi non sono semplici.
Esempio:
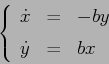
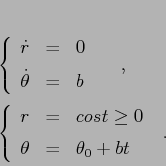
Definizione:
Assegnato l'intorno ![]() , l'intorno
, l'intorno ![]() è scelto
arbitrariamente piccolo, eppure alcune soluzioni che
partono da
è scelto
arbitrariamente piccolo, eppure alcune soluzioni che
partono da ![]() finiscono con l'uscire da
finiscono con l'uscire da ![]() .
.
Esempio:
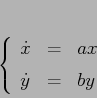
Problema
Sia ![]() una matrice
una matrice ![]() con autovalori che hanno tutti parte
reale nulla. Provare che per il sistema dinamico lineare
con autovalori che hanno tutti parte
reale nulla. Provare che per il sistema dinamico lineare ![]() l'origine è un punto stabile se e solo se
l'origine è un punto stabile se e solo se ![]() è una
matrice semisemplice.
(Soluzione)
è una
matrice semisemplice.
(Soluzione)
Gli esempi qui sopra sono sistemi dinamici lineari, dei quali è possibile scrivere esplicitamente le soluzioni; perciò lo studio del comportamento qualitativo delle soluzioni, come per esempio la stabilità, è banale. Al contrario, le definizioni qualitative come la stabilità diventano uno strumento essenziale quando si ha a che fare con un sistema dinamico nonlineare.
Andrea Milani 2009-06-01