3.3 FUNZIONI DI LYAPOUNOV

Sommario La stabilità di un punto di equilibrio può essere determinata mediante le proprietà di una funzione di Lyapounov, che generalizza le proprietà della distanza nell'intorno di un pozzo e dell'energia in un sistema dissipativo.

Derivata totale

Consideriamo un sistema dinamico continuo $\dot X = F(X)$ con il campo vettoriale $F$ definito e $C^1$ su di un aperto $W\subset{\bf R}^n$.

Definizione:

Data una funzione $V(X)$ definita e di classe $C^1$ in $W$, si dice derivata totale di $V$ (rispetto al campo vettoriale $F(X)$) la funzione:

$$\dot V(X)= \frac{d{V}}{d{t}}(X)= grad\, V(X) \cdot F(X)$$


Se $\Phi^t(X)$ è il flusso integrale di $F(X)$, per il teorema di derivazione delle funzioni composte la derivata totale è la derivata in $t=0$ della funzione di $t$ ottenuta fissando la condizione iniziale:

$$h(t)=V\left(\Phi^t(X)\right) \hspace{5mm},\hspace{5mm} \frac{d{h}}{d{t}}(0)= grad\, V(X) \cdot F(X) =\dot V(X)$$


La derivata totale esprime la variazione nel tempo di una funzione, e può essere utilizzata sia per calcoli quantitativi che per studiare le proprietà qualitative come la stabilità. La notazione con il punto è consistente con quella già adottata per il vettore $X$ stesso: $\dot X$ è la derivata totale del vettore $X$.

Il metodo della funzione di Lyapounov

Definizione:

Una funzione $V$ definita e di classe $C^1$ in un intorno $U$ (si intende che $U\subset W$) di un punto di equilibrio $S$ si dice funzione di Lyapounov per l'equilibrio $S$ se valgono le due condizioni:

(a)
$\dot V(X) \leq 0$ per ogni $X$ in $U$.

(b)
$V(S)=0$ e $V(X)>0$ per ogni $X$ in $U$ escluso $S$.

La funzione di Lyapounov ha un minimo forte in corrispondenza del punto di equilibrio (per convenienza si fissa il valore del minimo a zero), e derivata totale mai positiva al di fuori del minimo, quindi il valore della funzione non cresce lungo le soluzioni.

Se vale la proprietà (b) e anche

(c)

$\dot V(X) < 0$ per ogni $X$ in $U$ escluso $S$

allora $V$ si dice funzione di Lyapounov stretta Una funzione di Lyapounov stretta è strettamente decrescente su ogni soluzione del sistema dinamico.

Esempio:

Sia $S$ un pozzo: come visto nella dimostrazione del teorema del pozzo nonlineare esiste una norma $\vert\vert X\vert\vert _Z$, associata ad una base $Z$ dei vettori $X-S$, tale che:

$$\frac{d{ }}{d{t}} \, \vert\vert X-S\vert\vert _Z \leq -c\, \vert\vert X-S\vert\vert _Z\leq 0$$


per ogni $X$ in un intorno $U$ di $S$, e con $-c$ una costante negativa. Perciò $V(X)=\vert\vert X-S\vert\vert^2_Z$ è una funzione di Lyapounov.

Se il punto di equilibrio $S$ possiede, in un intorno $U$, una funzione di Lyapounov $V(X)$, allora è stabile.

Dimostrazione:

Prendiamo la palla aperta:

$$B_\delta = \{ X :\; \vert\vert X-S\vert\vert<\delta\}$$


la cui frontiera è la sfera

$$S_\delta = \{ X :\; \vert\vert X-S\vert\vert=\delta\}$$


con $\delta$ abbastanza piccolo perché sia $B_\delta \subset U$ e $S_\delta\subset U$. Poiché $S_\delta$ è un compatto, per il teorema di Weierstrass esiste il minimo $m$ di $V(X)$ su $S_\delta$, e vale $m>0$. Consideriamo l'intorno $Q$ di $S$ definito da:

$$Q=\{X\in B_\delta:\; V(X)< m\} \ .$$


Le soluzioni che partono da una condizione iniziale $X$ in $Q$ non possono mai passare da un punto di $S_\delta$, perché su di esse il valore iniziale di $V$ è minore di $m$, e la funzione $V$ non può crescere lungo l'orbita. La distanza da $S$ lungo la soluzione è una funzione continua del tempo, quindi non può diventare $> \delta$ senza passare dal valore $\delta$, cioè una soluzione con condizioni iniziali in $Q$, non potendo attraversare $S_\delta$ non può uscire da $B_\delta$.

Questo è vero per tutti i $\delta >0$ abbastanza piccoli, gli insiemi $B_\delta$ sono un sistema fondamentale di intorni, quindi la definizione di stabilità è soddisfatta.

 C.D.D.

Esempio:

Consideriamo il sistema dinamico in $R^2$:

$$\left\{\begin{array}{lcl} {\displaystyle \dot x} & {\disp... ...y} & {\displaystyle=} &{\displaystyle -x} \end{array}\right.$$


(equazione di Lienard). Se prendiamo una funzione $f(x)$ dispari e positiva per $x>0$, l'origine è stabile. Infatti possiamo usare come funzione di Lyapounov

$$V(x,y)=\frac 12\,(x^2+y^2)\ ; \ \ \dot V = x\,\dot x + y\,\dot y= x\,(y-f(x))+y\,(-x)=-x\,f(x)\leq 0$$

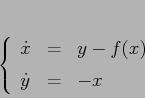
Esercizio Studiare la stabilità dell'origine per il sistema

$$\frac d{d\,t}{\left[\begin{array}{c}{x}\\ {y}\end{array}\r... ...}=\left[\begin{array}{c}{-y-x^3}\\ {x}\end{array}\right] \;.$$

(Soluzione)

Funzione di Lyapounov decrescente

Se una funzione con la proprietà (a) della funzione di Lyapounov è definita globalmente, cioè su tutto $W$, è possibile ottenere informazioni sui bacini di attrazione dei vari punti di equilibrio. A questo scopo occorre introdurre la nozione di insieme invariante per il flusso.

Definizione:

Un insieme $P$, contenuto nell'insieme $W$ su cui è definito un sistema dinamico continuo, si dice positivamente invariante se per ogni $X_0$ in $P$ la soluzione con condizione iniziale $X_0$ esiste per ogni $t>0$ ed è contenuta in $P$:

$$X_0\in P \Longrightarrow \Phi^t(X_0)\in P\ , t\geq 0$$


Un insieme $P$ è invariante per il flusso integrale se le soluzioni con condizione iniziale in $P$, per ogni $t$ in ${\bf R}$, esistono e sono contenute in $P$.

Sia $S$ un punto di equilibrio per un sistema dinamico continuo definito sull'aperto $W,$ e sia $V(X)$ una funzione di Lyapounov per $S$, definita su tutto $W.$ Se $P$ è un intorno di $S$ contenuto in $W,$ compatto e positivamente invariante, tale che su ogni semiorbita contenuta in $P$ la funzione $V$ sia strettamente decrescente (salvo che su $S$), allora $S$ è asintoticamente stabile e $P$ è contenuto nel bacino di $S$.

La condizione che $V$ sia decrescente è certamente soddisfatta se $V$ è una funzione di Lyapounov stretta. Però l'ipotesi usata in questo teorema è assi più generale: vedremo nel caso del sistema dissipativo a un grado di libertà che questa generalizzazione è utile. Esiste una versione ancora più generale del teorema, in cui si usa soltanto l'ipotesi che la funzione di Lyapounov non sia costante su alcuna traiettoria, salvo che su $S$; si veda [Hirsch-Smale 74], Capitolo 9.

Dimostrazione:

Prendiamo una condizione iniziale nell'insieme $P$ di cui nelle ipotesi; la soluzione $X(t)$ non può lasciare il compatto $P$ per $t>0$, quindi esiste in $P$ almeno un valore limite $Y_0$ di $X(t)$ per $t\to\infty$. Sia $t_m$ una successione di valori di $t$, con $t_m\to +\infty$ per $m\to +\infty$, tale che

$$\lim_{m\to+\infty}\, X(t_m)=Y_0 \hspace{5mm},\hspace{5mm}\lim_{m\to+\infty}\, V(X(t_m))= V(Y_0)$$


(la prima per definizione di valore limite, la seconda per la continuità della funzione $V$). Se però $Y_0\neq S$ esiste una soluzione $Y(t)$ che ha per condizione iniziale $Y_0$, lungo la quale $V(Y(t))$ è strettamente decrescente per ipotesi: quindi per $s>0$, $V(Y(s))<V(Y_0)$.

Se allora scegliamo un $m$ abbastanza grande, in modo che $X(t_m)$ sia abbastanza vicino ad $Y_0$, per la continuità del flusso $X(t_m+s)$ sarà abbastanza vicino ad $Y(s)$ e per il teorema di permanenza del segno la funzione continua $V$ soddisferà a $V(X(t_m+s))<V(Y_0)$. Ma allora la soluzione $X(t)$ per $t>t_m+s$ non può ripassare arbitrariamente vicino a $Y_0$, perché questo contraddice la decrescenza di $V(X(t))$. Ne segue che $Y_0$ non può essere un valore limite ed essere diverso da $S$ e che $S$ è il limite. Quindi $S$ è attrattivo, con almeno $P$ come bacino. Poichè è anche stabile, per il teorema precedente, è asintoticamente stabile.

 C.D.D.

Esercizio Riprendiamo l'equazione di Lienard:

$$\left\{\begin{array}{lcl} {\displaystyle \dot x} & {\disp... ...y} & {\displaystyle=} &{\displaystyle -x} \end{array}\right.$$

con $f(x)$ dispari e positiva per $x>0$. Si dimostri che l'origine è asintoticamente stabile, e ha per bacino tutto ${\bf R}^2$. (Soluzione)

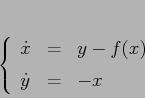
Il teorema di stabilità di Lyapounov consente di trarre delle conclusioni sulla stabilità senza conoscere esplicitamente le soluzioni. D'altro canto non esiste un procedimento automatico valido in tutti i casi per fabbricare le funzioni di Lyapounov, a parte il caso dei pozzi in cui il comportamento qualitativo è già noto. Le funzioni di Lyapounov sono spesso suggerite dall'interpretazione fisica del sistema dinamico, per esempio in termini di energia totale.