Next: 2.4 AUTOVALORI COMPLESSI Up: 2. SISTEMI LINEARI Previous: 2.2 CONVERGENZA Indice Indice analitico
Sommario Il calcolo dell'esponenziale di matrice può essere
eseguito in un diverso sistema di riferimento. Se il nuovo
riferimento è costruito mediante gli autovettori della matrice
data, il calcolo è più semplice; per una matrice
diagonalizzabile (in campo reale) ci si riduce a calcolare
l'esponenziale di una matrice diagonale.
Supponiamo di sottoporre il sistema dinamico lineare
![]() ad un cambiamento di coordinate lineare:
ad un cambiamento di coordinate lineare:
Si suppone che la matrice ![]() sia invertibile,
sia invertibile, ![]() .
Allora l'equazione differenziale si trasforma in questo modo:
.
Allora l'equazione differenziale si trasforma in questo modo:
cioè è ancora un sistema dinamico lineare, la cui matrice
![]() è ottenuta per coniugio da
è ottenuta per coniugio da ![]() . Perciò la
soluzione del sistema trasformato in funzione della
condizione iniziale
. Perciò la
soluzione del sistema trasformato in funzione della
condizione iniziale ![]() sarà espressa mediante
l'esponenziale di matrice:
sarà espressa mediante
l'esponenziale di matrice:
la relazione tra le soluzioni delle due equazioni per ![]() e per
e per ![]() è data da:
è data da:
Per convincersi che la soluzione è la stessa, basta considerare che
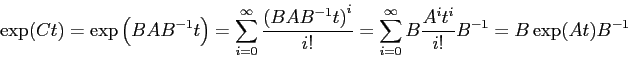
Si noti che le matrici che esprimono i flussi
integrali sono pure coniugate, ed il coniugio è eseguito con la
stessa matrice ![]() del cambiamento di coordinate.
del cambiamento di coordinate.
Si può quindi sempre studiare il sistema dinamico lineare
![]() in un qualunque sistema di riferimento; la matrice
in un qualunque sistema di riferimento; la matrice ![]() si trasforma come la matrice di una trasformazione dello spazio
ambiente
si trasforma come la matrice di una trasformazione dello spazio
ambiente ![]() in sé, cioè per coniugio con la matrice che
esprime il cambiamento di coordinate. Perciò ha senso cercare un
sistema di coordinate in cui la trasformazione definita da
in sé, cioè per coniugio con la matrice che
esprime il cambiamento di coordinate. Perciò ha senso cercare un
sistema di coordinate in cui la trasformazione definita da ![]() abbia
una forma semplice, risolvere il sistema dinamico lineare in quel
sistema di coordinate, e poi ritornare al sistema originale usando
la trasformazione inversa.
abbia
una forma semplice, risolvere il sistema dinamico lineare in quel
sistema di coordinate, e poi ritornare al sistema originale usando
la trasformazione inversa.
Esercizio
Trovare il cambiamento di coordinate lineare che cambia
![\begin{displaymath}
A= \left[\begin{array}{cc}{0}&{1}\\
{1}&{0}\end{array}\ri...
...\left[\begin{array}{cc}{1}&{0}\\
{0}&{-1}\end{array}\right]
\end{displaymath}](img266.png)
Poiché le proprietà geometriche (a meno di trasformazioni
lineari di coordinate) dei sistemi dinamici lineari dipendono solo
dalla classe di equivalenza della matrice ![]() a meno di coniugio,
è logico cercare di utilizzare le quantità che sono
invarianti per coniugio, come gli autovalori; si
utilizzeranno quindi le nozioni di base della
sezione A.1.
a meno di coniugio,
è logico cercare di utilizzare le quantità che sono
invarianti per coniugio, come gli autovalori; si
utilizzeranno quindi le nozioni di base della
sezione A.1.
Definizione:
In questo caso la matrice ![]() è equivalente per coniugio ad una
matrice diagonale:
è equivalente per coniugio ad una
matrice diagonale:
Se gli autovalori sono tutti reali e distinti allora la matrice è diagonalizzabile: gli autovettori di autovalori diversi sono linearmente indipendenti, e quindi costituiscono una base.
Se la matrice ![]() è diagonalizzabile, allora tutte le orbite del
sistema dinamico lineare
è diagonalizzabile, allora tutte le orbite del
sistema dinamico lineare ![]() si possono esprimere mediante
combinazioni lineari di funzioni esponenziali
si possono esprimere mediante
combinazioni lineari di funzioni esponenziali
![]() ,
dove i coefficienti del tempo negli esponenti sono gli autovalori
,
dove i coefficienti del tempo negli esponenti sono gli autovalori
![]() della matrice
della matrice ![]() .
Dimostrazione:
.
Dimostrazione:
In dimensione ![]() dato il sistema dinamico:
dato il sistema dinamico:
![\begin{displaymath}
\left\{\begin{array}{lcl}
{\displaystyle \dot x} & {\displa...
...y}{cc}{a_{11}}&{a_{12}}\\
{a_{21}}&{a_{22}}\end{array}\right]\end{displaymath}](img290.png)
Il numero di soluzioni reali e distinte dell'equazione
caratteristica dipende in questo caso solo dal segno del
discriminante dell'equazione di secondo grado:
Esercizio
![\begin{displaymath}
\dot X =A\, X \hspace{5mm},\hspace{5mm}A=\left[\begin{array}{cc}{1}&{2}\\
{1}&{3}\end{array}\right]
\end{displaymath}](img298.png)
Nel caso ![]() non si può decidere se la matrice è
diagonalizzabile soltanto dal valore di
non si può decidere se la matrice è
diagonalizzabile soltanto dal valore di ![]() ; nei due casi
seguenti:
; nei due casi
seguenti:
![\begin{displaymath}A=\left[\begin{array}{cc}{\lambda_1}&{0}\\
{0}&{\lambda_1}\...
...array}{cc}{\lambda_1}&{1}\\
{0}&{\lambda_1}\end{array}\right]\end{displaymath}](img301.png)
Nel caso ![]() decidere se una matrice è diagonalizzabile, e
diagonalizzarla esplicitamente, può essere tutt'altro che
semplice. Per il teorema fondamentale dell'algebra ogni
matrice
decidere se una matrice è diagonalizzabile, e
diagonalizzarla esplicitamente, può essere tutt'altro che
semplice. Per il teorema fondamentale dell'algebra ogni
matrice ![]() ha
ha ![]() autovalori, reali o complessi, contati
con la loro
molteplicità algebrica.
Però se
autovalori, reali o complessi, contati
con la loro
molteplicità algebrica.
Però se ![]() non esiste alcun algoritmo
esplicito per risolvere l'equazione caratteristica. Le matrici
simmetriche sono sempre diagonalizzabili (vedi
Sezione A.1).
non esiste alcun algoritmo
esplicito per risolvere l'equazione caratteristica. Le matrici
simmetriche sono sempre diagonalizzabili (vedi
Sezione A.1).
Consideriamo il caso di dimensione ![]() ed una matrice
ed una matrice ![]() con
autovalori reali distinti: esistono due autovettori
con
autovalori reali distinti: esistono due autovettori ![]() tali che:
tali che:
![\begin{displaymath}
B\,A\,B^{-1}= \left[\begin{array}{cc}{a}&{0}\\
{0}&{b}\end{array}\right]
\end{displaymath}](img309.png)
Il comportamento qualitativo delle orbite si può studiare nel
sistema in forma canonica, a cui ci si può ricondurre a
meno di trasformazioni lineari:
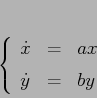
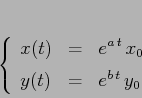
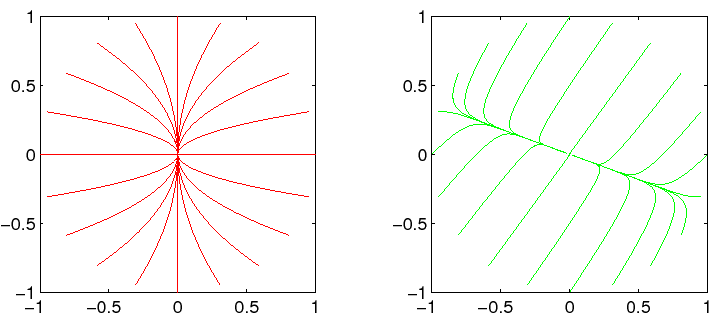
La traiettoria, cioè la curva descritta in ![]() dalle
soluzioni (senza la legge oraria, cioè senza la
parametrizzazione in funzione di
dalle
soluzioni (senza la legge oraria, cioè senza la
parametrizzazione in funzione di ![]() ), si può ricavare (limitandosi
al primo quadrante, le traiettorie relative agli altri tre quadranti
si ottengono per simmetria) elevando la soluzione per
), si può ricavare (limitandosi
al primo quadrante, le traiettorie relative agli altri tre quadranti
si ottengono per simmetria) elevando la soluzione per ![]() alla
potenza
alla
potenza ![]() , e quella per
, e quella per ![]() alla potenza
alla potenza ![]() , e facendo il
quoziente (per
, e facendo il
quoziente (per ![]() ):
):
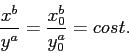
 |
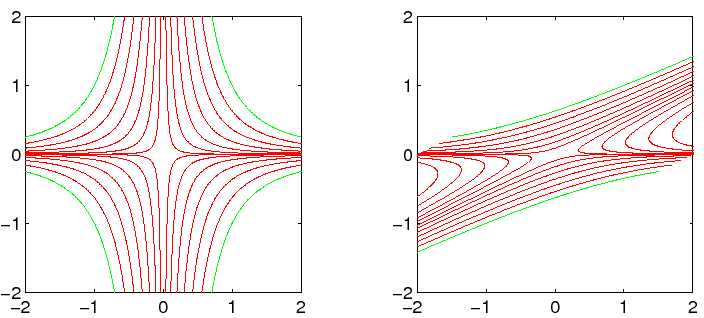 |
Il comportamento qualitativo dipende solo dal segno di ![]() e
e ![]() :
:
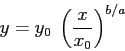
Esercizio
Determinare le orbite del sistema dinamico
![\begin{displaymath}
\dot X=AX\;,\;
A=\left[\begin{array}{cc}{-1}&{4}\\
{-1}&{-6}\end{array}\right]
\end{displaymath}](img334.png)
Andrea Milani 2009-06-01