Next: 2.2 CONVERGENZA Up: 2. SISTEMI LINEARI Previous: 2. SISTEMI LINEARI Indice Indice analitico
Sommario Vogliamo generalizzare la funzione esponenziale in modo che
sia definita per argomenti matrici. Così come la funzione
esponenziale di argomento reale risolve l'equazione differenziale
![]() , l'esponenziale di matrici risolve il più generale
sistema dinamico continuo lineare. Le proprietà dell'esponenziale
di matrici sono strettamente analoghe a quelle della funzione
esponenziale ordinaria, con qualche importante differenza che deriva
dalla non commutatività del prodotto di matrici.
, l'esponenziale di matrici risolve il più generale
sistema dinamico continuo lineare. Le proprietà dell'esponenziale
di matrici sono strettamente analoghe a quelle della funzione
esponenziale ordinaria, con qualche importante differenza che deriva
dalla non commutatività del prodotto di matrici.
Dato il sistema dinamico dell'esempio della
Sezione 1.2: ![]() , con
, con ![]() e
condizione iniziale
e
condizione iniziale ![]() , si può porre il problema in forma
integrale:
, si può porre il problema in forma
integrale:
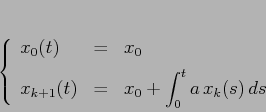
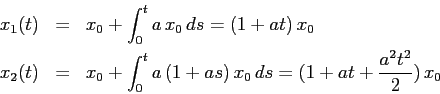
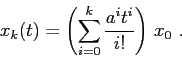
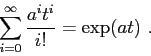
Consideriamo ora il caso generale di un
sistema dinamico continuo lineare
![]() con condizione iniziale
con condizione iniziale ![]() con
con
![]() ,
, ![]() di tipo
di tipo ![]() . La forma integrale sarà:
. La forma integrale sarà:
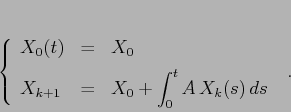
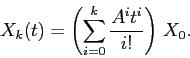
Si noti che tutti questi passaggi sono del tutto identici a quelli del
caso scalare, a parte la sostituzione delle lettere minuscole con le
maiuscole. Questo è possibile perché in nessuno di questi passaggi
si è usata la proprietà commutativa della moltiplicazione, che non
vale per il prodotto di matrici (e non ha neppure senso per il
prodotto di matrici con vettori). Per ottenere questo risultato
bisogna però tenere ![]() , come
, come ![]() , a destra nelle formule.
, a destra nelle formule.
Perciò la soluzione sarà in qualche modo rappresentata dalla serie
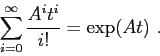
La formula qui sopra può essere usata come definizione della funzione
esponenziale di matrice:
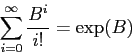
![\begin{displaymath}
A=\left[\begin{array}{cc}{0}&{0}\\
{1}&{0}\end{array}\right]\end{displaymath}](img217.png)
![\begin{displaymath}
\exp(At)=I + At=\left[\begin{array}{cc}{1}&{0}\\
{t}&{1}\end{array}\right].\end{displaymath}](img219.png)
Questi esempi sono abbastanza generali, nel senso che ci si
può ricondurre a questi, o ad una combinazione di questi, per
calcolare le esponenziali di matrice in tutti i casi in cui la
matrice ![]() ha autovalori reali; e quindi per risolvere molti
sistemi dinamici continui lineari. Questo procedimento di riduzione
a casi più semplici sarà presentato nelle
Sezioni 2.3, 2.5.
ha autovalori reali; e quindi per risolvere molti
sistemi dinamici continui lineari. Questo procedimento di riduzione
a casi più semplici sarà presentato nelle
Sezioni 2.3, 2.5.
Esercizio
Scrivere le soluzioni del sistema dinamico continuo lineare
![]() nei seguenti casi:
nei seguenti casi:
![\begin{displaymath}
A=\left[\begin{array}{cc}{0}&{1}\\
{1}&{0}\end{array}\rig...
...ay}{ccc}
0 & 0 & 0\\ 1 & 0 & 0\\ 0 & 1 & 0\end{array}\right]
\end{displaymath}](img223.png)
Suggerimento: per la prima matrice usare le serie di Taylor
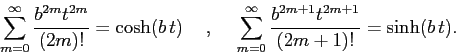
Andrea Milani 2009-06-01