Next: A.5 EQUAZIONI DIFFERENZIALI Up: A. REQUISITI DI ALGEBRA, Previous: A.3 TOPOLOGIA Indice Indice analitico
Definizione:
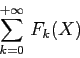
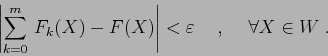
Una serie di potenze è una serie di funzioni ciascuna
rappresentata da un monomio: per esempio in una sola variabile ![]()
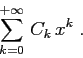
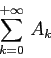
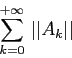
Questo teorema in sostanza equivale all'affermazione che lo
spazio ![]() (o
(o ![]() ) è uno spazio metrico completo.
) è uno spazio metrico completo.
All'interno del raggio di convergenza, la serie converge ad una
funzione ![]() derivabile, e la derivata è la somma della serie
ottenuta derivando termine a termine
derivabile, e la derivata è la somma della serie
ottenuta derivando termine a termine
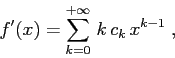
che ha lo stesso raggio di convergenza.
Date due serie di potenze, se esse sono convergenti e convergenti in norma:
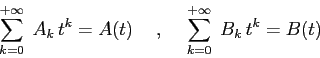
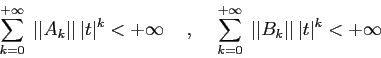
allora la loro serie prodotto secondo Cauchy è convergente
in norma, e converge alla funzione prodotto ![]() .
.
Una serie uniformemente convergente di funzioni continue ha per limite una funzione continua.
Bibliografia :
Andrea Milani 2009-06-01