Next: 2.3 AUTOVALORI REALI Up: 2. SISTEMI LINEARI Previous: 2.1 ESPONENZIALE DI MATRICI Indice Indice analitico
Sommario Elenchiamo le proprietà più utili dell'esponenziale di
matrici, a partire dalla sua convergenza. Le dimostrazioni di questi
teoremi seguono dalla teoria della convergenza uniforme delle serie di
funzioni, utilizzando la diseguaglianza di Cauchy. Le proprietà della
funzione esponenziale sono conservate dall'esponenziale di matrici
purché non dipendano dalla proprietà commutativa della
moltiplicazione: in particolare l'esponenziale della somma è uguale
al prodotto delle esponenziali solo se il prodotto commuta.
La convergenza dell'esponenziale di matrice può essere dimostrata come conseguenza della convergenza in norma della serie.
Sia ![]() una qualsiasi matrice quadrata
una qualsiasi matrice quadrata ![]() . Allora la serie
esponenziale:
. Allora la serie
esponenziale:
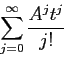
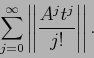
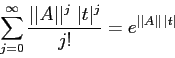
Questo teorema basta a dimostrare l'esistenza del flusso
integrale di un qualsiasi sistema dinamico continuo lineare
![]() , che è la somma della serie convergente
, che è la somma della serie convergente
![]() . Però calcolare esplicitamente tale soluzione non è
immediato. Il procedimento di calcolo sarà spiegato nelle
Sezioni 2.3, 2.4,
2.5.
. Però calcolare esplicitamente tale soluzione non è
immediato. Il procedimento di calcolo sarà spiegato nelle
Sezioni 2.3, 2.4,
2.5.
Consideriamo due serie di matrici convergenti, della forma:
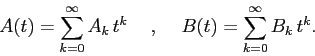
La dipendenza dalla variabile ![]() non è veramente essenziale
in questo ragionamento, che può essere svolto sostituendo
non è veramente essenziale
in questo ragionamento, che può essere svolto sostituendo ![]() ; ma
come vedremo questa semplificazione renderebbe meno comprensibile il
procedimento.
; ma
come vedremo questa semplificazione renderebbe meno comprensibile il
procedimento.
Definizione:
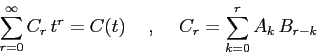
Le condizioni di convergenza della serie, ad una funzione continua
![]() , sono descritte dal teorema del prodotto secondo Cauchy.
Per l'applicazione che ci interessa, basta sapere che se le
due serie per
, sono descritte dal teorema del prodotto secondo Cauchy.
Per l'applicazione che ci interessa, basta sapere che se le
due serie per ![]() convergono in norma per ogni
convergono in norma per ogni ![]() ,
allora la serie prodotto converge in norma, quindi anche converge per
ogni
,
allora la serie prodotto converge in norma, quindi anche converge per
ogni ![]() , e la sua somma
, e la sua somma
![]() .
.
Se due matrici quadrate ![]() ,
, ![]() e
e ![]() , commutano tra
loro, cioè
, commutano tra
loro, cioè ![]() , allora l'esponenziale della somma è il
prodotto delle esponenziali:
, allora l'esponenziale della somma è il
prodotto delle esponenziali:
Dimostrazione:
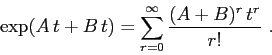
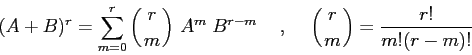
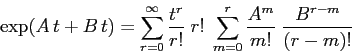
![\begin{displaymath}
\exp(A\,t + B\, t)= \left[\sum_{j=0}^\infty \frac{A^j\, t^j...
...0}^\infty \frac{B^m\, t^m}{m!}\right]= \exp(A\,t)\,\exp(B\,t)
\end{displaymath}](img248.png)
La funzione a valori matriciali ![]() è derivabile, e la
sua derivata è:
è derivabile, e la
sua derivata è:
Resta da verificare che ![]() commuta con
commuta con ![]() ; in effetti
; in effetti ![]() commuta con
commuta con ![]() , quindi anche con ogni addendo della serie
esponenziale, e poiché la moltiplicazione di matrici è
un'operazione continua, la relazione di commutazione passa al
limite.
, quindi anche con ogni addendo della serie
esponenziale, e poiché la moltiplicazione di matrici è
un'operazione continua, la relazione di commutazione passa al
limite.
Andrea Milani 2009-06-01