Next: 6. CAOS Up: 5. SISTEMI CONSERVATIVI Previous: 5.5 TRASFORMAZIONI CANONICHE Indice Indice analitico
Sommario Se un aperto del piano delle fasi è riempito da orbite
periodiche, si vorrebbe parametrizzare ciascuna di queste con una
variabile angolo, che si accresca di ![]() in un periodo. Se la
variabile angolo così ottenuta fa parte di una coppia di
coordinate canoniche, queste ultime possono ridurre il problema ad uno
banale in cui il flusso integrale è formato da soli scorrimenti.
in un periodo. Se la
variabile angolo così ottenuta fa parte di una coppia di
coordinate canoniche, queste ultime possono ridurre il problema ad uno
banale in cui il flusso integrale è formato da soli scorrimenti.
Se la hamiltoniana ![]() sull'aperto
sull'aperto
![]() ha insiemi di livello tutti compatti, che si riducono ad una sola
curva regolare, semplice e chiusa, allora ognuna di queste curve di
livello individua un'orbita periodica. Bisogna in effetti
distinguere due casi: se la coordinata
ha insiemi di livello tutti compatti, che si riducono ad una sola
curva regolare, semplice e chiusa, allora ognuna di queste curve di
livello individua un'orbita periodica. Bisogna in effetti
distinguere due casi: se la coordinata ![]() appartiene a
appartiene a ![]() , allora
un'orbita periodica deve avere entrambe le funzioni
, allora
un'orbita periodica deve avere entrambe le funzioni ![]() periodiche con lo stesso periodo
periodiche con lo stesso periodo ![]() :
:
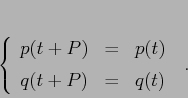
In questo caso si parla di orbite periodiche del tipo librazione.
La curva di livello racchiude una parte del piano in cui (se ![]() è definita) deve esserci almeno un punto di equilibrio. In questo
caso le curve di livello corrispondenti a valori vicini riempiono un
insieme diffeomorfo ad una corona circolare.
è definita) deve esserci almeno un punto di equilibrio. In questo
caso le curve di livello corrispondenti a valori vicini riempiono un
insieme diffeomorfo ad una corona circolare.
Se invece la coordinata ![]() è una variabile angolo, lo
spazio delle fasi è in effetti contenuto in un cilindro
è una variabile angolo, lo
spazio delle fasi è in effetti contenuto in un cilindro
![]() , e un'orbita periodica può essere di due tipi: di
librazione (in cui entrambe le coordinate sono funzioni periodiche di periodo
, e un'orbita periodica può essere di due tipi: di
librazione (in cui entrambe le coordinate sono funzioni periodiche di periodo
![]() ), e di circolazione con
), e di circolazione con
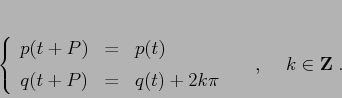
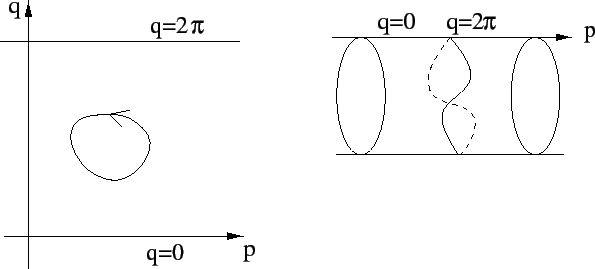 |
Esempio:
Se il livello di energia ![]() è tale che
è tale che ![]() , allora
, allora
Se al contrario ![]() (incluso il caso
(incluso il caso ![]() illimitata),
allora ci sono dei valori per l'angolo
illimitata),
allora ci sono dei valori per l'angolo ![]() in cui
in cui ![]() :
questi valori sono ``proibiti'' per l'insieme di livello
:
questi valori sono ``proibiti'' per l'insieme di livello ![]() ; se
; se
![]() ha un minimo, l'insieme di livello è compatto, e se non
contiene punti di equilibrio si ottiene un'orbita periodica del tipo
della librazione.
ha un minimo, l'insieme di livello è compatto, e se non
contiene punti di equilibrio si ottiene un'orbita periodica del tipo
della librazione.
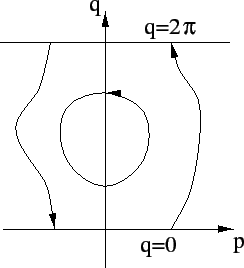 |
Problema
Dimostrare che nelle orbite periodiche del tipo della circolazione
![]() , cioè l'orbita non può richiudersi dopo più di un giro.
, cioè l'orbita non può richiudersi dopo più di un giro.
Suggerimento: Considerare la curva ![]() sull'intervallo
sull'intervallo ![]() , dove
, dove ![]() è il periodo. Se quando
è il periodo. Se quando ![]() è cresciuto di
è cresciuto di
![]() il valore di
il valore di ![]() fosse diverso...
fosse diverso...
Si noti che l'affermazione del problema precedente non vale per un sistema discreto: in una mappa standard del pendolo ci sono punti periodici di qualsiasi periodo, e che fanno fare ad una variabile angolo un numero arbitrario di giri.
Per descrivere un simile pacchetto di orbite periodiche l'ideale
sarebbe disporre di un sistema di coordinate ![]() tale che un aperto
tale che un aperto ![]() del piano delle fasi, costituito solo da orbite periodiche (tutte del
tipo librazione o tutte del tipo circolazione), sia mandato
nel rettangolo
del piano delle fasi, costituito solo da orbite periodiche (tutte del
tipo librazione o tutte del tipo circolazione), sia mandato
nel rettangolo
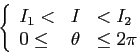
In un tale sistema di coordinate, il sistema hamiltoniano è risolto
banalmente, con il flusso integrale in funzione della condizione
iniziale
![]() dato da soli scorrimenti:
dato da soli scorrimenti:
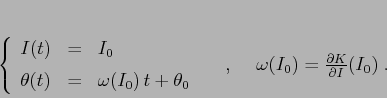
![]() è una velocità angolare, quindi ha la
dimensione dell'inverso del tempo; se supponiamo che la
hamiltoniana sia dimensionalmente un'energia, allora la variabile
è una velocità angolare, quindi ha la
dimensione dell'inverso del tempo; se supponiamo che la
hamiltoniana sia dimensionalmente un'energia, allora la variabile ![]() ha la dimensione di un'energia moltiplicata per un tempo, e per questo
si chiama variabile azione. La
frequenza
ha la dimensione di un'energia moltiplicata per un tempo, e per questo
si chiama variabile azione. La
frequenza ![]() , che è costante per ogni orbita, si chiama
frequenza propria.
, che è costante per ogni orbita, si chiama
frequenza propria.
Esempio:
con ![]() una lunghezza caratteristica del corpo ed
una lunghezza caratteristica del corpo ed ![]() un
coefficiente che dipende dalla forma e distribuzione di massa (per
esempio
un
coefficiente che dipende dalla forma e distribuzione di massa (per
esempio ![]() per una sfera di densità uniforme, essendo
per una sfera di densità uniforme, essendo ![]() il raggio); il potenziale è
il raggio); il potenziale è ![]() , quindi dalla trasformata di
Legendre:
, quindi dalla trasformata di
Legendre:
Poiché la hamiltoniana è funzione solo di ![]() ,
, ![]() è una
coppia di variabili azione-angolo. Si noti che
è una
coppia di variabili azione-angolo. Si noti che ![]() cambia con
velocità angolare
cambia con
velocità angolare
![]() , quindi
, quindi ![]() è il
momento angolare, che ha la dimensione di un azione.
è il
momento angolare, che ha la dimensione di un azione.
Esempio:
la trasformazione canonica
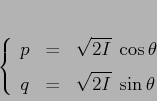
semplifica il sistema riducendo la hamiltoniana a
da cui ![]() è una variabile azione,
è una variabile azione, ![]() una variabile angolo,
con frequenza propria
una variabile angolo,
con frequenza propria ![]() costante rispetto ad
costante rispetto ad ![]() .
.
Esercizio
Trovare le variabili azione ed angolo per la funzione di Hamilton
che esprime l'oscillatore armonico più generale. (Soluzione)
Abbiamo visto i vantaggi che presenterebbe la disponibilità di una coppia di variabili canoniche delle quali la prima sia una variabile azione e la seconda una variabile angolo, tali che la hamiltoniana trasformata sia funzione della sola azione; in questo caso parliamo di variabili azione-angolo.
Data una hamiltoniana ![]() , per trovare una adeguata variabile
azione si può impiegare la proprietà delle trasformazioni canoniche
di conservare l'area. Supponiamo che
, per trovare una adeguata variabile
azione si può impiegare la proprietà delle trasformazioni canoniche
di conservare l'area. Supponiamo che ![]() sia una orbita
periodica (di periodo
sia una orbita
periodica (di periodo ![]() ) del tipo librazione; allora la traiettoria
è una curva nel piano
) del tipo librazione; allora la traiettoria
è una curva nel piano ![]() che fa da bordo
che fa da bordo ![]() ad un
insieme
ad un
insieme ![]() , la cui area può essere calcolata con la
formula di Green:
, la cui area può essere calcolata con la
formula di Green:
L'insieme ![]() viene trasformato nel piano
viene trasformato nel piano ![]() in un insieme che
chiamiamo
in un insieme che
chiamiamo ![]() , la cui area è, per la stessa formula:
, la cui area è, per la stessa formula:
Ora la curva ![]() nel piano
nel piano ![]() altro non è che la
soluzione corrispondente a
altro non è che la
soluzione corrispondente a ![]() nel piano
nel piano ![]() ; se imponiamo
la condizione che
; se imponiamo
la condizione che ![]() siano variabili azione-angolo, allora
siano variabili azione-angolo, allora ![]() è
costante e
è
costante e ![]() varia in
varia in ![]() , quindi (Figura 5.13)
, quindi (Figura 5.13)
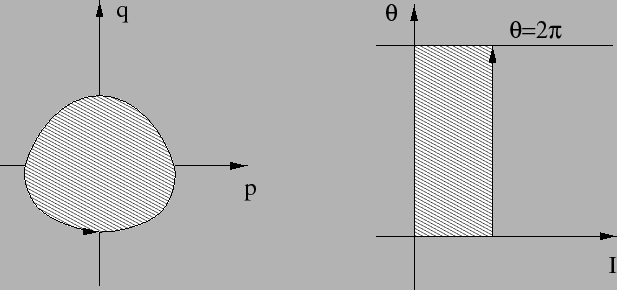 |
ossia, la variabile azione è l'area racchiusa dall'orbita periodica,
divisa per ![]() .
.
In realtà la variabile azione è definita a meno di una
costante, ma noi abbiamo imposto che
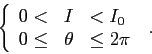
Per esempio, se le orbite periodiche di ![]() sono quelle che attorniano
un punto di equilibrio stabile, abbiamo imposto che
sono quelle che attorniano
un punto di equilibrio stabile, abbiamo imposto che ![]() tenda a zero
quando l'orbita periodica tende al punto di equilibrio. Se le orbite
periodiche per cui si sta cercando la variabile azione racchiudono
più di un punto di equilibrio, allora la variabile azione è
inevitabilmente definita a meno di una costante arbitraria; lo stesso
vale per le orbite periodiche di tipo circolazione.
tenda a zero
quando l'orbita periodica tende al punto di equilibrio. Se le orbite
periodiche per cui si sta cercando la variabile azione racchiudono
più di un punto di equilibrio, allora la variabile azione è
inevitabilmente definita a meno di una costante arbitraria; lo stesso
vale per le orbite periodiche di tipo circolazione.
Se la hamiltoniana è del tipo
La soluzione è quindi ottenuta invertendo la funzione ![]() .
Se questo è possibile si ottiene
.
Se questo è possibile si ottiene ![]() , la cui derivata è la
frequenza
, la cui derivata è la
frequenza ![]() che fornisce il periodo
che fornisce il periodo
![]() .
.
Problema
Dimostrare che ogni orbita periodica di una hamiltoniana del tipo
![]() passa da esattamente due punti con
passa da esattamente due punti con ![]() .
.
Suggerimento: All'interno della curva deve esserci un punto di
equilibrio, che può stare solo su ![]() , perciò ci sono almeno
due intersezioni con
, perciò ci sono almeno
due intersezioni con ![]() .
.
Esercizio
Consideriamo la hamiltoniana del pendolo
Problema
Trovare la variabile azione per una palla ``perfettamente elastica''
di massa ![]() che rimbalza tra due muri fissi a distanza
che rimbalza tra due muri fissi a distanza ![]() tra di
loro. Questo problema contiene un muro di potenziale duro,
in cui il potenziale salta da
tra di
loro. Questo problema contiene un muro di potenziale duro,
in cui il potenziale salta da ![]() per
per ![]() a
a
![]() per
per ![]() .
.
Suggerimento: Le soluzioni generalizzate sono segmenti con momento ![]() ,
quindi velocità
,
quindi velocità ![]() , costante nel tratto tra
, costante nel tratto tra ![]() e
e ![]() ,
poi il momento cambia segno istantaneamente.
,
poi il momento cambia segno istantaneamente.
Cerchiamo di descrivere la trasformazione canonica a variabili azione-angolo
con una funzione generatrice
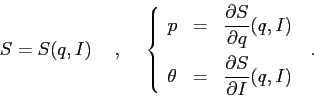
Una soluzione nel piano ![]() descrive una curva di livello
descrive una curva di livello ![]() ;
nel piano
;
nel piano ![]() la soluzione corrispondente ha equazione
la soluzione corrispondente ha equazione ![]() ,
quindi
,
quindi ![]() costante. Se ci restringiamo ad una singola orbita periodica
con azione
costante. Se ci restringiamo ad una singola orbita periodica
con azione ![]() , la derivata parziale di
, la derivata parziale di ![]() rispetto a
rispetto a ![]() è la funzione
di
è la funzione
di ![]() che fornisce
che fornisce ![]() , quindi
, quindi
non è mai nullo, e quindi la funzione ![]() è una
funzione polidroma, soltanto localmente definita
in modo univoco; ad ogni giro la funzione aumenta di una quantità fissa
è una
funzione polidroma, soltanto localmente definita
in modo univoco; ad ogni giro la funzione aumenta di una quantità fissa
![]() . Del resto
la variabile angolo
. Del resto
la variabile angolo ![]() può essere calcolata come
può essere calcolata come
e il suo incremento dopo un giro sull'orbita periodica è
Le funzioni generatrici si ottengono come funzioni potenziali di forme chiuse, quindi localmente esatte, ma non necessariamente esatte in grande: ciò significa appunto che non sono necessariamente funzioni ad un solo valore. Questo però non impedisce che la trasformazione canonica sia ben definita, in particolare quando si vuole ottenere una variabile angolo.
Esempio:
![\begin{displaymath}
I(E)= \frac 1{\pi} \;\int_{q_1}^{q_2}\sqrt{2m[E-V(q)]}\; dq...
... \;\int_{q_1}^{q_2}
\;\sqrt{1-\frac{m\omega^2}{2E}\,q^2}\;dq
\end{displaymath}](img2077.png)
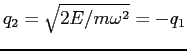 . Questo integrale è elementare, con
la sostituzione
. Questo integrale è elementare, con
la sostituzione
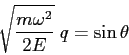
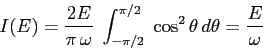
La variabile usata nella sostituzione in effetti è la variabile angolo.
A questo punto
![]() e la frequenza
e la frequenza ![]() , come
sappiamo, è costante. Se si calcola la funzione generatrice
a partire dalla esplicitazione di
, come
sappiamo, è costante. Se si calcola la funzione generatrice
a partire dalla esplicitazione di ![]() :
:
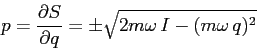
![\begin{eqnarray*}
S(q,I)&=& \sqrt{2m\omega\,I} \int_0^{q}
\sqrt{1-\frac{m\omeg...
...eta
= I\left[ \theta + \sin\theta\,\cos\theta \right]_0^\theta
\end{eqnarray*}](img2086.png)
![\begin{displaymath}
S(q,I)= I\,\arcsin\left[\sqrt{\frac{m\omega}{2I}}\,q \right]
+q \,\sqrt{\frac{m\omega\,I}2-\frac{m^2\omega^2\,q^2}4}\;.
\end{displaymath}](img2088.png)
Si noti che il primo termine altro non è che ![]() .
.
Questo esempio, che pure è il più semplice possibile di un calcolo esplicito delle variabili azione angolo mediante quadrature, è già abbastanza difficile. In effetti le variabili azione-angolo sono soprattutto utili come strumento di descrizione geometrica, non necessariamente di calcolo esplicito. Per una trattazione delle variabili angolo, sempre nel contesto dei sistemi ad un grado di libertà, si veda [Percival-Richards 82], ai Capitoli 8 e 9, e [Goldstein 1950], Capitolo 9.
Andrea Milani 2009-06-01