Next: 5.6 VARIABILI AZIONE ANGOLO Up: 5. SISTEMI CONSERVATIVI Previous: 5.4 SISTEMI LAGRANGIANI Indice Indice analitico
Sommario La funzione hamiltoniana è un modo conveniente di
descrivere un sistema dinamico conservativo; tuttavia le equazioni di
Hamilton dipendono dalla scelta di un sistema di coordinate, e non
sono invarianti rispetto ad un cambiamento di coordinate nel piano
![]() . Le trasformazioni canoniche sono quei cambiamenti di coordinate
che consentono di conservare la descrizione del sistema dinamico
mediante la funzione hamiltoniana, anzi mediante la stessa funzione di
Hamilton, espressa nel nuovo sistema. Le trasformazioni canoniche possono
a loro volta essere descritte in termini di una sola funzione
generatrice, che però in molti casi significativi risulta una
``funzione a più valori''.
. Le trasformazioni canoniche sono quei cambiamenti di coordinate
che consentono di conservare la descrizione del sistema dinamico
mediante la funzione hamiltoniana, anzi mediante la stessa funzione di
Hamilton, espressa nel nuovo sistema. Le trasformazioni canoniche possono
a loro volta essere descritte in termini di una sola funzione
generatrice, che però in molti casi significativi risulta una
``funzione a più valori''.
Vogliamo determinare quali cambiamenti di coordinate
trasformano le equazioni di Hamilton
con hamiltoniana ![]() nelle
equazioni di Hamilton con hamiltoniana
nelle
equazioni di Hamilton con hamiltoniana ![]() . Il problema diventa
più facile se si impone la condizione - più restrittiva- che le
due hamiltoniane siano ottenute mediante la stessa trasformazione, come
le funzioni con gli stessi valori nei punti corrispondenti:
. Il problema diventa
più facile se si impone la condizione - più restrittiva- che le
due hamiltoniane siano ottenute mediante la stessa trasformazione, come
le funzioni con gli stessi valori nei punti corrispondenti:
Se per ogni hamiltoniana ![]() (di classe
(di classe ![]() ), il cambiamento di
coordinate
), il cambiamento di
coordinate ![]() preserva la forma hamiltoniana della dinamica, con
hamiltoniane che si corrispondono per valore,
preserva la forma hamiltoniana della dinamica, con
hamiltoniane che si corrispondono per valore, ![]() si dice
trasformazione canonica.
si dice
trasformazione canonica.
Sia ![]() un cambiamento di coordinate che sia un diffeomorfismo
(
un cambiamento di coordinate che sia un diffeomorfismo
(![]() e con inversa
e con inversa ![]() ); se
); se ![]() è la matrice jacobiana di
è la matrice jacobiana di
![]() :
:
![\begin{displaymath}
A=\frac{\partial {(w,z)}}{\partial {(p,q)}} = \left[\begin{...
...l {p}}}&{\frac{\partial {z}}{\partial {q}}}\end{array}\right]
\end{displaymath}](img1887.png)
Dimostrazione:
![\begin{displaymath}
\frac d{d\,t}\left[\begin{array}{c}{p}\\
{q}\end{array}\r...
...{array}{c}{w}\\
{z}\end{array}\right] = J\,\nabla K(w,z)\;.
\end{displaymath}](img1890.png)
Calcoliamo la velocità nel piano ![]() considerando le coordinate
considerando le coordinate ![]() come funzione delle
come funzione delle ![]() :
:
![\begin{displaymath}
\frac d{d\,t}\left[\begin{array}{c}{w(p,q)}\\
{z(p,q)}\en...
...\left[\begin{array}{c}{\dot p}\\
{\dot q}\end{array}\right]
\end{displaymath}](img1891.png)
![\begin{displaymath}
\frac d{d\,t}\left[\begin{array}{c}{w(p,q)}\\
{z(p,q)}\end{array}\right]= A\, J \, \nabla H(p,q)\;.
\end{displaymath}](img1892.png)
Ora si tratta di stabilire quale relazione esista tra il gradiente
![]() e quello
e quello ![]() ; se facciamo l'ipotesi che le due
funzioni si
corrispondano per valore,
utilizzando il differenziale della funzione composta si ottiene
; se facciamo l'ipotesi che le due
funzioni si
corrispondano per valore,
utilizzando il differenziale della funzione composta si ottiene
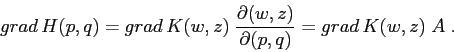
Per sostituire nell'equazione precedente occorre tenere presente che
![]()
![\begin{displaymath}
\frac d{d\,t}\left[\begin{array}{c}{w(p,q)}\\
{z(p,q)}\end{array}\right]= A\, J \, A^T\, \nabla K(w(p,q),z(p,q))\;.
\end{displaymath}](img1898.png)
Allora i due sistemi di equazioni di Hamilton si
corrispondono in ogni punto se e solo se vale identicamente:
Eseguendo il calcolo dei prodotti di matrici:
![\begin{displaymath}
A=\left[\begin{array}{cc}{a}&{b}\\
{c}&{d}\end{array}\right]\hspace{5mm},\hspace{5mm}A\,J\,A^T=
\end{displaymath}](img1900.png)
![\begin{displaymath}
= \left[\begin{array}{cc}{a}&{b}\\
{c}&{d}\end{array}\rig...
...b}&{bc-ad}\\
{da-cb}&{dc-cd}\end{array}\right]= (ad-bc)\, J
\end{displaymath}](img1901.png)
Un'altro modo di presentare lo stesso risultato usando le
parentesi di Poisson è il seguente: la trasformazione
![]() è canonica se e solo se
è canonica se e solo se
Abbiamo già visto che il flusso integrale di un sistema
hamiltoniano è conservativo, cioè conserva l'area. In effetti è
intuitivo che il flusso integrale per un tempo ![]() fisso è
un'equivalenza tra le dinamiche,
se le equazioni differenziali non dipendono dal tempo; quindi il
flusso integrale
fisso è
un'equivalenza tra le dinamiche,
se le equazioni differenziali non dipendono dal tempo; quindi il
flusso integrale ![]() è una trasformazione canonica per ogni
è una trasformazione canonica per ogni ![]() per cui è definito.
per cui è definito.
Esempio:
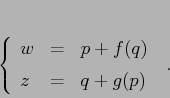
![\begin{displaymath}
A=\frac{\partial {(w,z)}}{\partial {(p,q)}}=\left[\begin{array}{cc}{1}&{f'(q)}\\
{g'(p)}&{1}\end{array}\right]
\end{displaymath}](img1908.png)
Esempio:
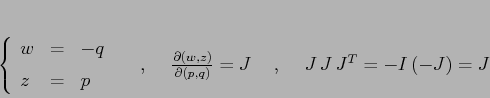
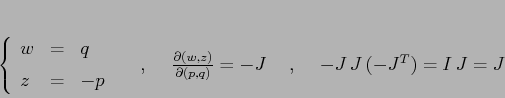
![\begin{displaymath}
\frac{\partial {(p,q)}}{\partial {(I,\theta)}} = \left[\beg...
...'(I)\sin\theta}&{\phantom{-}f(I)\cos\theta}\end{array}\right]
\end{displaymath}](img1917.png)
Esercizio
Data la trasformazione della coordinata ![]() definita da
definita da ![]() , dove
, dove
![]() è una funzione
è una funzione ![]() con
con ![]() , trovare tutte le
possibili trasformazioni canonica
, trovare tutte le
possibili trasformazioni canonica
![]() per cui la
seconda coordinata è espressa da
per cui la
seconda coordinata è espressa da ![]() .
(Soluzione)
.
(Soluzione)
Problema
Trovare tutte le trasformazioni canoniche lineari:
![\begin{displaymath}
\left[\begin{array}{c}{w}\\
{z}\end{array}\right]=A \, \left[\begin{array}{c}{p}\\
{q}\end{array}\right]\;,
\end{displaymath}](img1925.png)
Suggerimento: Questo problema è già stato menzionato al momento della definizione di sistema dinamico discreto conservativo.
Usando l'equazione caratteristica
![]() ,
in cui l'unico coefficiente variabile è la traccia, si
trova il criterio della traccia per cui
,
in cui l'unico coefficiente variabile è la traccia, si
trova il criterio della traccia per cui ![]() caratterizza le matrici simplettiche stabili che sono
rotazioni,
caratterizza le matrici simplettiche stabili che sono
rotazioni, ![]() caratterizza le
matrici simplettiche iperboliche
con autovalori reali
caratterizza le
matrici simplettiche iperboliche
con autovalori reali
![]() ; per
; per
![]() ci sono due casi, a seconda se la matrice è o no
diagonalizzabile.
ci sono due casi, a seconda se la matrice è o no
diagonalizzabile.
Abbiamo visto come verificare che una data trasformazione è canonica, usando il determinante jacobiano. Cerchiamo un metodo per costruire trasformazioni canoniche: per questo si sfrutta l'equivalenza della proprietà di essere canonica con la proprietà di conservare l'area.
L'area di un insieme limitato e chiuso ![]() nel piano delle variabili
nel piano delle variabili ![]() si misura mediante l'integrale doppio
si misura mediante l'integrale doppio
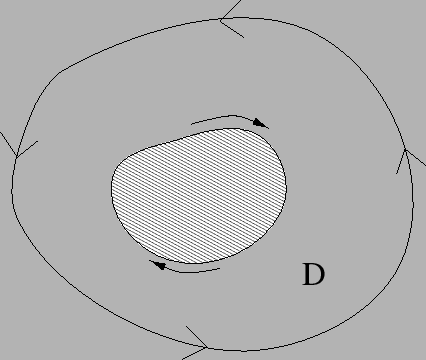
Anche nel caso di insiemi di forma più complessa il cui bordo
è diviso in componenti connesse, ciascuna delle quali è una curva
chiusa, vale la formula di Green purché si intenda che ogni curva
del bordo sia percorsa in modo da lasciarsi l'insieme ![]() a sinistra
rispetto alla velocità sulla curva. Nell'esempio della
Figura 5.10 si vede un insieme
a sinistra
rispetto alla velocità sulla curva. Nell'esempio della
Figura 5.10 si vede un insieme ![]() che non è
semplicemente connesso, il cui bordo consiste di due curve,
percorse in senso antiorario per il bordo esterno ed orario per il
bordo interno.
che non è
semplicemente connesso, il cui bordo consiste di due curve,
percorse in senso antiorario per il bordo esterno ed orario per il
bordo interno.
L'espressione ![]() è una forma differenziale lineare,
dove la ``funzione coordinata''
è una forma differenziale lineare,
dove la ``funzione coordinata'' ![]() è una funzione del punto sulla curva.
è una funzione del punto sulla curva.
Consideriamo ora una trasformazione
![]() , definita (e
di classe
, definita (e
di classe ![]() ) su di un aperto
) su di un aperto
![]() ; l'immagine di
; l'immagine di
![]() per la trasformazione sia
per la trasformazione sia ![]() . L'ipotesi che la
trasformazione sia canonica si traduce nell'eguaglianza delle aree:
. L'ipotesi che la
trasformazione sia canonica si traduce nell'eguaglianza delle aree:
Applicando la formula di Green nel piano ![]() , nella forma
con la prima coordinata come variabile di integrazione:
, nella forma
con la prima coordinata come variabile di integrazione:
Per la continuità della trasformazione, la curva (o le curve) che
costituisce il bordo ![]() è l'immagine mediante la
trasformazione della curva (o curve) che costituisce il bordo
è l'immagine mediante la
trasformazione della curva (o curve) che costituisce il bordo
![]() . Perciò si può interpretare l'integrale di linea su
. Perciò si può interpretare l'integrale di linea su
![]() come integrale su
come integrale su ![]() della forma differenziale
della forma differenziale
![]() .
.
I cambiamenti di coordinate possono sempre essere interpretati
come applicazioni tra due insiemi distinti oppure come
parametrizzazione, con coppie di numeri diversi, dei punti dello
stesso insieme. Il ragionamento che precede usa il secondo modo di
pensare.
 |
Allora l'eguaglianza delle aree si traduce nell'annullarsi di
un'espressione calcolata nelle sole variabili ``vecchie'', cioè
![]() :
:
Sia ![]() un insieme aperto del piano
un insieme aperto del piano ![]() , e sia
, e sia
Sia ![]() un punto di
un punto di ![]() tale che
tale che
![]() . Allora esiste un intorno
. Allora esiste un intorno ![]() di
di ![]() su
cui la
su
cui la ![]() può essere descritta come segue: esiste una funzione
può essere descritta come segue: esiste una funzione
![]() , di classe
, di classe ![]() , delle variabili
, delle variabili ![]() , detta
funzione generatrice, il cui
differenziale è:
, detta
funzione generatrice, il cui
differenziale è:
Viceversa, se esiste in un intorno di ![]() una funzione
una funzione ![]()
![]() che soddisfa la condizione (5.2), allora essa
definisce implicitamente tramite le equazioni (5.1) una
trasformazione canonica da un intorno di
che soddisfa la condizione (5.2), allora essa
definisce implicitamente tramite le equazioni (5.1) una
trasformazione canonica da un intorno di
![]() a un intorno di
a un intorno di
![]() .
.
Dimostrazione:
![\begin{displaymath}
(q,w)\;\longmapsto \; (w,z)\hspace{5mm},\hspace{5mm}
\frac...
...tial z/\partial q}&{\partial
z/\partial w}\end{array}\right]
\end{displaymath}](img1959.png)
Allora possiamo considerare la forma differenziale
![]() . Poiché essa proviene, per cambiamento di variabili,
dalla forma differenziale chiusa
. Poiché essa proviene, per cambiamento di variabili,
dalla forma differenziale chiusa
![]() , e la
proprietà di essere chiusa non dipende dal sistema di coordinate
(si veda Appendice A.2), anche
, e la
proprietà di essere chiusa non dipende dal sistema di coordinate
(si veda Appendice A.2), anche
![]() è una forma chiusa, e quindi localmente una
forma esatta, in un intorno
è una forma chiusa, e quindi localmente una
forma esatta, in un intorno ![]() di
di ![]() :
:
Ossia, in termini di derivate parziali, il campo vettoriale
![]() è il campo gradiente di una funzione
è il campo gradiente di una funzione ![]() ,
di classe
,
di classe ![]() in un intorno di
in un intorno di ![]() , dove
, dove ![]() è
definito da
è
definito da
![]() .
Valgono perciò le equazioni
.
Valgono perciò le equazioni
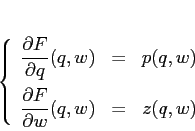
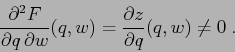
Esempio:
Esercizio
Data la trasformazione di coordinate
La funzione generatrice è una funzione di variabili
``miste'', cioè una ``vecchia'' ed una ``nuova''. Però
la scelta di ![]() nella coppia
nella coppia ![]() e di
e di ![]() nella coppia
nella coppia
![]() è arbitraria. Questo si potrebbe mostrare ripetendo
il ragionamento con una scelta diversa delle formule di
Green nel piano
è arbitraria. Questo si potrebbe mostrare ripetendo
il ragionamento con una scelta diversa delle formule di
Green nel piano ![]() e/o nel piano
e/o nel piano ![]() , ma anche più
direttamente componendo una trasformazione definita da
, ma anche più
direttamente componendo una trasformazione definita da
![]() con una trasformazione che scambia la coordinata
con il momento, in uno dei due piani (o in entrambi).
con una trasformazione che scambia la coordinata
con il momento, in uno dei due piani (o in entrambi).
Naturalmente occorre aggiustare i segni: se si esegue
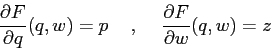
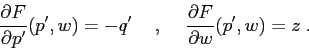
Se si esegue la trasformazione
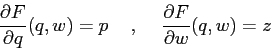
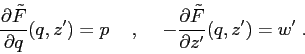
Finalmente, eseguendo due scambi coordinata/momento, uno
nel piano ![]() ed uno nel piano
ed uno nel piano ![]() , si ottiene una
quarta formula con funzione generatrice
, si ottiene una
quarta formula con funzione generatrice
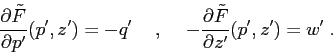
Esempio:
che definisce con le sue equazioni di Hamilton
l'oscillatore armonico:
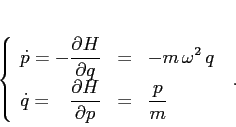
Applichiamo a questo sistema hamiltoniano la trasformazione
canonica
![]() definita dalla funzione generatrice:
definita dalla funzione generatrice:
ossia
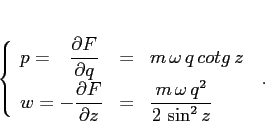
Per esplicitare la trasformazione inversa
![]() ricaviamo
ricaviamo ![]() dalla seconda equazione:
dalla seconda equazione:
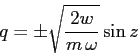
e quindi sostituiamo nella prima:
La costante ![]() nella definizione di
nella definizione di ![]() è stata
scelta per ottenere la semplificazione di
è stata
scelta per ottenere la semplificazione di ![]() che risulta sostituendo:
che risulta sostituendo:
e quindi nelle variabili ![]() il flusso integrale, in
funzione della condizione iniziale
il flusso integrale, in
funzione della condizione iniziale ![]() , è dato da
uno scorrimento:
, è dato da
uno scorrimento:
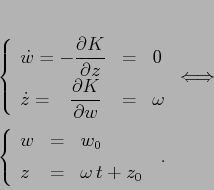
Sostituendo nella trasformazione inversa si ottiene
esplicitamente la soluzione anche nelle variabili ![]() :
:
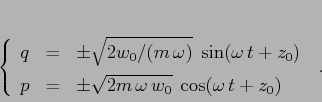
Resta il problema di decidere la scelta dei segni nella
soluzione; per confronto con la soluzione nota
dell'oscillatore lineare, che è una rotazione con velocità
angolare ![]() nel piano
nel piano ![]() (si noti lo scambio,
essenziale per avere rotazione antioraria per
(si noti lo scambio,
essenziale per avere rotazione antioraria per ![]() positivo) si può concludere che la scelta di due segni
positivo) si può concludere che la scelta di due segni ![]() oppure due segni
oppure due segni ![]() è giusta. Però a questa conclusione
non si può arrivare sulla base della funzione generatrice
scelta, che definisce una trasformazione definita solo per
è giusta. Però a questa conclusione
non si può arrivare sulla base della funzione generatrice
scelta, che definisce una trasformazione definita solo per
![]() . Questo è un esempio del fatto che le proprietà
globali delle trasformazioni canoniche vanno studiate caso per
caso, senza farsi trascinare dal formalismo puramente locale
delle funzioni generatrici.
. Questo è un esempio del fatto che le proprietà
globali delle trasformazioni canoniche vanno studiate caso per
caso, senza farsi trascinare dal formalismo puramente locale
delle funzioni generatrici.
Andrea Milani 2009-06-01