4.2 METODO DI EULERO

Sommario Il più semplice procedimento per approssimare un sistema dinamico continuo con uno discreto è quello di Eulero. Le soluzioni del sistema discreto così ottenuto approssimano le soluzioni del sistema continuo, in un senso che può essere reso rigoroso con la nozione di convergenza uniforme. La differenza tra le due, cioè l'errore di discretizzazione, è una funzione rapidamente crescente con il passare del tempo, per cui la potenza di calcolo richiesta per ottenere soluzioni accurate è notevole.

Metodo di Eulero nel caso lineare

Una definizione alternativa della funzione esponenziale di variabile reale è:

$$\lim_{m\to +\infty} \left(1+\frac{at}{m}\right)^m =e^{at}\ .$$

Vale l'analogo matriciale: se $A$ è una matrice quadrata $n\times n$:

$$\exp(A\,t)=\lim_{m\to +\infty} \left(I +\frac {A\,t}m\right)^m$$

per ogni $t$ in ${\bf R}$. Basta scrivere la differenza

$$\exp(A\,t) - \left(I +\frac {A\,t}m\right)^m = \sum_{k=0}^\... ...1{k!} - \left({m\atop k}\right)\frac 1{m^k}\right]\, A^k\, t^k$$

(i coefficienti binomiali sono nulli quando $k>m$); la serie a secondo membro ha coefficienti non negativi, e se si passa alle norme si trova la maggiorazione

$$\left \Vert \exp(A\,t) - \left (I +\frac {A\,t}m\right )^m\r... ...{a\,\vert t\vert} - \left(1+\frac{a\,\vert t\vert}{m}\right)^m$$

dove $a=\vert\vert A\vert\vert$ è la norma uniforme della matrice $A$. Nel caso scalare la successione converge uniformemente sull'intervallo $[-t,t]$, con $t$ arbitrario (ma fissato). Per il teorema della convergenza in norma, anche la definizione alternativa di esponenziale nel caso matriciale converge uniformemente su $[-t,t]$. Da questo segue (per una delle proprietà della norma uniforme) che

$$\exp(A\,t)\,X_0 = \lim_{m\to +\infty} \left(I +\frac {A\,t}m\right)^m\,X_0$$

uniformemente per $t$ in ogni intervallo limitato, e per ogni condizione iniziale $X_0$. L'aspetto interessante di questa formula è che al primo membro abbiamo il flusso integrale di un sistema dinamico continuo lineare; a secondo membro sotto segno di limite abbiamo l'analoga rappresentazione di tutte le soluzioni di un sistema dinamico discreto lineare, e precisamente

$$\frac{d{X}}{d{t}} = A\, X \hspace{5mm},\hspace{5mm}X_{k+1}=\left(I +\frac {A\,t}m\right)\,X_k\;.$$

La relazione tra il sistema dinamico continuo e quello discreto ottenuta qua sopra è un caso particolare (lineare) del metodo di Eulero. La motivazione geometrica dell'approssimazione di Eulero può essere apprezzata dalla Figura 4.3. Se si deve calcolare la soluzione con condizione iniziale $X(0)=X_0$ al tempo $t=\delta$, si suddivide l'intervallo $[0,\delta]$ in cui varia $t$ in $m$ sottointervalli, ciascuno di lunghezza pari al passo d'integrazione $h=\delta/m$, con $m$ abbastanza grande. Allora si approssima $X(\delta/m)$ con $X_1=X_0+hA\,X_0$, $X(2\delta/m)$ con $X_2=X_1+hA\,X_1$, eccetera, ad ogni passo rimpiazzando la vera soluzione con la sua approssimazione lineare (cioè con il suo differenziale).

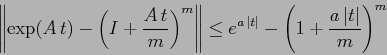
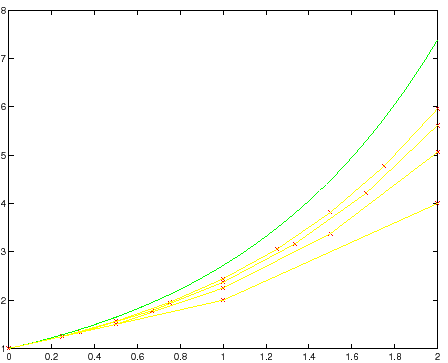
Benché nel sistema dinamico discreto appaiano solo i punti che approssimano la soluzione ai tempi $t=k\delta/m$ con $k$ intero, si può immaginare di descrivere un'approssimazione per tutti i tempi $t\in [0,\delta]$ usando l'interpolazione lineare (cioè ancora lo stesso differenziale) per i punti intermedi. Il poligono di Eulero ottenuto congiungendo i punti $(k\delta/m, X_k)$ è il grafico di una funzione di $t$ che è continua ma non differenziabile, e che approssima la soluzione nel senso che la successione di poligoni di Eulero ottenuti per $m$ crescente tende alla soluzione del sistema dinamico continuo, uniformemente su $[0,\delta]$.

Figura 4.3: Il poligono di Eulero: ad ogni passo temporale si approssima la soluzione del sistema dinamico continuo con il suo differenziale nel punto precedentemente calcolato; in questo esempio la soluzione dell'equazione y'=y è approssimata con il metodo di Eulero usando 2,4,6 ed 8 passi.

L'errore di troncamento locale commesso in un passo di lunghezza $h>0$ del metodo di Eulero al posto della soluzione esatta si può maggiorare usando il confronto in norma con l'esponenziale:

$$\vert\vert\exp(Ah)-(I+Ah)\vert\vert\leq e^{a\,h}-(1+ah)= \fr... ...2\,h^2}2\, e^{a\,\theta\,h}\leq \frac{a^2\,h^2}2\, e^{a\,h}\;,$$

dove $a=\vert\vert A\vert\vert$ e $0<\theta<1$; il penultimo passaggio è il resto di Lagrange della formula di Taylor per la funzione esponenziale di variabile reale.

Esempio:

Il sistema dinamico lineare che si vuole approssimare sia un oscillatore armonico:

$$\left\{\begin{array}{lcl} {\displaystyle \dot x} & {\disp... ...}\right]\;\left[\begin{array}{c}{x}\\ {y}\end{array}\right]$$



Il metodo di Eulero dà il sistema dinamico discreto:


$$\left[\begin{array}{c}{x_{k+1}}\\ {y_{k+1}}\end{array}\ri... ...ght)\;\left[\begin{array}{c}{x_k}\\ {y_k}\end{array}\right]$$



La soluzione del sistema discreto contiene le potenze della matrice $(I-\omega\,h\,J)$, e quindi si scrive più facilmente interpretando questa matrice come numero complesso, e poi usando la rappresentazione mediante modulo e argomento:

$$\begin{eqnarray*} \vert I-\omega\,h\,J\vert&=&\left(1+\omega^2\,h^2\right)^{1/2... ...\omega^2\,h^2\right)^{k/2}\,(\cos k\theta -J\,\sin k\theta)\;, \end{eqnarray*}$$





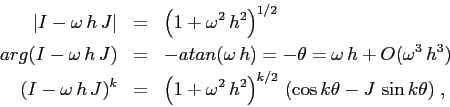
In conclusione la matrice che esprime la soluzione al passo $k$ in funzione delle condizioni iniziali è una dilatazione di un fattore


$$\left(1+\omega^2\,h^2\right)^{k/2}=1+ k\,\frac{\omega^2\,h^2}2 + O(\omega^4\,h^4)$$


che è vicino a uno per $\omega\,h$ piccolo, seguita da una rotazione di un angolo

$$-\theta=-\omega\, h+ O(\omega^3\,h^3)$$


che differisce di poco dalla rotazione di $-\omega\,h$ della soluzione del sistema continuo, sempre per $\omega\,h$ piccolo.

Esercizio Discretizzare, con il metodo di Eulero, il sistema dinamico

$$\dot x = \omega\,y \hspace{5mm},\hspace{5mm}\dot y = \omega \,x$$

e discutere l'andamento delle soluzioni per il tempo discreto che tende a $\pm\infty$. (Soluzione)

Convergenza del metodo di Eulero

Supponiamo di dover approssimare la soluzione di un sistema dinamico nonlineare $\dot X = F(X)$ con condizione iniziale $X(0)=X_0$. Il metodo di Eulero consiste nell'approssimare la soluzione al tempo $h$ con l'approssimazione lineare:

$$X(h)\simeq X_1 = X_0 + h\,F(X_0)$$

La soluzione a tempi successivi può essere approssimata ripetendo il procedimento, cioè con la successione definita per ricorrenza:

$$\left\{\begin{array}{lcl} {\displaystyle X_0} & {\displays... ...ystyle=} &{\displaystyle X_k + h\, F(X_k)} \end{array}\right.$$

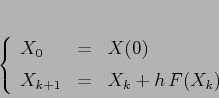
Se si desidera avere delle informazioni sui valori assunti da $X(t)$ per valori di $t$ intermedi tra $kh$ e $(k+1)h$ si può ricorrere ad un'interpolazione, per esempio lineare ottenendo ancora il poligono di Eulero. L'errore di troncamento locale è sempre infinitesimo del secondo ordine rispetto ad $h$:

$$X(t+h)= X(t) + h\,\dot X(t) + O(h^2) \ .$$

L'errore di troncamento accumulato è la differenza tra la successione definita per ricorrenza dal metodo di Eulero e la soluzione del sistema dinamico con le stesse condizioni iniziali:

$$\Delta^{(k)}=X(k\,h)-X_k \ .$$

Se il campo vettoriale $F(X)$ è lipschitziano di costante $L$ e limitato in modulo dalla costante $M$, cioè se

$$\vert F(X)-F(Y)\vert\leq L\,\vert X-Y\vert \hspace{5mm},\hspace{5mm}\vert F(X)\vert \leq M$$

per ogni $X,Y$ in ${\bf R}^n$, allora l'errore accumulato $\Delta^{(k)}$ dopo il tempo $t=k\,h$ soddisfa alla diseguaglianza

$$\vert\Delta^{(k)}\vert=\delta_k\leq M\,h\,\left [e^{\sqrt{n}\, L\, t}-1 \right]\;.$$

Dimostrazione:

Lo stato sia $X=(x_j)$ ed il campo vettoriale $F(X)= f_j(X)$, con $j=1, n$; la soluzione al passo $k+1$ si può calcolare con la formula di Lagrange:

$$x_j(k\,h +h)=x_j(k\,h)+h\,f_j\left(X(k\,h+\theta_j\,h)\right)$$


dove per ogni $j$ va scelto un $\theta_j$ con $0<\theta_j<1$. Si noti che ciascuno dei punti $X(k\,h+\theta_j\,h)$ non può distare da $X(k\,h)$ più di $h\,M$, sempre per la formula di Lagrange. Nal passare da $X_k$ a $X_{k+1}=X_k+h\,F(X_k)$ l'errore di troncamento accumulato si accresce secondo la formula:

$$\Delta^{(k+1)}_j=\Delta^{(k)}_j + h\,f_j\left(X(k\,h+\theta_j\,h)\right)-h\,f_j(X_k)\;.$$


Si passa ai valori assoluti, si usa la diseguaglianza triangolare; la differenza, nella formula precedente, tra i valori di $F$ calcolati in due punti diversi si può maggiorare con $L$ volte la norma della differenza degli argomenti, si ottiene

$$\vert\Delta^{(k+1)}_j\vert\leq \vert\Delta^{(k)}_j\vert + h\, L \left[h\,M+ \delta_k\right]$$




$$\delta_{k+1}\leq \delta_k +\sqrt{n}\,h\,L\,[h\,M +\delta_k]$$


Definiamo un'altra successione $\epsilon_k$ che sia soluzione della stessa equazione ma con il segno di uguaglianza, e con $\epsilon_0=\delta_0=0$:

$$\epsilon_{k+1}= \epsilon_k +\sqrt{n}\,h\,L\,[h\,M +\epsilon_k]\;.$$


Allora $\delta_k\leq \epsilon_k$, ma la successione $\epsilon_k$ è soluzione di un'equazione alle differenze finite lineare non omogenea, e si può calcolare esplicitamente

$$\epsilon_k=\alpha [1+\sqrt{n}\, h\, L]^k +\beta\ .$$


La costante $\beta$ è una soluzione dell'equazione non omogenea e si ricava per sostituzione:

$$\beta = \beta +\sqrt{n}\,h\,L\,[h\,M +\beta] \Longrightarrow \beta= -h\,M$$


e imponendo la condizione iniziale $\epsilon_0=0$ si trova $\alpha= -\beta=h\,M.$ In conclusione

$$\delta_k\leq \epsilon_k = h\, M \left[ (1+h\,\sqrt{n}\, L)^k -1 \right]\;.$$


Per ottenere la tesi basta sostituire $t=k\,h$ ed usare la diseguaglianza

$$(1+h\,\sqrt{n}\, L)^k=\left(1 + {\sqrt{n}\, L\,t}/k\right)^k \leq e^{ \sqrt{n}\, L\,t}\;.$$



Il fattore $\sqrt{n}$ appare perché si sono usate nella dimostrazione due norme, quella euclidea per la lunghezza degli spostamenti, e quella di matrice che è contenuta nella relazione tra matrice jacobiana e costante di Lipschitz.

 C.D.D.

La maggiorazione per l'errore di troncamento accumulato che si ricava in generale, cioè per ogni possibile sistema dinamico, si rivela pessimistica in casi specifici. Che l'accumulazione dell'errore possa essere esponenziale è inevitabile, ma in molti casi l'esponente sarà più piccolo della costante di Lipschitz, e sarà piuttosto legato al massimo esponente di Lyapounov della soluzione che si cerca di approssimare.