4.1 DIFFERENZE FINITE LINEARI

Sommario Un sistema alle differenze finite lineari si risolve calcolando le potenze di una matrice; questo calcolo diventa molto più semplice se la matrice è ridotta alla forma canonica di Jordan. Modelli alle differenze finite lineari sono impiegati in molti campi; qui diamo degli esempi tratti dalla modellizzazione di fenomeni economici.

Equazioni lineari alle differenze prime

Un sistema dinamico discreto lineare in ${\bf R}^n$ è della forma:

$$X_{k+1}=A\, X_k$$

dove $A$ è una matrice $n\times n$ invertibile ed $\{X_k\}, k\in {\bf Z}$ è l'orbita. L'orbita può essere descritta mediante le potenze di $A$:

$$X_k=A^k\,X_0\hspace{5mm},\hspace{5mm}k\in {\bf Z}$$

però il calcolo esplicito di una potenza elevata di una matrice richiede un gran numero di operazioni aritmetiche (per di più, questo numero cresce con il cubo della dimensione $n$).

Si può allora cercare di semplificare questo calcolo mediante un cambiamento di coordinate lineare: se $Y_k=B\,X_k$ è la stessa orbita vista in un nuovo sistema di coordinate, associate alla base $\{V_1,\ldots, V_n\}$ mediante la matrice $V$ con colonne $V_j$ (si ricorda che in tal caso $B$ è invertibile, e $B^{-1}=V$), allora

$$Y_k=B\,X_k=B\,A^k\,X_0= B\,A^k\,B^{-1}\,Y_0= \left(B\,A\,B^{-1}\right)^k\,Y_0$$

Quindi nel nuovo sistema di coordinate $Y=B\,X$ il sistema dinamico discreto ha per matrice $D=B\,A\,B^{-1}$ e per soluzione $Y_k=D^k\,Y_0$; se la nuova base è scelta in modo che il calcolo delle potenze di $D$ sia più semplice, allora converrà esprimere la soluzione passando attraverso $Y_k$, cioè:

$$X_k=B^{-1}\,Y_k=B^{-1}\,D^k\,B\,X_0$$

Per esempio, se la matrice $A$ è diagonalizzabile, allora possiamo scegliere la nuova base in modo che $D=diag[\lambda_j]$, dove $\lambda_j,\; j=1,\ldots,n$ sono gli autovalori di $A$ (che sono tutti reali). Allora la soluzione nello spazio delle coordinate $Y$ sarà semplicemente

$$Y_k=D^k\,Y_0= diag[\lambda_j]^k\,Y_0= diag[\lambda_j^k]\,Y_0\;,$$

e, tornando alle coordinate $X$,

$$X_k=B^{-1}\,diag[\lambda_j^k]\,B\,X_0\;;$$

ogni coordinata di $X_k$ è una combinazione lineare, a coefficienti dipendenti dalla condizione iniziale, dei monomi $\lambda_j^k$ formati con gli autovalori di $A$.

L'analogia con il caso continuo è così stretta che non vale la pena di ripetere la discussione dei vari casi di autovalori coniugati, di una matrice semisemplice e con parte nilpotente; si può passare direttamente al risultato generale, utilizzando la forma canonica di Jordan.

Uso della forma canonica di Jordan

Per il teorema della decomposizione S + N la matrice $A$ può comunque essere descritta come somma di una matrice semisemplice $S$ ed una matrice nilpotente $N$, che commutano tra loro: $SN=NS$. Allora vale la formula del binomio di Newton:

$$A^k=\sum_{i=0}^k \left({k \atop i}\right) S^{k-i}\,N^i\;.$$

In questo modo il calcolo delle potenze è semplificato, e può essere descritto in ogni caso in termini di polinomi.

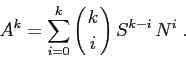
Per ogni matrice $A$ di tipo $n\times n$, le soluzioni di $X_{k+1}=A\,X_k$ hanno componenti che si possono esprimere come combinazioni lineari delle seguenti successioni:

• $\lambda_i^k$, dove $\lambda_i$ è un autovalore reale di $A$.

• $\lambda_i^k \, P_i(k)$, dove $P_i(k)$ è un polinomio di grado $< r_i$ nella variabile $k$, e $\lambda_i$ è un autovalore reale di $A$ di molteplicità $r_i$.

• $Re(z_i^k), Im(z_i^k)$, dove $z_i, \overline z_i$ sono autovalori complessi coniugati di $A$.

• $Re(z_i^k)\,P_i(k),\; Im(z_i^k)\, P_i(k)$, dove $P_i(k)$ è un polinomio di grado $< r_i$ nella variabile $k$, e $z_i, \overline z_i$ sono autovalori complessi coniugati di $A$ di molteplicità $r_i$.

  Si noti che i coefficienti del polinomio $P_i$ dipendono da $\lambda_i$. Se si vuole esprimere la dipendenza da $\lambda_i$, e non da $k$, si può usare l'espressione $Q_i(\lambda_i)$ dove $Q_i$ è un polinomio di grado $k$ che contiene monomi di grado $\geq k-r_i$.

Dimostrazione:

Supponiamo che la nuova base $\{V_j\}$ sia stata scelta in modo che $D=V\,A\,V^{-1}$ sia in forma canonica di Jordan reale: allora $D=S+N$ con $S$ una matrice che ha sulla diagonale gli autovalori reali, e per ogni coppia di autovalori complessi coniugati $(z,\overline z)$ la matrice $2\times 2$ che rappresenta $z$; la matrice nilpotente $N$ è in questo caso diagonale a blocchi con blocchi in forma canonica del nilpotente. Allora esaminiamo l'espressione della soluzione:

$$X_k=B^{-1}\,Y_k=B^{-1}\,D^k\,B\,X_0= B^{-1}\,\sum_{i=0}^k \left({k \atop i}\right) S^{k-i}\,N^i\;B \, X_0$$


prendendo in considerazione i blocchi di Jordan che si riferiscono a ciascuno dei quattro casi (radici reali e complesse, semplici e multiple). Nel caso di radici semplici appare solo la potenza $k$-esima dell'autovalore (inteso come matrice $2\times 2$ nel caso complesso). Nel caso di radici multiple, la conclusione segue dall'osservazione che

$$\left({k \atop i}\right)= \frac{k\,(k-1)\, (k-2)\,\ldots\,(k-i+1)} {i\, (i-1)\, (i-2)\,\ldots\, 1}$$


è un polinomio di grado $i$ nella variabile $k$.

 C.D.D.

Stabilità

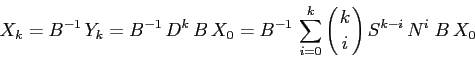
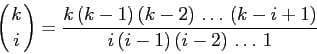
Definizione:

Si dice che l'applicazione $F\colon{\bf R}^n\to{\bf R}^n$ è una mappa stabile nel punto $X_0$ se per ogni $\epsilon>0$ esiste un $\delta >0$ tale che:

$$\vert X-X_0\vert<\delta\Rightarrow \vert F^k(X)-F^k(X_0)\vert<\epsilon\ {\rm per\ ogni\ } k\in {\bf N}\ .$$


$F$ è una mappa instabile in $X_0$ se e solo se non è stabile.

Si dice che $F\colon{\bf R}^n\to{\bf R}^n$ è una mappa asintoticamente stabile nel punto $X_0$ se è stabile, ed inoltre esiste un intorno $U$ di $X_0$ tale che


$$X\in U \Rightarrow \lim\limits_{k\to\infty}\vert F^k(X)-F^k(X_0)\vert=0\;.$$

Supponiamo che $F\colon{\bf R}^n\to{\bf R}^n$ sia un'applicazione lineare, cioè $F(X)=A\,X$ con $A$ una matrice $n\times n$. Poiché le successioni $A^k\, X$ contengono le potenze $k$-esime degli autovalori, la stabilità della soluzione nulla $X_0=\underline 0$ è controllata dai moltiplicatori di Lyapounov, che sono i moduli degli autovalori: l'applicazione lineare è asintoticamente stabile nel punto $X_0=\underline 0$ se e solo se tutti i moltiplicatori di Lyapounov sono minori di $1$.

Avere tutti i moltiplicatori di Lyapounov $\leq 1$ è necessario, ma non sufficiente per la stabilità della soluzione nulla; infatti in presenza di autovalori multipli di modulo $1$ possono essere presenti termini a crescenza polinomiale nell'indice $k$.

L'analogia con il teorema del pozzo lineare può essere resa esplicita definendo, in questo caso, gli esponenti di Lyapounov come i logaritmi naturali dei moltiplicatori di Lyapounov, cioè come i numeri reali $\log \vert\mu\vert$ per ogni autovalore $\mu$ della matrice $A$ del sistema dinamico discreto lineare.

Questa seconda definizione di esponenti di Lyapounov è coerente con la precedente, nel senso che segue. Se $\dot X =AX$ è un sistema dinamico continuo lineare, ed i suoi esponenti di Lyapounov sono $Re(\lambda)$, con $det[A-\lambda\,I]=0$, consideriamo il sistema dinamico discreto lineare ottenuto per discretizzazione con passo $h$:

$$X_{k+1}=B\, X_k \hspace{5mm},\hspace{5mm}B=\exp(Ah)\;.$$

Allora $B$ ha per autovalori $\exp(\lambda\,h)$ e per moltiplicatori di Lyapounov i moduli

$$\mu=\vert\exp(\lambda\,h)\vert=\exp\left[Re(\lambda)\,h\right]\; ,$$

e i suoi esponenti di Lyapounov sono $\log \mu=Re(\lambda)\,h$.

Vale anche il risultato analogo dei teoremi del pozzo nonlineare e della sorgente nonlineare:

Sia $X_{k+1}=f(X_k)$ un sistema dinamico discreto, $X_0$ un punto fisso, tale che $f(X_0)=X_0$, e $A$ la matrice jacobiana di $f$ in $X_0$. Se tutti i moltiplicatori di Lyapounov di $A$ sono minori di 1, allora $f$ è asintoticamente stabile in $X_0$; se tutti i moltiplicatori di Lyapounov sono maggiori di 1, $f^{-1}$ è asintoticamente stabile in $X_0$.
Dimostrazione omessa.

Equazioni alle differenze finite

In generale, una successione può essere definita per ricorrenza da una funzione di un certo numero di valori precedenti; per esempio si parla di equazione alle differenze finite di ordine 2 quando

$$X_{k+2}=F(X_{k+1},X_k)$$

cioè ogni nuovo termine è definito dai due precedenti. È sempre possibile ricondurre un'equazione alle differenze finite ad un sistema dinamico. Per esempio nel caso di ordine 2 si considera un vettore di stato consistente di due termini successivi:

$$V_k=\left[\begin{array}{c}{X_{k+1}}\\ {X_k}\end{array}\right]$$

e si definisce un sistema dinamico discreto in questo modo:

$$\left[\begin{array}{c}{X_{k+2}}\\ {X_{k+1}}\end{array}\rig... ...{array}{c}{F(X_{k+1},X_k)}\\ {X_{k+1}}\end{array}\right] \ .$$

Esempio:

L'equazione alle differenze finite lineare del secondo ordine

$$a\,x_{k+2}+b\, x_{k+1} +c\, x_k=0$$


(con $a\neq 0$) si trasforma nel sistema dinamico discreto lineare

$$\left[\begin{array}{c}{x_{k+2}}\\ {x_{k+1}}\end{array}\rig... ...,\left[\begin{array}{c}{x_{k+1}}\\ {x_{k}}\end{array}\right]$$


con per matrice la matrice compagna $A$ che ha equazione caratteristica

$$\frac 1a \left[ a\,\lambda^2 + b\, \lambda +c\right]=0$$


e quindi la soluzione in funzione della condizione iniziale $(x_0,x_1)$

$$\left[\begin{array}{c}{x_{k+1}}\\ {x_k}\end{array}\right]=A^k\, \left[\begin{array}{c}{x_1}\\ {x_0}\end{array}\right]$$


avrà per moltiplicatori di Lyapounov i moduli delle radici dell'equazione polinomiale con gli stessi coefficienti dell'equazione alle differenze finite.

Esercizio Studiare i seguenti problemi alle differenze finite lineari del secondo ordine:

1. Numeri di Fibonacci:
   
   $$\left\{\begin{array}{l} {\displaystyle x_{k+2}=x_{k+1}+x_k}\\ [2mm] {\displaystyle x_0=1\;,\;x_1=1} \end{array}\right.\;;$$
   
   

2. Per $k\to\infty$, è limitata la soluzione di
   
   $$\left\{\begin{array}{l} {\displaystyle x_{k+2}=2x_{k+1}-4x_k}\\ [2mm] {\displaystyle x_0=0\;,\;x_1=1} \end{array}\right.\;?$$
   
   

3. Discutere nel piano $\{x_0,x_1\}$ il comportamento delle soluzioni di $x_{k+2}=2x_{k+1}-x_k$.

(Soluzione)

Esempi di modelli economici alle differenze finite

Diamo di seguito alcuni esempi di modelli di fenomeni economici mediante equazioni alle differenze finite lineari. Gli esempi citati sono microeconomici, cioè descrivono la legge della domanda e dell'offerta per un singolo bene su di un dato mercato; esistono però anche modelli alle differenze finite di fenomeni macroeconomici, cioè dell'andamento di un intera economia.

Esempio:

Il modello della ragnatela dell'equilibrio di un mercato è un sistema dinamico discreto lineare in ${\bf R}^3$, con tre variabili $(p,s,d)$ la cui interpretazione è la seguente:

$p$
è il prezzo (si intende di un certo bene).
$s$
è l'offerta.
$d$
è la domanda.

Il tempo è discreto, $t\in {\bf Z}$ (come è logico perché i fenomeni economici non possono essere istantanei).

Le equazioni del modello sono le seguenti:

(1)

equazione della domanda:

$$d_t=a-b\,p_t\;,$$

dove $a,b>0$ sono costanti assegnate. $a$ è il consumo a prezzo zero, cioè il massimo consumo utile al consumatore, $b$ è l'elasticità della domanda; $a/b$ rappresenta il prezzo massimo (oltre il quale il consumo è nullo).

(2)

equazione della produzione:

$$s_t=c+f\,p_{t-1} \;,$$

dove $c\leq 0$ (se il prezzo è zero, nessuno produce), ed $f>0$ misura la risposta del produttore all'aumento di prezzo.

(3)

equazione di equilibrio di mercato: nel modello della ragnatela questa è la più semplice possibile, cioè:

$$s_t=d_t$$

per cui domanda ed offerta sono sempre in equilibrio, senza ritardi. Ne segue che il modello può essere considerato come sistema dinamico in ${\bf R}^2$.

Figura 4.1: Modello della ragnatela: nel caso stabile, la soluzione converge all'equilibrio. Per ogni passo temporale abbiamo disegnato prima il cambiamento di prezzo e poi quello dell'offerta che ne consegue.

Si può comprendere dall'equazione (2) che l'unità di tempo corrisponde al tempo necessario per la produzione; per esempio può essere un anno per i prodotti agricoli che possono essere seminati e raccolti solo una volta all'anno.

Allora si può ricavare una singola equazione alle differenze finite per la variabile $p$ che rappresenta il prezzo:

$$p_t= -\frac fb \, p_{t-1} +\frac {a-c}b \;,$$

e la seconda variabile ($d=s$) si può dedurre da (1) (o da (2)), in funzione di $p_t$. L'equazione alle differenze finite per la variabile prezzo è non omogenea, cioè ha un secondo membro indipendente dalle variabili dinamiche, funzione solo di $k$. In questo caso però il secondo membro è costante; perciò l'equazione ha una soluzione costante, $p_t=k$ con

$$k= -\frac fb \,k +\frac {a-c}b\hspace{5mm},\hspace{5mm}k=\frac{a-c}{b+f}$$

a cui bisogna aggiungere la soluzione generale dell'equazione omogenea:

$$p_t= -\frac fb \, p_{t-1}\longrightarrow p_t=\left(-\frac fb\right)^t \, \alpha$$

dove la costante $\alpha$ è arbitraria; si può quindi scegliere $\alpha$ in modo da soddisfare alla condizione iniziale $p_0$:

$$p_t=k + \left(-\frac fb\right)^t\,(p_0-k)\; .$$

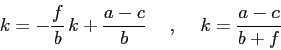
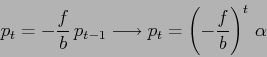
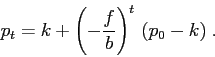
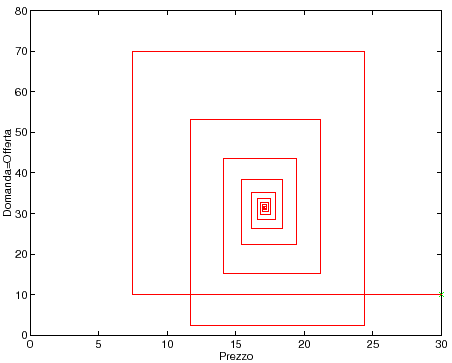
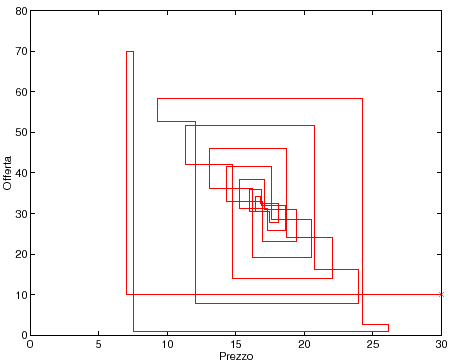
Qualitativamente la soluzione è un'oscillazione ($-f/b<0$) che è smorzata se $f/b<1$, amplificata se $f/b>1$; nel primo caso la soluzione tende a $p=k, s=d=c+f\,k$ per $t\to +\infty$, seguendo un percorso che ha l'aspetto di una ragnatela (se si congiunge ogni punto dell'orbita con il successivo mediante due segmenti paralleli agli assi, vedi Figura 4.1).

Esempio:

Il modello delle scorte si ottiene modificando, nel modello della ragnatela, l'equazione di equilibrio di mercato, assumendo che domanda ed offerta possano non essere in equilibrio e generare delle scorte $u_t$; allora l'equazione (3) è rimpiazzata da:

(4)
equazione delle scorte:


$$u_t-u_{t-1}=s_t-d_t\;,$$




che descrive l'accrescimento delle scorte con l'invenduto.

(5)
equazione del prezzo:


$$p_{t+1}-p_t=-g[u_t-u_{t-1}]\;,$$




dove la costante $g>0$ descrive come l'invenduto fa calare il prezzo.

Figura 4.2: Modello delle scorte: con gli stessi valori dei parametri a,b,c,f della figura precedente, la soluzione converge all'equilibrio. Poiché però il prodotto $f\,g$ è appena minore di uno, prezzi e offerta tendono all'equilibrio in modo più laborioso.

Possiamo sintetizzare le equazioni (1), (2), (4) e (5) in un'unica equazione alle differenze finite di ordine 2 per la variabile prezzo:

$$p_{t+1}-(1-bg)\,p_t+fg\,p_{t-1}=(a-c)g$$

che ha la soluzione particolare costante $p_t=k$ data dall'equazione:

$$k-(1-bg)\,k+fg\,k=(a-c)g\Longrightarrow k=\frac{a-c}{b+f}$$

ossia il prezzo di equilibrio è lo stesso del modello della ragnatela. L'equazione omogenea:

$$p_{t+1}-(1-bg)\,p_t+fg\,p_{t-1}=0$$

è equivalente al sistema dinamico discreto:

$$\left[\begin{array}{c}{p_{t+1}}\\ {p_t}\end{array}\right]=... ...\; \left[\begin{array}{c}{p_t}\\ {p_{t-1}}\end{array}\right]$$

e quindi ha soluzioni che dipendono dalle radici dell'equazione caratteristica:

$$\lambda^2 -(1-bg)\,\lambda+fg=0$$

che possono essere reali o complesse, a seconda del segno del discriminante. La stabilità asintotica del prezzo, cioè la convergenza per $t\to +\infty$ al prezzo di equilibrio, è assicurata soltanto se i moduli di entrambe le radici (cioè i moltiplicatori di Lyapounov) sono $<1$. In ogni caso il prodotto delle radici è il numero reale $fg>0$, e se $fg>1$ nella soluzione di equilibrio è certamente una mappa instabile (troppa avidità e troppa paura!).