6.4 REGIONI ORDINATE

Sommario In ogni intorno di un punto fisso ellittico di un sistema conservativo esistono, sotto ipotesi che si verificano nella maggior parte dei casi, delle curve invarianti chiuse. Queste curve invarianti formano una regione ordinata in cui sono anche presenti moti caotici, che però sono intrappolati in anelli delimitati da curve invarianti e perciò non possono dare luogo ad instabilità su larga scala. In questa Sezione vengono presentati risultati non facili, senza dimostrazioni (che si potrebbero trovare in [Siegel-Moser 71]).

Forma normale dei punti fissi ellittici

Si consideri un punto fisso ellittico $X^*$ di un sistema dinamico discreto $S$ su ${\bf R}^2$ (oppure ${\bf T}^2$), differenziabile (supponiamo, per semplicità, di classe $C^\infty$) e conservativo. Il linearizzato di $S$ in $X^*$ ha (per definizione di punto fisso ellittico) autovalori $\exp(\pm i \beta)$, complessi coniugati di modulo 1 ( $\beta\neq j\pi, j\in {\bf Z}$). Vogliamo porre la mappa $S$ in una forma normale che la approssimi, in un intorno di $X^*$, in un modo semplice e geometricamente espressivo.

Possiamo supporre, a meno di traslazioni, che $X^*=(0,0)$, e a meno di cambiamenti di coordinate lineari che il linearizzato in $(0,0)$ sia proprio

$$D S(0,0)=\exp(J\beta)=\left[\begin{array}{cc}{\cos\beta}&{-\sin\beta}\\ {\sin\beta}&{\cos\beta}\end{array}\right]\ .$$

Per semplificare la descrizione di mappe vicine a delle rotazioni usiamo delle coordinate polari canoniche, che preservano il carattere conservativo del sistema dinamico discreto.

$$\left\{\begin{array}{lcl} {\displaystyle x} & {\displaysty... ...isplaystyle \sqrt{2\,R'}\;\sin\theta'} \end{array}\right. \ .$$

In coordinate cartesiane $S(x,y)=(x',y')$, ma in coordinate polari

$$\left\{\begin{array}{lcl} {\displaystyle R'} & {\displayst... ...isplaystyle=} &{\displaystyle g(R,\theta)} \end{array}\right.$$

con $f\,g$ funzioni differenziabili (almeno per $R>0$).

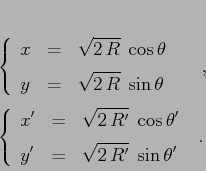
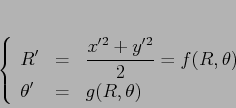
Per ogni punto fisso ellittico di un sistema dinamico discreto conservativo esiste un cambiamento di coordinate differenziabile che porta la mappa nella forma canonica:

$$\left\{\begin{array}{lcl} {\displaystyle R'} & {\displayst... ... \theta+\beta +\alpha R +{\cal O}(R^2)} \end{array}\right.\ .$$

Il coefficiente costante $\alpha$ si chiama la torsione del punto fisso ellittico.

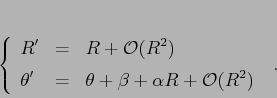
In questo modo la mappa viene ad essere approssimata, a meno di termini di ordine 2 in $R$ (quindi infinitesimi del quarto ordine rispetto ad $x,y$ per $(x,y)\to (0,0)$), da una mappa che ha come curve invarianti le circonferenze $R=cost$. In questa approssimazione la mappa ruota ogni circonferenza di un angolo funzione del raggio. Il numero di giri di cui ogni circonferenza viene ruotata, cioè $(\beta+\alpha R+ \ldots)/2\pi$, si chiama numero di rotazione.

Esempio:

Nella mappa standard del pendolo il punto $X_1=(0,0)$ ha linearizzato

$$A= \left[\begin{array}{cc}{1-h^2}&{1}\\ {-h^2}&{1}\end{array}\right]$$



ed autovalori

$$\lambda^2 -(2-h^2)\lambda +1 =0 \Longrightarrow \lambda= 1-\frac{h^2}2 \pm ih\sqrt{1-h^2/4}$$


complessi di modulo 1 (per $\vert h\vert<2$). Per il valore di $h$ usato nelle figure delle Sezioni precedenti, $h=1$, gli autovalori sono $\exp(\pm i\,2\pi/6)$, cioè gli autovalori sono radici dell'unità di ordine 6 e la matrice $A$ è ottenuta per coniugio da una rotazione di un sesto di giro. Perciò la forma normale di Birkhoff è

$$\left\{\begin{array}{lcl} {\displaystyle R'} & {\displayst... ...\frac{2\pi}6 +\alpha R +{\cal O}(R^2)} \end{array}\right. \ ;$$


il calcolo della torsione $\alpha$ non è immediato, ma $\alpha<0$.

Curve invarianti

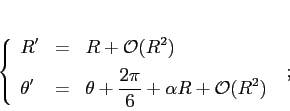
Le circonferenze che vengono mandate in se stesse dall'approssimazione della forma normale di Birkhoff sono esempi di curve invarianti di rotazione, la cui definizione generale è come segue.

Definizione:

Una curva invariante di Moser è una curva chiusa, cioè una parametrizzazione differenziabile $\gamma: S^1 \to {\bf R}^2$ (oppure ${\bf T}^2$), iniettiva e tale che per ogni valore della variabile angolo $\phi$


$$S(\gamma(\phi))=\gamma(\phi+\mu)\ .$$


La curva chiusa non è soltanto invariante, ma la restrizione della mappa $S$ ai punti nell'immagine della curva è coniugata (mediante la parametrizzazione) ad una rotazione; $\mu/2\pi$ è il numero di rotazione.

Il teorema della forma normale di Birkhoff non assicura l'esistenza di curve invarianti di Moser, ma soltanto che la mappa è vicina, a meno di infinitesimi di ordine superiore, ad un'altra mappa geometricamente più semplice per cui ogni circonferenza è una curva invariante. L'esistenza di curve invarianti di rotazione ``esatte'' per la mappa conservativa data è conseguenza di un teorema più difficile, di cui diamo l'enunciato di seguito.

Sia $X^*$ un punto fisso ellittico di un sistema dinamico discreto conservativo. Se gli autovalori del linearizzato $\lambda, \overline\lambda$ sono tali che $\lambda^k\neq 1$ per $k=3,4$, e la forma normale di Birkhoff ha torsione non nulla, allora in ogni intorno di $X^*$ si trova una curva invariante di Moser.

$\lambda^k\neq 1$ per $k=1,2$ fa parte della definizione di punto fisso ellittico. Quindi l'ipotesi del teorema implica che gli autovalori del linearizzato non sono radici dell'unità di ordine minore di 5.

Le curve invarianti del teorema di Moser ``girano attorno'' al punto fisso ellittico, cioè ognuna di esse è il bordo di un intorno di $X^*$.

Esempio:

Il punto fisso ellittico $X_2=(0,0)$ della mappa standard del pendolo per $h=1$ è circondato da curve invarianti di Moser, e la mappa è stabile (Figura 6.13).

Figura 6.13: Curve invarianti nell'intorno del punto fisso ellittico, per $h=1$. Si noti che l'angolo di rotazione è molto vicino a $2\pi /6$ per le curve vicine al punto fisso.

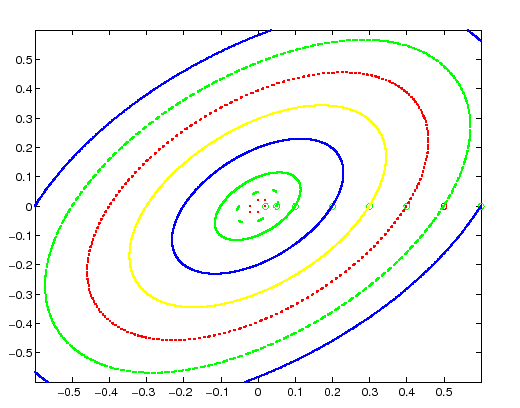Esempio:

Condideriamo nella mappa standard del pendolo $S$ con $h=1$ il punto di periodo 2 ellittico $X_3=(0,\pi)$. Esso è un punto fisso ellittico per la mappa $S^2$, con linearizzato ed autovalori



$$A^{(2)}=\left[\begin{array}{cc}{-1}&{3}\\ {-1}&{2}\end{arr... ...1=0 \Longrightarrow \lambda= \frac 12 \pm i\,\frac{\sqrt{3}}2$$


che non sono radici dell'unità di ordine minore di 6. Andrebbe verificato che la torsione è $\neq 0$, comunque la Figura 6.1 sembra indicare la presenza di curve invarianti di Moser in un intorno non tanto piccolo dei punti $X_3$ e $X_4=S(X_3)$.

Regioni ordinate

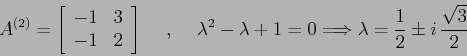
L'insieme delle immagini delle curve invarianti di Moser forma una regione ordinata.

Figura 6.14: Anche per $h=0.5$ le curve invarianti, benché sembrino occupare una buona parte del toro, non riempiono alcun aperto. Tra le due curve invarianti del tipo circolazione ci sono delle isole che circondano delle orbite di periodo tre.

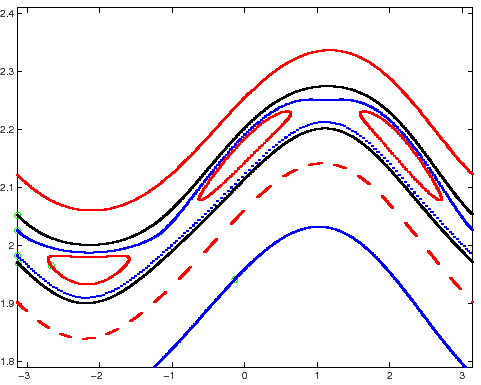Il senso di questa definizione è chiaro nel caso del flusso integrale per un certo tempo $h>0$ di un sistema dinamico continuo di tipo hamiltoniano, perchè il sistema è integrabile. Le regioni formate da orbite periodiche, descritte da variabili azione-angolo, sono regioni ordinate, sia nel caso delle librazioni che delle circolazioni.

Purtroppo questa definizione non è molto utile nei casi non integrabili perchè l'unione delle curve invarianti di Moser è molto difficile da descrivere; per di più si tratta di un insieme senza parte interna, quindi impiegare la parola ``regione'' confonde le idee. La Figura 6.14 illustra il meccanismo che spezza la continuità dell'insieme delle curve invarianti di Moser: tra due di tali curve vi è una regione invariante, a forma di corona circolare, che a sua volta conterrà orbite periodiche, con punti periodici ellittici (nel cui intorno ci saranno curve invarianti, ma che ``girano attorno'' al punto periodico) ed iperbolici, con le loro separatrici, i loro punti omoclinici ed eteroclinici, in conclusione con la loro regione caotica.

Se invece si vuole usare una definizione meno forte di regione ordinata, ammettendo che essa possa contenere anche del caos, purchè ``la maggior parte'' delle orbite stia su curve invarianti di Moser, si incontrano gravi difficoltà a dare una definizione che sia rigorosa.