Next: 5. SISTEMI CONSERVATIVI Up: 4. DISCRETIZZAZIONE Previous: 4.3 DISCRETIZZAZIONE CONSERVATIVA Indice Indice analitico
Sommario Quando un sistema dinamico non è integrabile mediante
un'espressione analitica esplicita, il che si verifica nella
stragrande maggioranza dei casi, può essere necessario usare un
procedimento che fornisca un'approssimazione della soluzione. Un
metodo di integrazione numerica è quindi un algoritmo che definisce
un sistema dinamico discreto le cui soluzioni ![]() approssimano la
soluzione del sistema dinamico continuo su una successione di
tempi, per esempio
approssimano la
soluzione del sistema dinamico continuo su una successione di
tempi, per esempio
![]() . Esistono moltissimi metodi di
integrazione numerica, e qui presentiamo soltanto i più semplici,
commentando i rispettivi vantaggi e svantaggi.
. Esistono moltissimi metodi di
integrazione numerica, e qui presentiamo soltanto i più semplici,
commentando i rispettivi vantaggi e svantaggi.
Come si è visto nella dimostrazione del teorema della mappa standard, gli scorrimenti sono mappe conservative del piano in se stesso. Perciò, se si vuole in qualche modo approssimare un sistema continuo conservativo con un sistema discreto pure conservativo, si possono cercare dei metodi di approssimazione che consistano in una sequenza di scorrimenti. Questi metodi vanno sotto il nome di metodi simplettici a scorrimento. Per esempio la mappa standard è un metodo simplettico a due scorrimenti.
Per integrare il sistema dinamico derivato da un sistema newtoniano di
dimensione 1
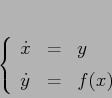
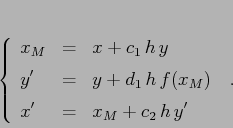
Cerchiamo quindi di determinare i tre coefficienti ![]() in modo
che il metodo abbia ordine di troncamento 2, cioè con
errore di troncamento locale
in modo
che il metodo abbia ordine di troncamento 2, cioè con
errore di troncamento locale ![]() . Per ottenere questo, basta
imporre che risolva esattamente il caso
. Per ottenere questo, basta
imporre che risolva esattamente il caso ![]() , con soluzione per
esempio
, con soluzione per
esempio ![]() :
:
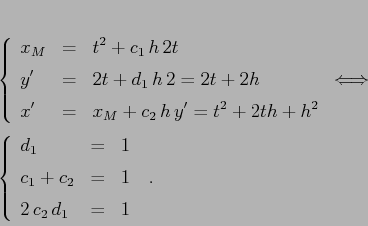
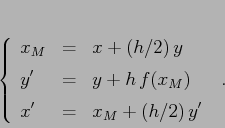
Esempio:
 |
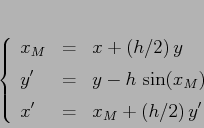
Esercizio
Nell'esempio precedente, mostrare che i punti fissi sono ancora
![]() e
e ![]() . (Soluzione)
. (Soluzione)
Una classe importante di metodi di integrazione numerica va sotto il
nome di Runge e Kutta. Dato il sistema dinamico
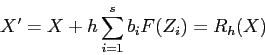
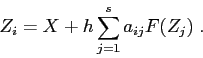
Se la matrice ![]() è tale che
è tale che ![]() per
per ![]() , il
metodo è esplicito ed i valori
intermedi
, il
metodo è esplicito ed i valori
intermedi ![]() si possono calcolare in sequenza, altrimenti il metodo
è implicito e le equazioni per gli
si possono calcolare in sequenza, altrimenti il metodo
è implicito e le equazioni per gli
![]() vanno risolte ad ogni passo. La soluzione di questo sistema di
equazioni esiste ed è unica per
vanno risolte ad ogni passo. La soluzione di questo sistema di
equazioni esiste ed è unica per ![]() abbastanza piccolo; infatti si
tratta di un'equazione del tipo del punto unito, e per
abbastanza piccolo; infatti si
tratta di un'equazione del tipo del punto unito, e per ![]() piccolo il secondo membro è una contrazione (in un intorno di
piccolo il secondo membro è una contrazione (in un intorno di ![]() ).
).
Lo stesso metodo si potrebbe applicare anche ad un sistema di
equazioni differenziali non autonomo
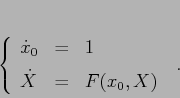
Questo significa usare la formula modificata per il calcolo dei
valori intermedi
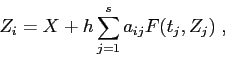
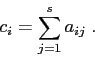
Per imporre che il metodo sia di ordine ![]() si può richiedere che
risolva esattamente le equazioni differenziali che hanno come
soluzioni dei polinomi di grado fino a
si può richiedere che
risolva esattamente le equazioni differenziali che hanno come
soluzioni dei polinomi di grado fino a ![]() : in altri termini le equazioni
: in altri termini le equazioni
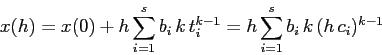
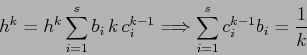
Si noti che se i ![]() sono già stati scelti, questo è un sistema
lineare con incognite
sono già stati scelti, questo è un sistema
lineare con incognite ![]() e come matrice dei
coefficienti la matrice di Vandermonde
e come matrice dei
coefficienti la matrice di Vandermonde
![]() ;
il sistema è quadrato se si richiede che l'ordine sia
;
il sistema è quadrato se si richiede che l'ordine sia ![]() , e in tal
caso ha soluzione unica se i
, e in tal
caso ha soluzione unica se i ![]() sono diversi tra loro (perché il
determinante della matrice di Vandermonde
sono diversi tra loro (perché il
determinante della matrice di Vandermonde ![]() è diverso da zero).
è diverso da zero).
Vediamo allora alcune soluzioni di queste equazioni: per esempio, se
cerchiamo un metodo di ordine 2 a 2 passi intermedi, abbiamo un sistema
di due equazioni in quattro incognite
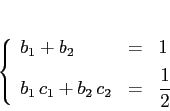
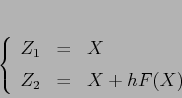
Se invece cerchiamo un metodo ad un solo passo intermedio e di ordine
2, è chiaro che non potrà essere esplicito (avendo una matrice ![]() di tipo
di tipo ![]() , questa non può essere nulla sulla diagonale,
altrimenti è nulla e si ottiene un metodo di ordine 1). Abbiamo
allora due equazioni, nelle due sole incognite
, questa non può essere nulla sulla diagonale,
altrimenti è nulla e si ottiene un metodo di ordine 1). Abbiamo
allora due equazioni, nelle due sole incognite ![]() :
:
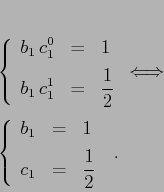
La soluzione in questo caso è unica, con ![]() ; il metodo è
implicito, nel senso che il valore intermedio appare nell'equazione
del punto unito:
; il metodo è
implicito, nel senso che il valore intermedio appare nell'equazione
del punto unito:
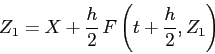
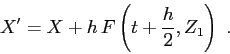
Il metodo di Runge-Kutta implicito ad un passo intermedio ha notevoli proprietà qualitative, delle quali la più importante è quella del teorema seguente.
Il metodo di Runge-Kutta implicito ad 1 passo intermedio e di ordine 2 è conservativo, nel senso che se applicato ad un sistema newtoniano ad un grado di libertà fornisce un sistema dinamico discreto conservativo.
Dimostrazione omessa.
 |
Esempio:
Applichiamo il metodo di Runge-Kutta implicito di ordine 2 e ad un
solo passo intermedio al pendolo nonlineare conservativo
![]() . Ponendo come al solito
. Ponendo come al solito ![]() , l'equazione del
punto unito per il valore intermedio
, l'equazione del
punto unito per il valore intermedio ![]() è
è
![\begin{displaymath}
\left[\begin{array}{c}{x_M}\\
{y_M}\end{array}\right]= \le...
...ft[\begin{array}{c}{y_M}\\
{-\sin(x_M)}\end{array}\right]\;;
\end{displaymath}](img1495.png)
![\begin{displaymath}
\left[\begin{array}{c}{x'}\\
{y'}\end{array}\right]=\left[...
...ft[\begin{array}{c}{y_M}\\
{-\sin(x_M)}\end{array}\right]\;.
\end{displaymath}](img1496.png)
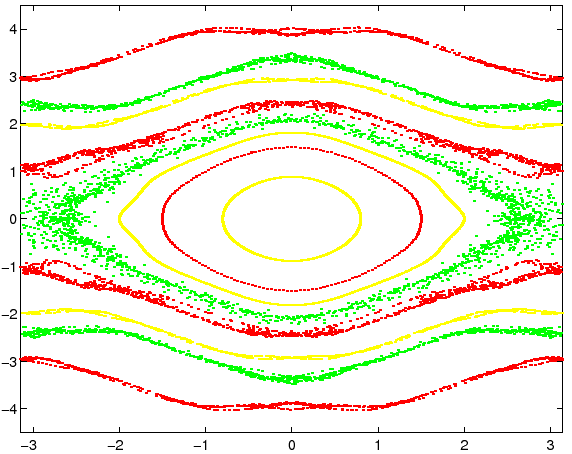
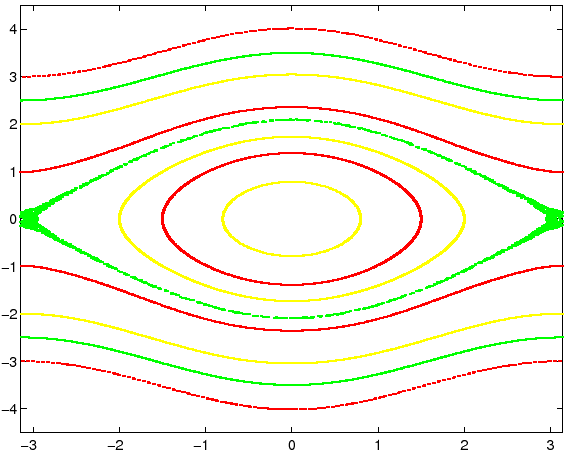
Poiché il sistema dinamico così ottenuto è conservativo,
le proprietà di stabilità delle approssimazioni lineari sono
conservate; anche alcune proprietà qualitative, come la presenza di
curve invarianti, sono conservate, e la regione caotica che circonda
la separatrice è di area molto ridotta, persino per valori di ![]() che con altri metodi di discretizzazione danno una larga regione
caotica, per esempio
che con altri metodi di discretizzazione danno una larga regione
caotica, per esempio ![]() (Figura 4.8).
(Figura 4.8).
La ragione per cui questo metodo è particolarmente efficace
nel generare una piccola regione caotica attorno alla separatrice ha a
che fare con un'altra proprietà aggiuntiva rispetto a quella di
essere conservativo: i metodi di questa classe (di ordine ![]() ad
ad ![]() passi intermedi, come il metodo di Runge-Kutta-Gauss) hanno
la proprietà di preservare esattamente le forme quadratiche che
siano integrali primi. Quindi nell'intorno del punto di sella
nonlineare il comportamento delle soluzioni è descritto in modo
molto accurato, perché nell'equazione linearizzata ci sarebbe un
integrale primo quadratico.
passi intermedi, come il metodo di Runge-Kutta-Gauss) hanno
la proprietà di preservare esattamente le forme quadratiche che
siano integrali primi. Quindi nell'intorno del punto di sella
nonlineare il comportamento delle soluzioni è descritto in modo
molto accurato, perché nell'equazione linearizzata ci sarebbe un
integrale primo quadratico.
Costruire metodi con ordine di troncamento superiore al
secondo non è tanto facile, ma si conoscono molte
soluzioni. Prendiamo per esempio l'ordine 4: il
metodo di Runge-Kutta classico
(il primo ad essere stato scoperto, ed ancora
largamente in uso) è di ordine 4 con 4 passi intermedi, e con la
seguente scelta dei tempi intermedi:
![]() .
.
 |
Da qui il sistema di 4 equazioni lineari nelle 4 incognite ![]()
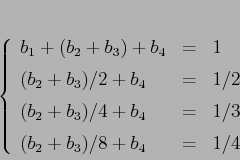
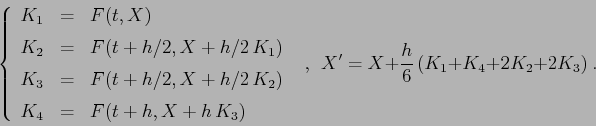
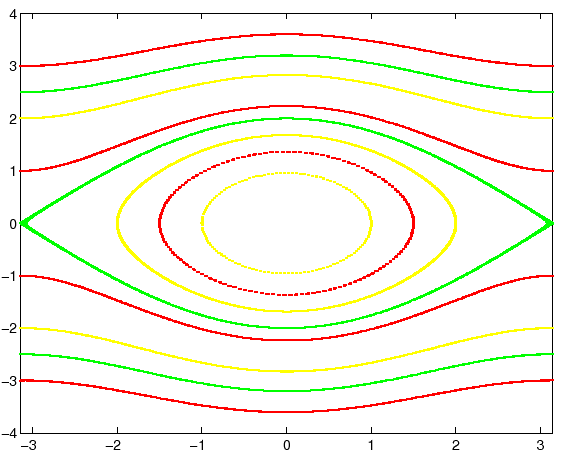
Un metodo del quarto ordine, anche se non è conservativo, può essere usato con un passo abbastanza piccolo per ottenere soluzioni che siano quantitativamente molto simili a quelle esatte (Figura 4.9). Bisogna però fare attenzione a non usare il risultato dell'integrazione numerica per dedurne delle proprietà qualitative; per esempio, in un sistema newtoniano si introduce una ``dissipazione numerica''.
A titolo di esempio di un metodo ancora più accurato, che però richiede
un numero maggiore di valutazioni del secondo membro per ogni passo,
diamo i coefficienti dell'unico metodo implicito di ordine 4 a due
passi intermedi, detto metodo di Runge-Kutta-Gauss:
![\begin{displaymath}\left\{\begin{array}{lcl}
{\displaystyle c_1} & {\displays...
...sqrt{3})/12}\\
{(3+2\sqrt{3})/12}&{1/4}\end{array}\right]\;.
\end{displaymath}](img1503.png)
Anche il metodo di Gauss è una discretizzazione conservativa, ed ha proprietà di stabilità molto forti: per esempio, fornisce una mappa stabile se usato per un sistema lineare stabile. Per una trattazione completa delle proprietà note dei metodi di integrazione numerica di Runge-Kutta si veda [Butcher 87].
Esercizio
Per esercitarsi sui metodi di integrazione numerica occorre usare un
calcolatore. Dato un sistema newtoniano ![]() , e scelto un
linguaggio di programmazione con capacità grafiche, si scrivano e si
collaudino (osservando le orbite rappresentate graficamente) programmi
che eseguano le seguenti discretizzazioni:
, e scelto un
linguaggio di programmazione con capacità grafiche, si scrivano e si
collaudino (osservando le orbite rappresentate graficamente) programmi
che eseguano le seguenti discretizzazioni:
Andrea Milani 2009-06-01