Next: 3.6 SELLE Up: 3. TEORIA QUALITATIVA Previous: 3.4 SISTEMI NEWTONIANI Indice Indice analitico
Sommario Se un campo vettoriale ![]() è il gradiente di una funzione
è il gradiente di una funzione
![]() , il sistema dinamico definito da
, il sistema dinamico definito da ![]() ammette
ammette ![]() come funzione
di Lyapounov globale, e si possono calcolare esplicitamente tutti i
bacini di attrazione. Quindi per i sistemi dinamici gradiente è
particolarmente semplice, nella maggior parte dei casi, discutere
l'esistenza delle soluzioni per ogni
come funzione
di Lyapounov globale, e si possono calcolare esplicitamente tutti i
bacini di attrazione. Quindi per i sistemi dinamici gradiente è
particolarmente semplice, nella maggior parte dei casi, discutere
l'esistenza delle soluzioni per ogni ![]() , i punti limite e la
stabilità degli equilibri.
, i punti limite e la
stabilità degli equilibri.
Definizione:
![\begin{displaymath}
\dot X =F(X)=-grad^T\, U(X)=-\left[\frac{\partial {U}}{\par...
... {x_2}},\ldots,
\frac{\partial {U}}{\partial {x_n}}\right]^T
\end{displaymath}](img937.png)
Il simbolo di trasposto è necessario perché il
gradiente è un vettore riga, mentre ![]() è un
vettore colonna. Per semplificare la
notazione si usa il simbolo
è un
vettore colonna. Per semplificare la
notazione si usa il simbolo
![]() che indica
il gradiente come vettore colonna, cioè
il vettore colonna con le derivate parziali come componenti.
che indica
il gradiente come vettore colonna, cioè
il vettore colonna con le derivate parziali come componenti.
 |
La funzione ![]() si indica anche con il nome di
potenziale del campo vettoriale conservativo
si indica anche con il nome di
potenziale del campo vettoriale conservativo
![]() ; si faccia però attenzione a non confondere il potenziale
dei sistemi gradienti, che è il potenziale di un campo
vettoriale opposto alle velocità, con l'opposto dell'energia
potenziale (per unità di massa) nei sistemi newtoniani, che è
il potenziale del campo vettoriale che esprime l'accelerazione.
; si faccia però attenzione a non confondere il potenziale
dei sistemi gradienti, che è il potenziale di un campo
vettoriale opposto alle velocità, con l'opposto dell'energia
potenziale (per unità di massa) nei sistemi newtoniani, che è
il potenziale del campo vettoriale che esprime l'accelerazione.
Il campo vettoriale
![]() è perpendicolare in ogni
punto alle superfici di livello
è perpendicolare in ogni
punto alle superfici di livello ![]() (per il teorema della
funzione implicita; si veda la Figura 3.6), e
si annulla solo nei punti stazionari della funzione
(per il teorema della
funzione implicita; si veda la Figura 3.6), e
si annulla solo nei punti stazionari della funzione ![]() , che sono
anche punti di equilibrio per il sistema dinamico gradiente. La
stabilità di questi punti di equilibrio può essere studiata
utilizzando sia il metodo della funzione di Lyapounov che quello della
linearizzazione nei punti di equilibrio.
, che sono
anche punti di equilibrio per il sistema dinamico gradiente. La
stabilità di questi punti di equilibrio può essere studiata
utilizzando sia il metodo della funzione di Lyapounov che quello della
linearizzazione nei punti di equilibrio.
Un sistema dinamico gradiente è dotato in modo naturale di funzioni
di Lyapounov, che sono semplicemente
![]() . Infatti la
derivata totale
. Infatti la
derivata totale
e si annulla solo nei punti di equilibrio. Perciò ogni punto ![]() di
minimo locale non degenere per
di
minimo locale non degenere per ![]() è un punto di equilibrio
asintoticamente stabile per il sistema dinamico gradiente, con
funzione di Lyapounov stretta
è un punto di equilibrio
asintoticamente stabile per il sistema dinamico gradiente, con
funzione di Lyapounov stretta ![]() . La
disponibilità di una funzione di Lyapounov ``globale'' consente di
ottenere conclusioni molto precise anche sui limiti e sui bacini di
attrazione.
. La
disponibilità di una funzione di Lyapounov ``globale'' consente di
ottenere conclusioni molto precise anche sui limiti e sui bacini di
attrazione.
Sia ![]() una soluzione del sistema gradiente
una soluzione del sistema gradiente
![]() definito sull'aperto
definito sull'aperto ![]() , tale da mantenersi per
ogni
, tale da mantenersi per
ogni ![]() dentro un compatto
dentro un compatto ![]() contenuto in
contenuto in
![]() . Supponiamo inoltre che i punti di equilibrio del sistema
dinamico (cioè i punti stazionari di
. Supponiamo inoltre che i punti di equilibrio del sistema
dinamico (cioè i punti stazionari di ![]() ) siano isolati. Allora
il limite per
) siano isolati. Allora
il limite per ![]() della soluzione
della soluzione ![]() esiste, ed è
un punto stazionario di
esiste, ed è
un punto stazionario di ![]() .
.
Dimostrazione:
Resta da provare che il valore limite è un solo punto di equilibrio. Poiché i punti di equilibrio sono isolati, l'insieme dei valori limite non può contenerne più di uno per non essere sconnesso, il che contraddirebbe il teorema di invarianza degli insiemi limite.
Poiché la funzione di Lyapounov ![]() è globale, cioè vale
su tutto l'insieme
è globale, cioè vale
su tutto l'insieme ![]() su cui è definito il sistema dinamico, è
possibile dare delle descrizioni globali dei bacini di attrazione in
termini dei valori di
su cui è definito il sistema dinamico, è
possibile dare delle descrizioni globali dei bacini di attrazione in
termini dei valori di ![]() . Supponiamo per esempio che
. Supponiamo per esempio che ![]() sia un punto
di minimo locale non degenere (quindi isolato) per
sia un punto
di minimo locale non degenere (quindi isolato) per ![]() , e che
, e che
![]() sia il valore di questo minimo: allora per ogni
sia il valore di questo minimo: allora per ogni
![]() l'insieme
l'insieme
Esempio:
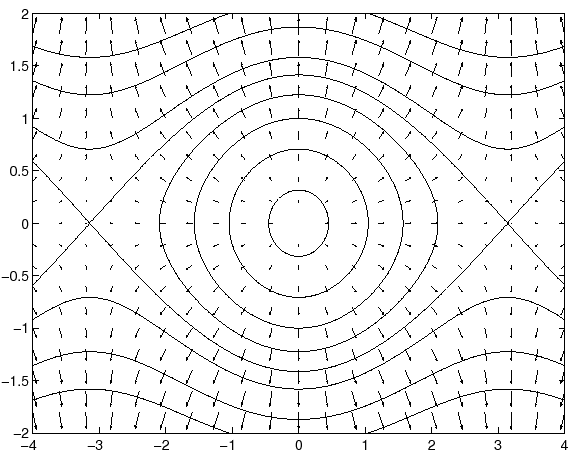
Il sistema dinamico gradiente che ha ![]() come potenziale
come potenziale
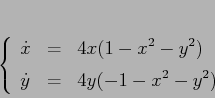
 |
Un'altra proprietà caratteristica dei sistemi dinamici gradienti è
che i sistemi linearizzati nei punti di equilibrio sono descritti da
matrici simmetriche. Se
![]() , ed
, ed
![]() :
:
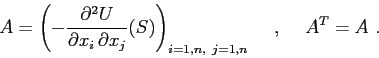
Per il teorema di diagonalizzazione delle forme quadratiche
gli autovalori di una matrice simmetrica sono tutti
reali, quindi coincidono con gli esponenti di Lyapounov del
sistema linearizzato nel punto stazionario. Perciò si ha un
pozzo dove la matrice hessiana è definita positiva (cioè
quando ![]() ha un minimo non degenere), ed una sorgente dove
ha un minimo non degenere), ed una sorgente dove ![]() ha un
massimo non degenere. In tutti i casi in cui esistono autovalori con segni
discordi si ha una situazione come quella della sella, cioè
un punto stazionario per
ha un
massimo non degenere. In tutti i casi in cui esistono autovalori con segni
discordi si ha una situazione come quella della sella, cioè
un punto stazionario per ![]() che non è un estremo ha un bacino,
ma non sta nella parte interna del suo bacino.
che non è un estremo ha un bacino,
ma non sta nella parte interna del suo bacino.
Esercizio
Consideriamo i sistemi dinamici gradiente in ![]() :
:
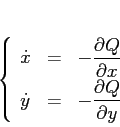
dove ![]() è una forma quadratica omogenea non
degenere. Dimostrare che possono avere un solo punto di equilibrio,
e che questo può essere soltanto del tipo nodo o sella, ma né
centro, né fuoco, né nodo improprio.
(Soluzione)
è una forma quadratica omogenea non
degenere. Dimostrare che possono avere un solo punto di equilibrio,
e che questo può essere soltanto del tipo nodo o sella, ma né
centro, né fuoco, né nodo improprio.
(Soluzione)
Esercizio
Studiare il sistema
![\begin{displaymath}
\frac{d{}}{d{t}} \left[\begin{array}{c}{x}\\
{y}\end{array...
...array}{c}{-2xy+y^2+y}\\
{-x^2+x+2xy-2y}\end{array}\right]\;.
\end{displaymath}](img974.png)
Andrea Milani 2009-06-01