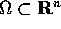 un aperto,
un aperto, 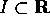 un intervallo,
un intervallo,
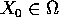 e
e
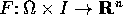 un
campo vettoriale uniformemente lipschitziano nella prima
variabile. Allora se due soluzioni continue
un
campo vettoriale uniformemente lipschitziano nella prima
variabile. Allora se due soluzioni continue 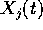 (j=1,2) del
problema
(j=1,2) del
problema
Sommario Il teorema di esistenza assicura la soluzione di un problema con condizione iniziale data solo per un piccolo intervallo sull'asse dei tempi. La soluzione può essere prolungata rispetto al tempo fino ad un intervallo massimale; se questo ha un estremo finito, allora la soluzione esce da ogni compatto contenuto nell'insieme di definizione.
Teorema di continuazione delle soluzioni :
Siano 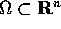 un aperto,
un aperto, 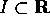 un intervallo,
un intervallo,
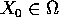 e
e
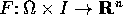 un
campo vettoriale uniformemente lipschitziano nella prima
variabile. Allora se due soluzioni continue
un
campo vettoriale uniformemente lipschitziano nella prima
variabile. Allora se due soluzioni continue 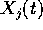 (j=1,2) del
problema
(j=1,2) del
problema
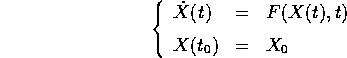
sono definite sullo stesso intervallo 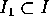 contenente
contenente 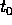 ,
esse coincidono su
,
esse coincidono su 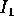 . Perciò
. Perciò
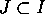 contenente
contenente
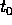 , sul quale è definita la soluzione X(t) del problema (nel
senso che gli intervalli nei quali sono definite le soluzioni locali
del problema sono contenuti in J);
, sul quale è definita la soluzione X(t) del problema (nel
senso che gli intervalli nei quali sono definite le soluzioni locali
del problema sono contenuti in J);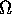 (se la
soluzione è limitata allora tende alla frontiera di
(se la
soluzione è limitata allora tende alla frontiera di 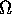 ).
).
Dimostrazione:
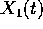 e
e 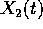 risolvono il problema per
risolvono il problema per 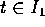 ,
l'unicità locale garantisce che esse coincidono almeno in
un intorno
,
l'unicità locale garantisce che esse coincidono almeno in
un intorno 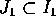 di
di 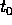 , anzi esiste l'intervallo
, anzi esiste l'intervallo 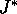 più
grande sul quale
più
grande sul quale 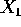 e
e 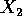 coincidono:
coincidono: 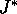 è l'unione di tutti
i
è l'unione di tutti
i 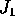 , ovvero
, ovvero
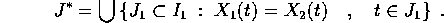
Inoltre 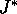 deve coincidere con
deve coincidere con 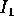 : altrimenti esisterebbe un
estremo
: altrimenti esisterebbe un
estremo 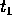 di
di 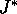 , appartenente a
, appartenente a 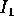 ,
tale che
,
tale che 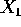 e
e 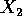 potrebbero essere prolungate dapprima fino a
potrebbero essere prolungate dapprima fino a 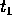 (per continuità
(per continuità 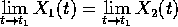 ), poi oltre
), poi oltre 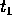 (applicando il teorema di esistenza ed
unicità locale al problema con punto iniziale
(applicando il teorema di esistenza ed
unicità locale al problema con punto iniziale 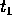 ); sarebbe così\
definito un intervallo più grande di
); sarebbe così\
definito un intervallo più grande di 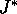 sul quale
sul quale 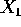 e
e 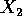 coincidono, contraddicendo la definizione di
coincidono, contraddicendo la definizione di 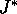 .
.
Una soluzione locale X(t) passante per 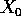 al tempo
al tempo 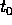 può
dunque essere prolungata in un intervallo
massimale
può
dunque essere prolungata in un intervallo
massimale 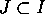 , ottenuto dall'unione tutti gli intervalli
contenenti
, ottenuto dall'unione tutti gli intervalli
contenenti 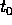 nei quali esistono soluzioni locali del
problema.
nei quali esistono soluzioni locali del
problema.
Per studiare il caso in cui J ha un estremo finito, supponiamo
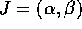 , con
, con 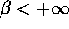 . Se la soluzione continua X(t) del
problema fosse limitata e non tendesse alla frontiera di
. Se la soluzione continua X(t) del
problema fosse limitata e non tendesse alla frontiera di 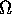 per
per
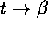 , esisterebbe un compatto
, esisterebbe un compatto 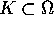 tale che
tale che
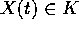 per ogni
per ogni 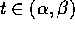 , ma allora si potrebbero
prolungare X(t) e la sua derivata oltre
, ma allora si potrebbero
prolungare X(t) e la sua derivata oltre 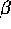 , contraddicendo la
massimalità di
J. Infatti
, contraddicendo la
massimalità di
J. Infatti
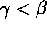 , X(t) e la sua derivata, definite su
, X(t) e la sua derivata, definite su
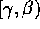 , potrebbero essere prolungate fino a
, potrebbero essere prolungate fino a 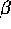 per
continuità: F è continua, perciò ha massimo M sul compatto
per
continuità: F è continua, perciò ha massimo M sul compatto
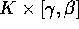 ; per
; per 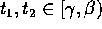 si ha
si ha
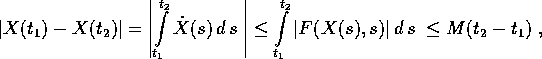
perciò X(t), uniformemente continua su 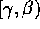 , potrebbe
essere prolungata fino a
, potrebbe
essere prolungata fino a 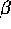 ; allora si potrebbe passare al limite
per
; allora si potrebbe passare al limite
per 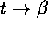 nell'uguaglianza
nell'uguaglianza
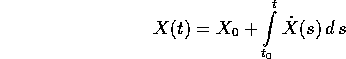
che varrebbe, per la continuità dell'integrale, anche per 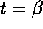 .
.
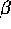 , sarebbero definite
anche fino a
, sarebbero definite
anche fino a 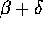 per un opportuno
per un opportuno 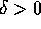 , in
contraddizione con la massimalità dell'intervallo
, in
contraddizione con la massimalità dell'intervallo 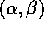 ,
,
Se il sistema dinamico è autonomo, cioè 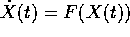 ,
per ogni condizione iniziale
,
per ogni condizione iniziale 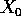 l'ampiezza dell'intervallo
massimale
l'ampiezza dell'intervallo
massimale 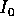 della soluzione
della soluzione 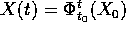 non dipende
dall'istante iniziale. Il flusso è infatti un
gruppo continuo locale ad un parametro di operatori su
non dipende
dall'istante iniziale. Il flusso è infatti un
gruppo continuo locale ad un parametro di operatori su
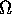 . Precisamente, traslando
. Precisamente, traslando 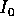 in
in 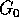 per condurre
per condurre 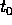 nell'origine dei tempi, la famiglia ad un indice di operatori
nell'origine dei tempi, la famiglia ad un indice di operatori

gode, per 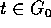 , delle proprietà di gruppo rispetto alla
composizione: per
, delle proprietà di gruppo rispetto alla
composizione: per 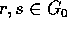 si ha
si ha 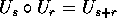 (se
Y(s)=X(r+s), per l'indipendenza di F da t risulta
(se
Y(s)=X(r+s), per l'indipendenza di F da t risulta
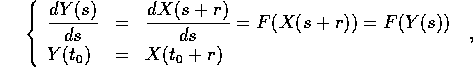
e per il teorema di
continuazione delle soluzioni Y(s)=X(r+s)); inoltre 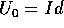 e se
e se
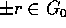 , allora
, allora 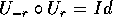 . In particolare,
. In particolare,
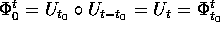 .
.