


Next: About this document
Up: SISTEMI DINAMICI
Previous: References
- ampiezze complesse
- Oscillatori lineari, Quasipolinomi, Ampiezze complesse
- angoli di Eulero
- Elementi orbitali, Integrabilità, Parametrizzare una rotazione
- anomalia eccentrica
- Orbite interplanetarie
- anomalia media
- Variabili di Delaunay, Orbite interplanetarie
- anomalia vera
- Elementi orbitali, Variabili di Delaunay, Orbite interplanetarie, Orbite interplanetarie
- apocentro
- Gli integrali classici, Problema dei due corpi
- apogeo
- Satelliti artificiali
- applicazione asintoticamente stabile
- Uso della forma canonica , Sistemi periodici
- applicazione stabile
- Uso della forma canonica , Sistemi periodici
- approssimazioni successive
- Dimensione 1, Metodi di Runge-Kutta, Metodi di Runge-Kutta, A.1 ESISTENZA E UNICITÀ
- argomento del pericentro
- Gli integrali classici, Problema dei due corpi , Elementi orbitali
- asintoticamente stabile
- Stabilità, Caso lineare, Caso nonlineare, Il metodo della funzione , Sistemi conservativi ad un , Sistemi con dissipazione, Wronskiano
- asse
- Isometrie
- assi d'inerzia
- Energia cinetica e momento , Equazioni di Eulero, Parametrizzare una rotazione
- assistenza gravitazionale
- Orbite interplanetarie, Costanti ed unità di
- attrattivo
- Stabilità
- autovalori
- Diagonalizzazione, Diagonalizzazione, Energia cinetica e momento , Polinomio caratteristico
- autovalori coniugati
- Centri e fuochi, Sistema semisemplice, Oscillatori lineari, Equazioni lineari alle differenze
- autovettori
- Diagonalizzazione, Polinomio caratteristico
- bacino
- Stabilità, Instabilità, Sistemi con dissipazione, Sistemi con dissipazione, Il potenziale come funzione , Punti stazionari ed hessiani
- bacino di attrazione
- Stabilità, Separatrici, Separatrici
- bacino di repulsione
- Separatrici
- battimento
- Ampiezze complesse
- Bertrand
- Problema dei due corpi
- binomio di Newton
- Serie prodotto, Uso della forma canonica , Discretizzazione di ordine superiore
- blocco di Jordan
- Un solo autovalore reale
- blocco di Jordan
- Un solo autovalore reale, Soluzione di un sistema , Ordine n, Caso lineare, Uso della forma canonica , Trasformazioni canoniche, Quasipolinomi, Forme canoniche
- blocco di Jordan reale
- Soluzione di un sistema , Forme canoniche
- bordo
- Funzioni generatrici, Integrali di lineaforme
- cambiamento di coordinate lineare
- Cambiamenti di coordinate, Un solo autovalore reale, Nodi impropri, Soluzione di un sistema , Oscillatori lineari, Equazioni lineari alle differenze
- cambiamento di scala
- Funzioni generatrici, Costanti ed unità di
- cambiamento di variabile negli integrali multipli
- Trasformazioni canoniche, Calcolo integrale in più
- campo vettoriale conservativo
- Equazioni di Newton, Integrali di lineaforme
- caos
- Mappa standard, Definizioni di caos
- capacità
- Circuiti elettrici lineari
- caratteristica di Eulero-Poincaré
- Due gradi di libertà, Varietà differenziabili
- carta coordinata
- Pendoli, Varietà differenziabili
- centro
- Centri e fuochi, Stabilità, Sistemi conservativi ad un
- centro di massa
- Integrali primi del problema , Riduzione alla forza centrale, Energia cinetica e momento , Caso continuo, Caso continuo
- chiuso
- Sistemi con dissipazione, Separatrici, 3.7 INSIEMI LIMITE, 3.7 INSIEMI LIMITE, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Variabili di Delaunay, Definizioni di caos, A.1 ESISTENZA E UNICITÀ, Topologia in
- ciclo limite
- Orbite periodiche
- cicloide
- Pendoli
- cilindro
- Parametrizzazione delle orbite periodiche, Superfici di rivoluzione
- circolazioni
- Parametrizzazione delle orbite periodiche
- coefficienti costanti
- 2.6 EQUAZIONI DI ORDINE , Oscillatori lineari, Ordine n, 8.2 EQUAZIONI LINEARI NON , Equazioni differenziali di ordine
- coefficienti quasi costanti
- Equazioni lineari a coefficienti
- commutano
- Serie prodotto
- commutazione
- Discretizzazione di ordine superiore
- compatto
- Norme di matrici, Convergenza dell'esponenziale, Il metodo della funzione , Il metodo della funzione , Sistemi con dissipazione, Il potenziale come funzione , Il potenziale come funzione , 3.7 INSIEMI LIMITE, 3.8 TEOREMA DI POINCARÉ-BENDIXON, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Variabili di Delaunay, Caso integrabile, A.1 ESISTENZA E UNICITÀ, Topologia in , Varietà differenziabili, B.4 SERIE DI FUNZIONI
- componenti connesse
- Sistemi con dissipazione, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Due gradi di libertà, Topologia in
- condizione iniziale
- 1.1 SISTEMI CONTINUI E , Dimensione 1, Dimensione 1, Sistemi lineari, Sistemi lineari, Sistemi lineari, Caso continuo, Cambiamenti di coordinate, 2.6 EQUAZIONI DI ORDINE , 3.1 STABILITÀ, Metodo di Eulero nel , Riduzione alla forza centrale, 8.1 OMOGENEIZZAZIONE
- condizioni ai limiti
- Oscillatori lineari
- condizioni iniziali
- 2.6 EQUAZIONI DI ORDINE , Oscillatori lineari, Ordine n, Ordine n, Equazioni differenziali di ordine
- coniugio
- Cambiamenti di coordinate, Nodi impropri
- connesso
- Sistemi con dissipazione, 3.7 INSIEMI LIMITE, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Topologia in
- cono di precessione
- Equazioni di Eulero
- conserva l'area
- Caso continuo, Caso discreto, Mappa standard, Le mappe che conservano , Equazioni lineari a coefficienti , Mappa di Poincaré, Calcolo integrale in più
- conserva l'orientazione
- Funzioni generatrici, Calcolo integrale in più
- conservativo
- Caso continuo, Differenze centrali, I sistemi hamiltoniani sono , Equazioni di Newton, Flussi canonici, Flussi canonici, Soluzioni del capitolo 3
- contrazione
- Separatrici, Separatrici, Metodi di Runge-Kutta, A.1 ESISTENZA E UNICITÀ, A.1 ESISTENZA E UNICITÀ, A.1 ESISTENZA E UNICITÀ
- controvariante
- Equazioni di Lagrange, Coordinate polari e forze , Caso integrabile, Integrali di lineaforme , Varietà differenziabili
- controvarianza
- Separatrici
- coordinate fisse con il corpo
- Isometrie
- coordinate lagrangiane
- Pendoli, Vincoli olonomi, Superfici di rivoluzione, Integrabilità
- coordinate polari
- Stabilità, Curve eccezionali, Coordinate polari e forze , Il problema nel piano
- coordinate polari sferiche
- Coordinate polari sferiche, Moti vincolati, Separazione di variabili, Gli integrali classici, Variabili di Delaunay
- corpo con simmetria sferica
- Satelliti artificiali
- corpo puntiforme
- Moti vincolati, Moti vincolati, Parametrizzazione delle orbite periodiche, Vincoli olonomi, Integrali primi del problema , Superfici di rivoluzione, 7.1 PROBLEMA DEI DUE , Isometrie
- corpo rigido
- Vincoli olonomi, Isometrie, Caso continuo, Integrabilità
- corpo rigido libero
- Integrabilità
- corrispondono per valore
- Le mappe che conservano , Le mappe che conservano , Equazioni di Lagrange, Trasformazioni canoniche, Momento angolare
- costante di Gauss
- Costanti ed unità di
- costante di gravitazione universale
- Costanti ed unità di , Costanti ed unità di
- costante di Lipschitz
- A.1 ESISTENZA E UNICITÀ
- costante solare
- Razzi e missili
- covariante
- Equazioni di Lagrange, Simmetrie nei sistemi lagrangiani, 6.5 SISTEMI HAMILTONIANI, Funzione generatrice, Integrali di lineaforme , Integrali di lineaforme , Forme differenziali
- criterio della traccia
- Le mappe che conservano , Equazioni lineari a coefficienti
- curva aperta
- Studio qualitativo
- curva eccezionale
- Nodi e selle, Nodi e selle, Nodi e selle, Nodi impropri, Sistemi con dissipazione, Curve eccezionali
- curva regolare
- Integrali di lineaforme
- curva regolare a tratti
- Funzioni generatrici, Integrali di lineaforme
- densità
- Caso continuo
- derivata totale
- Derivate, Derivata totale, Sistemi hamiltoniani, Equazioni di Newton
- diagonale a blocchi
- Sistema semisemplice, Un solo autovalore reale, Soluzione di un sistema , Caso lineare
- diagonalizzabile
- Diagonalizzazione, Equazioni lineari alle differenze , Le mappe che conservano
- diffeomorfismo
- 1.1 SISTEMI CONTINUI E , Equazione di Lagrange
- differenza all'indietro
- Discretizzazione di ordine superiore, Mappa standard
- differenza centrale
- Differenze centrali
- differenza in avanti
- Discretizzazione di ordine superiore
- differenza k-esima in avanti
- Discretizzazione di ordine superiore
- differenziabile
- Calcolo differenziale in più
- differenziazione esterna
- Funzione generatrice, Forme differenziali
- dimensione
- Pendoli, Varietà differenziabili
- dimensione infinita
- Quasipolinomi, A.1 ESISTENZA E UNICITÀ
- dinamiche equivalenti
- Equazione di Lagrange, Cambiamento di coordinata, Corpi non puntiformi, Le mappe che conservano , Equazioni di Newton, Equazioni di Lagrange, Equazioni di Lagrange, Trasformazione di Legendre, Riduzione alla forza centrale
- diofantea
- Soluzione per serie
- dipendenza critica dalla condizione iniziale
- Caso integrabile, Definizioni di caos
- direzione di fuga
- Satelliti artificiali
- discretizzazione
- Dimensione 1, Uso della forma canonica
- discriminante
- Dimensione 2, Oscillatori lineari
- diseguaglianza di Cauchy
- Norme di matrici, Caso nonlineare
- distanza angolare
- Razzi e missili, Razzi e missili
- divisore
- Soluzione per serie, 9.3 NON INTEGRABILITÀ SECONDO
- dominio di Delaunay
- Variabili di Delaunay
- doppia quadratura
- Perturbazioni
- eccentricità
- Scelta delle notazioni, Problema dei due corpi , Elementi orbitali
- effemeridi
- Orbite interplanetarie
- elementi orbitali
- Elementi orbitali, Parametrizzare una rotazione
- elevazione
- Satelliti artificiali
- elica cilindrica
- Moti vincolati - esempi, Soluzioni del capitolo 6
- ellissoide d'inerzia
- Equazioni di Eulero
- energia
- Il metodo della funzione , Equazioni di Newton
- energia cinetica
- Sistemi conservativi ad un , Esempi di sistemi hamiltoniani, Moti vincolati, Equazioni di Newton, Momento angolare, Energia cinetica e momento , Caso continuo
- energia potenziale
- Sistemi conservativi ad un , Esempi di sistemi hamiltoniani, Equazioni di Newton, 7.1 PROBLEMA DEI DUE
- energia potenziale effettiva
- Coordinate polari e forze , Il problema nel piano , Rotore simmetrico
- energia ridotta
- Gli integrali classici
- energia totale
- Equazioni di Newton, Sistemi hamiltoniani provenienti da , Gli integrali classici
- equazione alle differenze finite di ordine
- Equazioni alle differenze di , Equazioni alle differenze di
- equazione alle variazioni
- Separatrici, 8.6 EQUAZIONI ALLE VARIAZIONI, Flussi canonici, Definizione generale, A.4 DIFFERENZIABILITÀ
- equazione caratteristica
- Dimensione 2, Forma matriciale dei numeri , Sistema semisemplice, Oscillatori lineari, Ordine n, Caso nonlineare, Linearizzazione conservativa
- equazione del prezzo
- Esempi di modelli economici
- equazione del razzo
- Razzi e missili
- equazione della domanda
- Esempi di modelli economici
- equazione della produzione
- Esempi di modelli economici
- equazione delle scorte
- Esempi di modelli economici
- equazione di equilibrio del mercato
- Esempi di modelli economici , Esempi di modelli economici
- equazione di Hamilton-Jacobi
- Metodo di Hamilton-Jacobi, Variabili di Delaunay
- equazione di Keplero
- Orbite interplanetarie, Razzi e missili
- equazione di Lagrange
- Equazione di Lagrange, Equazione di Lagrange, Moti vincolati
- equazione di Lienard
- Il metodo della funzione
- equazione di Van der Pol
- Caso nonlineare
- equazione differenziale lineare
- 2.6 EQUAZIONI DI ORDINE , Oscillatori lineari, Ordine n, Ordine n, Ordine n, Equazioni alle differenze di , Equazioni alle differenze di
- equazioni di Eulero
- Equazioni di Eulero
- equazioni di Hamilton
- Sistemi hamiltoniani, Trasformata di Legendre, Trasformazione di Legendre, 6.5 SISTEMI HAMILTONIANI, Parametrizzare una rotazione, Flussi canonici, Caso integrabile
- equazioni di Lagrange
- Equazioni di Lagrange, Sistemi lagrangiani provenienti da , 7.1 PROBLEMA DEI DUE , Parametrizzare una rotazione, Flussi canonici
- equazioni perturbative
- Perturbazioni
- errore di troncamento accumulato
- Metodo di Eulero nel , Convergenza del metodo di , Esponenti di Lyapounov e
- errore di troncamento locale
- Metodo di Eulero nel , Convergenza del metodo di , Esponenti di Lyapounov e
- esplicito
- Metodi di Runge-Kutta
- esponenti di Lyapounov
- Esponenti di Lyapounov, Caso nonlineare, Punti stazionari ed hessiani, Selle in dimensione 2, Uso della forma canonica , Linearizzazione conservativa, Linearizzazione di sistemi newtoniani, 8.6 EQUAZIONI ALLE VARIAZIONI, Definizione generale, Definizione generale, Definizioni di caos
- esponenziale di matrice
- Dimensione n, Convergenza dell'esponenziale, Cambiamenti di coordinate, Un solo autovalore reale, Soluzione di un sistema , Isometrie, A.1 ESISTENZA E UNICITÀ
- esterno
- 3.8 TEOREMA DI POINCARÉ-BENDIXON, Topologia in
- fibrato tangente
- 1.1 SISTEMI CONTINUI E , Varietà differenziabili
- figure di Lissajous
- Oscillazioni proprie
- filo inestendibile pesante
- Forze non differenziabili
- finestra di lancio
- Orbite interplanetarie
- flusso di Kronecker
- Insiemi limite più complessi, Moti vincolati, Due gradi di libertà, Gli integrali classici, Oscillazioni proprie, Oscillazioni proprie, Caso integrabile, Soluzione per serie
- flusso integrale
- Sistemi lineari, Sistemi nonlineari, Dimensione 2, Soluzione di un sistema , Punti di equilibrio, I sistemi hamiltoniani sono , Simmetrie nei sistemi lagrangiani
- flusso integrale del sistema non autonomo
- 8.1 OMOGENEIZZAZIONE, A.1 ESISTENZA E UNICITÀ
- forma canonica del nilpotente
- Un solo autovalore reale, Oscillatori lineari, Caso lineare, Uso della forma canonica
- forma canonica di Jordan
- Un solo autovalore reale, Soluzione di un sistema , Soluzione di un sistema , Caso lineare, Sistemi a secondo membro , Forme canoniche
- forma canonica di Jordan reale
- Soluzione di un sistema , Soluzione di un sistema , Caso lineare, Uso della forma canonica , Linearizzazione conservativa, Forme canoniche
- forma canonica di un semisemplice
- Sistema semisemplice, Soluzione di un sistema
- forma chiusa
- Funzioni generatrici, Funzioni generatrici, Funzione generatrice, Funzione generatrice, Integrali di lineaforme , Forme differenziali
- forma differenziale lineare
- Funzioni generatrici, Funzione generatrice, Due gradi di libertà, Integrali di lineaforme
- forma differenziale quadratica
- Funzione generatrice, Forme differenziali
- forma esatta
- Funzioni generatrici, Funzione generatrice, Integrali di lineaforme , Forme differenziali
- forme differenziali lineari
- Forme differenziali
- formula della traccia
- Simmetrie nei sistemi lagrangiani, Isometrie, Wronskiano
- formula di Eulero
- Sistemi dinamici lineari complessi
- formula di Gauss
- Satelliti artificiali, Campi solenoidali
- formula di Green
- Funzioni generatrici, Variabile azione ed area, Integrali di lineaforme
- fortemente stabile
- Equazioni lineari a coefficienti
- forza apparente centrifuga
- Coordinate polari e forze , Sistemi di riferimento rotanti
- forza apparente di Coriolis
- Sistemi di riferimento rotanti
- forza centrale
- Coordinate polari e forze , Coordinate polari sferiche, Integrali primi del problema , Separazione di variabili, Separazione di variabili, 7.1 PROBLEMA DEI DUE , Riduzione alla forza centrale, Il problema nel piano
- frequenza propria
- Parametrizzazione delle orbite periodiche, Due gradi di libertà, N gradi di libertà, Gli integrali classici, Problema dei due corpi , Variabili di Delaunay, Oscillazioni proprie, Caso integrabile, Perturbazioni
- frontiera
- Il metodo della funzione , Integrali di lineaforme , Topologia in
- funzionalmente dipendenti
- 9.3 NON INTEGRABILITÀ SECONDO , Calcolo differenziale in più
- funzionalmente indipendenti
- Vincoli olonomi, Due gradi di libertà, N gradi di libertà, Calcolo differenziale in più
- funzione caratteristica di Hamilton-Jacobi
- Metodo di Hamilton-Jacobi, Separazione di variabili, Due gradi di libertà
- funzione di Lyapounov
- Caso nonlineare, Il metodo della funzione , Sistemi conservativi ad un , Sistemi con dissipazione, 3.7 INSIEMI LIMITE, Linearizzazione conservativa
- funzione di Lyapounov stretta
- Il metodo della funzione , Sistemi con dissipazione, Sistemi con dissipazione, Il potenziale come funzione
- funzione generatrice
- Funzioni generatrici, Funzione generatrice, Funzione generatrice, Funzione generatrice, Funzione generatrice, Metodo di Hamilton-Jacobi, Separazione di variabili
- funzione generatrice dipendente dal tempo
- Trasformazioni canoniche dipendenti dal
- funzione polidroma
- Funzione generatrice, Integrali di lineaforme
- fuoco
- Centri e fuochi, Punti di equilibrio, Stabilità, Caso lineare
- geodetiche
- Superfici di rivoluzione
- gradi di libertà
- 6.1 SISTEMI NEWTONIANI E , 6.5 SISTEMI HAMILTONIANI
- gradiente come vettore colonna
- Derivate, 3.5 GRADIENTI
- gruppo ad un parametro
- 3.7 INSIEMI LIMITE, Simmetrie nei sistemi lagrangiani, Due gradi di libertà
- gruppo ad un parametro di simmetrie
- Simmetrie nei sistemi lagrangiani
- gruppo continuo locale ad un parametro
- A.2 CONTINUAZIONE DELLE SOLUZIONI
- hamiltoniana
- Sistemi hamiltoniani, 6.5 SISTEMI HAMILTONIANI
- hamiltoniana omogenea
- Sistemi hamiltoniani dipendenti dal
- hessiana
- Calcolo differenziale in più
- identità
- Discretizzazione di ordine superiore
- implicito
- Metodi di Runge-Kutta
- in commutazione
- N gradi di libertà, N gradi di libertà, Rotore simmetrico, Oscillazioni proprie
- in;tex2html_html_special_mark_quot;commutazione
- Integrabilità
- inclinazione
- Elementi orbitali
- induttanza
- Circuiti elettrici lineari
- infinito
- Sistemi lineari, Nodi e selle, Topologia in
- insieme
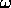 -limite
-limite - 3.7 INSIEMI LIMITE
- insieme
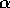 -limite
-limite - 3.7 INSIEMI LIMITE
- insieme
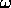 -limite
-limite - Orbite periodiche
- insieme
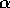 -limite
-limite - Orbite periodiche
- insieme
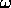 -limite
-limite - Caso non newtoniano
- insiemi limite
- 3.7 INSIEMI LIMITE, Studio qualitativo
- instabile
- Stabilità, Instabilità, Caso lineare, Caso nonlineare, Sistemi conservativi ad un , Linearizzazione conservativa
- integrabile
- Sistemi lineari, Sistemi conservativi ad un , 4.3 DISCRETIZZAZIONE CONSERVATIVA, 5.2 INTEGRABILITÀ, N gradi di libertà, 7.1 PROBLEMA DEI DUE , Integrabilità, Rotore simmetrico, Oscillazioni proprie, Caso integrabile, Perturbazioni, Integrabilità secondo Weierstrass
- integrabile secondo Weierstrass
- Integrabilità secondo Weierstrass
- integrale dell'energia
- Sistemi conservativi ad un , Mappa standard, Mappa standard, Equazioni di Newton
- integrale di linea
- Funzioni generatrici, Due gradi di libertà, Integrali di lineaforme
- integrale doppio
- Funzioni generatrici, Calcolo integrale in più
- integrale multiplo
- Calcolo integrale in più
- integrale primo
- Caso continuo, Caso discreto, Centri e fuochi, Sistemi conservativi ad un , Differenze centrali, Sistemi hamiltoniani, Parametrizzazione delle orbite periodiche, Equazioni di Newton, Due gradi di libertà, 7.1 PROBLEMA DEI DUE , Mappa di Poincaré
- integrale triplo
- Calcolo integrale in più
- integrazione di Riemann
- Caso continuo, Calcolo integrale in più
- interno
- 3.8 TEOREMA DI POINCARÉ-BENDIXON, Topologia in
- intervallo massimale
- A.2 CONTINUAZIONE DELLE SOLUZIONI
- invariante
- Caso continuo, Stabilità, Sistemi con dissipazione, Separatrici, Separatrici, 3.7 INSIEMI LIMITE, Due gradi di libertà, Momento angolare
- invarianti
- Diagonalizzazione, Sistema semisemplice, Polinomio caratteristico
- iperboloide a due falde
- Superfici di rivoluzione
- iperboloide ad una falda
- Superfici di rivoluzione
- ipersuperficie
- Mappa di Poincaré
- isole di risonanza
- Esempi di caos
- isometria
- Integrali primi del problema , Isometrie
- lagrangiana
- Esempi di sistemi hamiltoniani, Trasformata di Legendre, Moti vincolati, Equazioni di Lagrange, Sistemi lagrangiani provenienti da , 7.1 PROBLEMA DEI DUE , Riduzione alla forza centrale, Il problema nel piano , Caso continuo, Integrabilità, Parametrizzare una rotazione, Parametrizzare una rotazione, Linearizzazione di sistemi newtoniani, Linearizzazione di sistemi newtoniani, Oscillazioni proprie
- lancio di un missile intercontinentale
- Razzi e missili
- lancio di un satellite artificiale
- Satelliti artificiali
- lancio interplanetario
- Satelliti artificiali
- legge delle aree
- Il problema nel piano
- legge di Archimede
- Forze non differenziabili
- legge di azione e reazione
- Integrali primi del problema , 7.1 PROBLEMA DEI DUE
- legge oraria
- Nodi e selle, Legge oraria
- librazione
- Parametrizzazione delle orbite periodiche
- linea dei nodi
- Parametrizzare una rotazione
- lineare
- Sistemi lineari, Caso discreto, Dimensione n, Cambiamenti di coordinate, Soluzione di un sistema , 2.6 EQUAZIONI DI ORDINE , Caso lineare, Equazioni lineari alle differenze , Equazioni alle differenze di
- lineare non omogeneo
- Caso lineare
- lineare omogeneo
- Caso lineare
- linearizzati di sistemi hamiltoniani
- Linearizzazione conservativa, Caso integrabile
- linearizzato
- Esponenti di Lyapounov, Caso nonlineare, Caso nonlineare, Caso nonlineare, Sistemi conservativi ad un , Selle in dimensione 2, Separatrici, Linearizzazione conservativa
- linearmente stabile
- Linearizzazione conservativa
- lipschitziana
- Separatrici, Convergenza del metodo di , Forze non differenziabili, Esponenti di Lyapounov e , A.1 ESISTENZA E UNICITÀ
- localmente lipschitziana
- A.1 ESISTENZA E UNICITÀ
- longitudine del nodo
- Elementi orbitali
- lunghezza della curva
- Pendoli, Lunghezza di una curva
- mappa di Poincaré
- Mappa di Poincaré
- mappa standard
- Mappa standard, Parametrizzazione delle orbite periodiche, Esempi di caos
- mappa standard del pendolo
- Mappa standard, Metodi simplettici a scorrimento, Esempi di caos
- mappa standard del problema dei due corpi
- Mappa standard
- massa
- Sistemi conservativi ad un , Esempi di sistemi hamiltoniani, Equazione di Lagrange, Equazioni di Newton
- massa ridotta
- Riduzione alla forza centrale
- massa totale
- Caso continuo
- matrice compagna
- Ordine n, Ordine n, Ordine n, Equazioni alle differenze di
- matrice di monodromia
- 8.6 EQUAZIONI ALLE VARIAZIONI, Definizione generale
- matrice di Vandermonde
- Metodi di Runge-Kutta
- matrice semisemplice
- Sistema semisemplice, Soluzione di un sistema , Caso lineare, Equazioni lineari alle differenze , Forme canoniche
- matrice simplettica
- Le mappe che conservano , Trasformazioni canoniche, Flussi canonici, Caso integrabile
- matrici simplettiche iperboliche
- Le mappe che conservano
- matrici simplettiche stabili
- Le mappe che conservano
- media armonica
- Riduzione alla forza centrale
- metodi simplettici a scorrimento
- Metodi simplettici a scorrimento, Esempi di sistemi hamiltoniani
- metodo di Eulero
- Metodo di Eulero nel , Convergenza del metodo di , Esponenti di Lyapounov e
- metodo di integrazione simplettico
- Metodi simplettici a scorrimento, Metodi di Runge-Kutta, Metodi di Runge-Kutta
- metodo di Newton
- Orbite interplanetarie
- metodo di Runge-Kutta
- Metodi di Runge-Kutta
- metodo di Runge-Kutta classico
- Metodi di Runge-Kutta
- metodo di Runge-Kutta-Gauss
- Metodi di Runge-Kutta, Metodi di Runge-Kutta
- metrica della convergenza uniforme
- Separatrici, A.1 ESISTENZA E UNICITÀ, A.1 ESISTENZA E UNICITÀ, B.4 SERIE DI FUNZIONI
- minimo limite
- 3.7 INSIEMI LIMITE
- minimo locale forte
- Il potenziale come funzione , Linearizzazione conservativa, Calcolo differenziale in più
- minimo;tex2html_html_special_mark_quot;limite
- Topologia in
- missili balistici
- Razzi e missili
- misurabile secondo Peano-Jordan
- Caso continuo, Calcolo integrale in più
- modello della ragnatela
- Esempi di modelli economici
- modello delle scorte
- Esempi di modelli economici
- molteplicità algebrica
- Dimensione 2, Sistema semisemplice, Soluzione di un sistema , Soluzione di un sistema , Soluzione di un sistema , Soluzione di un sistema , Oscillatori lineari, Ordine n, Caso lineare, Polinomio caratteristico
- molteplicità dell'autovalore
- Un solo autovalore reale, Soluzione di un sistema , Ordine n, Trasformazioni canoniche, Polinomio caratteristico
- moltiplicatori di Lagrange
- Vincoli olonomi
- moltiplicatori di Lyapounov
- Uso della forma canonica , Esempi di modelli economici
- momenti coniugati
- Equazioni di Lagrange, Trasformazione di Legendre, Variabili cicliche, 6.5 SISTEMI HAMILTONIANI
- momenti principali d'inerzia
- Energia cinetica e momento , Equazioni di Eulero
- momento
- Esempi di sistemi hamiltoniani, Legge oraria, Trasformata di Legendre
- momento angolare
- Integrali primi del problema , Separazione di variabili, Separazione di variabili, N gradi di libertà, Momento angolare, Energia cinetica e momento , Caso continuo, Integrabilità, Integrabilità
- momento d'inerzia
- Corpi non puntiformi, Vincoli olonomi, Moti vincolati, Energia cinetica e momento , Caso continuo
- moto alla Poinsot
- Equazioni di Eulero
- moto medio
- Problema dei due corpi , Variabili di Delaunay, Orbite interplanetarie
- moto relativistico
- Esempi non strettamente meccanici
- moto vincolato
- Esempi di sistemi hamiltoniani, Moti vincolati, Vincoli olonomi, Varietà differenziabili
- movimento rigido
- Isometrie
- multiindice
- Soluzione per serie, B.4 SERIE DI FUNZIONI
- muro di potenziale
- Variabile azione ed area, Variabile azione ed area
- nilpotente
- Esempi, Un solo autovalore reale, Soluzione di un sistema , Ordine n, Ordine n, Equazioni lineari alle differenze , Forme canoniche, Forme canoniche
- nodo
- Nodi e selle, Punti di equilibrio, Caso lineare, Curve eccezionali
- nodo ascendente
- Elementi orbitali, Parametrizzare una rotazione
- nodo improprio
- Nodi impropri, Caso lineare
- non autonomo
- 8.1 OMOGENEIZZAZIONE
- non degenerazione
- Trasformazione di Legendre, Trasformazione di Legendre
- non degenere
- 9.3 NON INTEGRABILITÀ SECONDO
- non integrabile
- Instabilità, Due gradi di libertà, Rotore simmetrico, Esponenti di Lyapounov e , Integrabilità secondo Weierstrass
- non omogenea
- 2.6 EQUAZIONI DI ORDINE , Ordine n, Equazioni alle differenze di , Esempi di modelli economici , Convergenza del metodo di , Equazioni differenziali di ordine
- nonlineare
- Sistemi nonlineari, Convergenza del metodo di
- norma
- Norme di matrici, Caso lineare, Topologia in , B.4 SERIE DI FUNZIONI
- norma del massimo
- Norme di matrici
- norma euclidea
- Norme di matrici, Caso nonlineare
- norma uniforme
- Norme di matrici, Metodo di Eulero nel , Caso integrabile
- Numeri di Fibonacci
- Equazioni alle differenze di
- omeomorfismo
- Separatrici, Topologia in , Varietà differenziabili
- omogenea
- 2.6 EQUAZIONI DI ORDINE , Oscillatori lineari, Ordine n, Ordine n, 8.2 EQUAZIONI LINEARI NON
- omogeneizzazione
- Equazioni alle differenze di , Metodi di Runge-Kutta, Sistemi hamiltoniani dipendenti dal , 8.1 OMOGENEIZZAZIONE
- operatore d'inerzia
- Energia cinetica e momento , Caso continuo
- operatori differenziali
- Ordine n
- orbita
- 1.1 SISTEMI CONTINUI E , 1.1 SISTEMI CONTINUI E , Punti di equilibrio, 3.7 INSIEMI LIMITE, Definizione generale
- orbita caotica
- Definizioni di caos
- orbita di trasferimento di Hohmann
- Satelliti artificiali, Orbite interplanetarie, Orbite interplanetarie
- orbita periodica
- Centri e fuochi, Orbite periodiche, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Orbite periodiche, Caso non newtoniano, Problema dei due corpi , Definizione generale
- ordine
- Caso continuo, 2.6 EQUAZIONI DI ORDINE , Oscillatori lineari, Ordine n, Ordine n, Sistemi conservativi ad un , Equazioni alle differenze di
- ordine del nilpotente
- Un solo autovalore reale, Soluzione di un sistema , Ordine n
- ordine di troncamento
- Metodi simplettici a scorrimento, Metodi di Runge-Kutta, Metodi di Runge-Kutta
- oscillatore armonico
- Caso continuo, Sistemi dinamici lineari complessi, Centri e fuochi, Risonanza, Metodo di Eulero nel , Discretizzazione di ordine superiore, Differenze centrali, Esempi di sistemi hamiltoniani, Funzioni generatrici, Parametrizzazione delle orbite periodiche, Funzione generatrice, Metodo di Hamilton-Jacobi, Equazioni di Eulero, Oscillazioni proprie
- oscillatore armonico forzato
- Esempi di sistemi hamiltoniani, Ampiezze complesse
- oscillatore lineare
- Oscillatori lineari, Circuiti elettrici lineari, Ordine n, Ampiezze complesse, Soluzioni del capitolo 2
- oscillatore lineare forzato
- Ampiezze complesse
- oscillatore lineare smorzato
- Ampiezze complesse
- oscillazione propria
- Oscillazioni proprie
- oscillazione smorzata
- Oscillatori lineari, Circuiti elettrici lineari, Sistemi con dissipazione
- parametro arco
- Pendoli, Lunghezza di una curva
- parentesi di Poisson
- Sistemi hamiltoniani, Due gradi di libertà, N gradi di libertà, 9.3 NON INTEGRABILITÀ SECONDO
- partizione
- Caso continuo, Calcolo integrale in più
- passo d'integrazione
- Dimensione 1, Uso della forma canonica , Metodo di Eulero nel , Metodi di Runge-Kutta
- pendolo
- Caso lineare, Sistemi conservativi ad un , Mappa standard, Metodi simplettici a scorrimento, Metodi di Runge-Kutta, Pendoli, Parametrizzazione delle orbite periodiche
- pendolo cicloidale
- Pendoli
- pendolo doppio
- Moti vincolati, Simmetrie nei sistemi lagrangiani, Oscillazioni proprie
- pendolo lineare con dissipazione
- Caso lineare
- pendolo nonlineare con dissipazione
- Caso nonlineare, Sistemi con dissipazione, Separatrici
- pendolo sferico
- Moti vincolati, Superfici di rivoluzione
- pericentro
- Gli integrali classici, Problema dei due corpi
- perielio
- Orbite interplanetarie
- perigeo
- Satelliti artificiali
- periodo
- Orbite periodiche, Orbite periodiche, Sistemi periodici
- periodo sinodico
- Orbite interplanetarie
- perturbazione
- Perturbazioni
- piano di Argand-Gauss
- Forma matriciale dei numeri
- piano inclinato
- Corpi non puntiformi
- poligono di Eulero
- Metodo di Eulero nel , Convergenza del metodo di
- polinomio caratteristico
- Dimensione 2, Trasformazioni canoniche, Polinomio caratteristico
- positivamente invariante
- Sistemi con dissipazione, 3.7 INSIEMI LIMITE
- potenziale
- 3.5 GRADIENTI
- pozzo
- Esponenti di Lyapounov, Caso nonlineare, Il metodo della funzione , Punti stazionari ed hessiani, Selle in dimensione 2
- prima forma fondamentale
- Varietà differenziabili
- prima legge di Keplero
- Problema dei due corpi
- prima velocità cosmica
- Satelliti artificiali, Costanti ed unità di , Razzi e missili
- principio di sovrapposizione
- Integrali primi del problema
- principio variazionale
- Superfici di rivoluzione
- problema degli n corpi
- Integrali primi del problema , Integrabilità
- problema dei due corpi
- Mappa standard, 7.1 PROBLEMA DEI DUE , Soluzione per serie
- prodotto triplo
- Energia cinetica e momento
- proviene da un sistema newtoniano
- Sistemi lagrangiani provenienti da , Linearizzazione di sistemi newtoniani
- punto di equilibrio
- Centri e fuochi
- punto di equilibrio
- Nodi e selle, Nodi e selle, Nodi e selle, Nodi impropri, Punti di equilibrio, Orbite periodiche, Linearizzazione conservativa
- punto di equilibrio degenere
- Curve eccezionali
- punto limite
- Punti di equilibrio
- quadratura
- Sistemi nonlineari, Legge oraria, Variabili cicliche, Moti vincolati, Metodo di Hamilton-Jacobi, Due gradi di libertà, Il problema nel piano , Gli integrali classici, Orbite interplanetarie, Rotore simmetrico, Rotore simmetrico, Perturbazioni
- quantità di moto
- Integrali primi del problema , Riduzione alla forza centrale
- quasipolinomi
- Ordine n, Ordine n, Quasipolinomi, Ampiezze complesse, 8.3 SISTEMI LINEARI NON , Sistemi a secondo membro
- rapporto di massa
- Razzi e missili
- rappresentazione algebrica del numero complesso
- Forma matriciale dei numeri
- rappresentazione cartesiana del numero complesso
- Forma matriciale dei numeri
- rappresentazione matriciale del numero complesso
- Forma matriciale dei numeri
- reazioni vincolari
- Moti vincolati, Vincoli olonomi, Moti vincolati, Varietà differenziabili
- regione caotica
- Definizioni di caos
- regola dell'elettrotecnico
- Sistemi a secondo membro , Circuiti accoppiati
- regola della velocità angolare
- Integrali primi del problema , Sistemi di riferimento rotanti, Isometrie, Equazioni di Eulero, Parametrizzare una rotazione
- resistenza
- Circuiti elettrici lineari
- reversibile
- Metodi simplettici a scorrimento
- risonanza
- Risonanza, Mappa standard, Ampiezze complesse, Ampiezze complesse, Soluzione per serie
- risonanza parametrica
- Equazioni lineari a coefficienti
- rotazione
- Isometrie
- rotore
- Equazioni di Newton, Integrali di lineaforme
- rotore libero
- Parametrizzazione delle orbite periodiche, Moti vincolati
- rotore simmetrico
- Rotore simmetrico
- scorrimento
- Caso discreto, Nodi impropri, Mappa standard, Metodi simplettici a scorrimento, Esempi di sistemi hamiltoniani, Le mappe che conservano , Funzioni generatrici, Due gradi di libertà, Perturbazioni
- seconda forma fondamentale
- Vincoli olonomi, Varietà differenziabili
- seconda legge di Keplero
- Il problema nel piano
- seconda velocità cosmica
- Satelliti artificiali
- secondo stadio
- Razzi e missili
- sella
- Nodi e selle, Instabilità, Caso nonlineare, Sistemi con dissipazione, Punti stazionari ed hessiani, Selle in dimensione 2, Linearizzazione di sistemi newtoniani
- sella nonlineare
- Sistemi con dissipazione, Selle in dimensione 2, Curve eccezionali, Soluzioni del capitolo 3
- semiasse maggiore
- Problema dei due corpi
- separatrice
- Sistemi conservativi ad un , Separatrici, Mappa standard, Forze non differenziabili, Esempi di caos
- separazione delle variabili
- Separazione di variabili, Due gradi di libertà
- sequenza monotona
- 3.8 TEOREMA DI POINCARÉ-BENDIXON, 3.8 TEOREMA DI POINCARÉ-BENDIXON, 3.8 TEOREMA DI POINCARÉ-BENDIXON
- serie di Fourier
- Soluzione per serie, B.4 SERIE DI FUNZIONI
- serie di potenze
- B.4 SERIE DI FUNZIONI
- serie prodotto secondo Cauchy
- Serie prodotto, B.4 SERIE DI FUNZIONI
- sezione locale
- 3.8 TEOREMA DI POINCARÉ-BENDIXON, Caso non newtoniano, Mappa di Poincaré, Mappa di Poincaré
- simmetria assiale
- Equazioni di Eulero, Rotore simmetrico
- singolarità isolate
- Moti vincolati, Moti vincolati, Oscillazioni proprie
- sistema dinamico continuo
- 1.1 SISTEMI CONTINUI E , Dimensione 1, Sistemi lineari, 2.6 EQUAZIONI DI ORDINE , 3.1 STABILITÀ
- sistema dinamico discreto
- 1.1 SISTEMI CONTINUI E , Dimensione 1, Equazioni lineari alle differenze
- sistema dinamico discreto conservativo
- Caso discreto, Mappa standard, Mappa standard, Le mappe che conservano , Mappa di Poincaré
- sistema dinamico gradiente
- 3.5 GRADIENTI
- sistema dissipativo ad un grado di libertà
- Sistemi con dissipazione, Sistemi con dissipazione
- sistema fondamentale di intorni
- Stabilità, Il metodo della funzione , Topologia in
- sistema fondamentale di soluzioni
- Caso lineare, Wronskiano, 8.6 EQUAZIONI ALLE VARIAZIONI, Flussi canonici, A.4 DIFFERENZIABILITÀ
- sistema hamiltoniano
- Metodi di Runge-Kutta, 6.5 SISTEMI HAMILTONIANI, Soluzioni del capitolo 3
- sistema hamiltoniano ad un grado di libertà
- Sistemi hamiltoniani
- sistema lagrangiano
- Equazioni di Lagrange
- sistema lineare non autonomo
- Wronskiano
- sistema newtoniano
- Equazioni di Newton
- sistema newtoniano ad un grado di libertà
- Sistemi conservativi ad un , Mappa standard, Metodi di Runge-Kutta, Sistemi newtoniani
- sistema newtoniano conservativo
- Equazioni di Newton, Flussi canonici
- sistema rigido
- Isometrie, Energia cinetica e momento
- sistemi inerziali
- Equazioni di Newton, Isometrie, Parametrizzare una rotazione
- solenoidale
- Satelliti artificiali, Campi solenoidali
- soluzione
- 1.1 SISTEMI CONTINUI E , 3.1 STABILITÀ, 3.7 INSIEMI LIMITE
- soluzione asintoticamente stabile
- Sistemi periodici
- soluzione generale
- Sistemi lineari
- soluzione particolare
- Caso lineare, 8.3 SISTEMI LINEARI NON , Sistemi a secondo membro
- soluzione stabile
- Sistemi periodici
- sorgente
- Esponenti di Lyapounov, Caso nonlineare, Punti stazionari ed hessiani, Selle in dimensione 2, Curve eccezionali
- sottogruppo di isotropia
- Due gradi di libertà
- sottovarietà
- Separatrici, Varietà differenziabili
- spazio affine
- Caso lineare
- spazio delle configurazioni
- Pendoli, 6.1 SISTEMI NEWTONIANI E , Equazioni di Lagrange, Vincoli olonomi, Moti vincolati, 6.5 SISTEMI HAMILTONIANI
- spazio delle fasi
- 6.1 SISTEMI NEWTONIANI E , Trasformazione di Legendre, 6.5 SISTEMI HAMILTONIANI
- spazio metrico completo
- Separatrici, A.1 ESISTENZA E UNICITÀ, B.4 SERIE DI FUNZIONI
- spazio tangente
- Vincoli olonomi, Varietà differenziabili
- spostamento
- Equazioni alle differenze di , Discretizzazione di ordine superiore
- stabile
- Stabilità, Caso lineare, Il metodo della funzione , Sistemi conservativi ad un , Linearizzazione conservativa
- stadio
- Satelliti artificiali
- struttura complessa
- Forma matriciale dei numeri , Trasformazioni canoniche
- struttura simplettica
- Trasformazioni canoniche, Funzione generatrice, Linearizzazione conservativa, Flussi canonici
- studio delle proprietà qualitative
- Studio qualitativo
- sublineare
- A.1 ESISTENZA E UNICITÀ
- successione di Cauchy
- A.1 ESISTENZA E UNICITÀ
- superficie di rivoluzione
- Superfici di rivoluzione
- tempo
- 1.1 SISTEMI CONTINUI E , 6.7 OMOGENEIZZAZIONE CONSERVATIVA, 8 EQUAZIONI DIFFERENZIALI DIPENDENTI
- tempo di Lyapounov
- Esponenti di Lyapounov e , Definizioni di caos
- tensore d'inerzia
- Energia cinetica e momento , Caso continuo, Trottola simmetrica
- Teorema abbassamento di grado dei quasipolinomi
- Equazioni differenziali di ordine , Ampiezze complesse, Soluzioni del capitolo 8
- Teorema Arnold-Jost
- Due gradi di libertà, Superfici di rivoluzione, N gradi di libertà, N gradi di libertà, 7.1 PROBLEMA DEI DUE , Gli integrali classici, Gli integrali classici, Variabili di Delaunay, Integrabilità, Oscillazioni proprie, Integrabilità secondo Weierstrass
- Teorema cambiamento di variabili negli integrali doppi
- Mappa standard, Calcolo integrale in più
- Teorema completezza delle funzioni continue
- Dimensione 1, Convergenza dell'esponenziale, A.1 ESISTENZA E UNICITÀ, B.4 SERIE DI FUNZIONI
- Teorema conseguenti
- Mappa di Poincaré
- Teorema continuazione delle soluzioni
- Punti di equilibrio, Caso nonlineare, Sistemi con dissipazione, Il potenziale come funzione , Separatrici, 3.7 INSIEMI LIMITE, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Caso non newtoniano, A.2 CONTINUAZIONE DELLE SOLUZIONI
- Teorema continuità del flusso
- Punti di equilibrio, Esponenti di Lyapounov e , Mappa di Poincaré, A.3 MAGGIORAZIONE DELLE SOLUZIONI, A.4 DIFFERENZIABILITÀ, A.4 DIFFERENZIABILITÀ
- Teorema convergenza del metodo di Eulero
- Metodo di Eulero nel , Convergenza del metodo di , Esponenti di Lyapounov e
- Teorema convergenza dell'esponenziale di matrici
- Convergenza dell'esponenziale
- Teorema convergenza in norma
- Convergenza dell'esponenziale, Sistemi dinamici lineari complessi, Sistemi dinamici lineari complessi, Metodo di Eulero nel , B.4 SERIE DI FUNZIONI
- Teorema covarianza dell'equazione di Lagrange
- Cambiamento di coordinata, Pendoli
- Teorema covarianza delle equazioni di Lagrange
- Equazioni di Lagrange, Moti vincolati, Riduzione alla forza centrale
- Teorema curva di Jordan
- 3.8 TEOREMA DI POINCARÉ-BENDIXON, 3.8 TEOREMA DI POINCARÉ-BENDIXON, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Topologia in
- Teorema curve di livello della hamiltoniana
- Caso non newtoniano
- Teorema decomposizione S + N
- Soluzione di un sistema , Risonanza, Uso della forma canonica , Forme canoniche
- Teorema derivate miste
- Derivate, Punti stazionari ed hessiani, Calcolo differenziale in più , Integrali di lineaforme , Forme differenziali
- Teorema derivazione dell'esponenziale
- Convergenza dell'esponenziale, Serie prodotto, Parametrizzare una rotazione
- Teorema derivazione per serie
- Convergenza dell'esponenziale, B.4 SERIE DI FUNZIONI
- Teorema derivazione sui quasipolinomi
- Quasipolinomi, Sistemi a secondo membro
- Teorema determinante wronskiano
- Wronskiano
- Teorema determinante;tex2html_html_special_mark_quot;wronskiano
- Sistemi periodici
- Teorema diagonalizzazione delle forme quadratiche
- Punti stazionari ed hessiani, Energia cinetica e momento , Forme canoniche
- Teorema diagonalizzazione simultanea
- Linearizzazione di sistemi newtoniani, Forme canoniche
- Teorema differenziabilità del flusso
- Punti di equilibrio, Separatrici, 3.8 TEOREMA DI POINCARÉ-BENDIXON, 8.6 EQUAZIONI ALLE VARIAZIONI, Definizione generale, Mappa di Poincaré, A.4 DIFFERENZIABILITÀ
- Teorema diseguaglianza di Gronwall
- Esponenti di Lyapounov e , A.1 ESISTENZA E UNICITÀ, A.3 MAGGIORAZIONE DELLE SOLUZIONI, A.3 MAGGIORAZIONE DELLE SOLUZIONI, A.3 MAGGIORAZIONE DELLE SOLUZIONI
- Teorema equivalenza delle norme
- Norme di matrici, Caso nonlineare, Caso nonlineare, Topologia in
- Teorema esistenza (caso lineare)
- Wronskiano, A.3 MAGGIORAZIONE DELLE SOLUZIONI
- Teorema esistenza delle curve eccezionali
- Curve eccezionali, Separatrici, Linearizzazione conservativa
- Teorema esistenza e unicità
- Ordine n, Punti di equilibrio, Punti di equilibrio, Forze non differenziabili, 8.1 OMOGENEIZZAZIONE, A.1 ESISTENZA E UNICITÀ, A.3 MAGGIORAZIONE DELLE SOLUZIONI
- Teorema esistenza e unicità delle separatrici
- Sistemi con dissipazione, Separatrici
- Teorema flusso canonico
- Flussi canonici, Caso integrabile, Mappa di Poincaré
- Teorema fondamentale dell'algebra
- Dimensione 2, Sistema semisemplice, Polinomio caratteristico
- Teorema forma canonica dei nilpotenti
- Un solo autovalore reale, Un solo autovalore reale, Soluzione di un sistema , Forme canoniche
- Teorema funzione di Lyapounov decrescente
- Il metodo della funzione , Sistemi con dissipazione, Sistemi con dissipazione, Sistemi con dissipazione, 3.7 INSIEMI LIMITE
- Teorema funzione generatrice
- Funzioni generatrici, Funzione generatrice
- Teorema funzione inversa
- Funzioni generatrici, Trasformazione di Legendre, Funzione generatrice, Calcolo differenziale in più
- Teorema funzioni implicite
- 3.5 GRADIENTI, Caso non newtoniano, Trasformazione di Legendre, Vincoli olonomi, Moti vincolati, Due gradi di libertà, Mappa di Poincaré, Calcolo differenziale in più , Varietà differenziabili
- Teorema Hamilton-Cayley
- Forma matriciale dei numeri , Polinomio caratteristico
- Teorema Hohmann
- Satelliti artificiali
- Teorema integrabilità delle funzioni continue
- Caso continuo, Calcolo integrale in più
- Teorema invarianza degli insiemi limite
- Il potenziale come funzione , 3.7 INSIEMI LIMITE, 3.8 TEOREMA DI POINCARÉ-BENDIXON
- Teorema isomorfismo tra quasipolinomi
- Equazioni differenziali di ordine , Equazioni differenziali di ordine , Ampiezze complesse, Soluzioni del capitolo 8
- Teorema Jordan
- Ordine n, Caso lineare, Forme canoniche
- Teorema lagrangiana del corpo rigido
- Parametrizzare una rotazione
- Teorema linearizzazione delle selle
- Separatrici
- Teorema Liouville
- Trasformazioni canoniche, Caso integrabile
- Teorema Liouville in due variabili
- I sistemi hamiltoniani sono
- Teorema mappa standard
- Mappa standard, Metodi simplettici a scorrimento
- Teorema metodi di Runge-Kutta conservativi
- Metodi di Runge-Kutta
- Teorema momento angolare
- Integrabilità, Momento angolare
- Teorema moti vincolati
- Moti vincolati, Moti vincolati, Caso continuo
- Teorema moto ordinato
- Caso integrabile
- Teorema Noether
- Simmetrie nei sistemi lagrangiani, Due gradi di libertà, Momento angolare, Variabili di Delaunay, Integrabilità, Integrabilità
- Teorema non integrabilità di Poincaré
- 9.3 NON INTEGRABILITÀ SECONDO
- Teorema norma adattata
- Caso lineare, Caso nonlineare
- Teorema operatore alle differenze finite lineare
- Equazioni alle differenze di
- Teorema operatore differenziale lineare
- Ordine n, Ordine n, Equazioni alle differenze di
- Teorema Poincaré
- Funzione generatrice, Funzione generatrice, Forme differenziali
- Teorema Poincaré-Bendixon
- 3.8 TEOREMA DI POINCARÉ-BENDIXON, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Caso non newtoniano
- Teorema pozzo lineare
- Caso lineare, Uso della forma canonica
- Teorema pozzo nonlineare
- Caso nonlineare, Caso nonlineare, Il metodo della funzione
- Teorema prodotto secondo Cauchy
- Serie prodotto, Serie prodotto, B.4 SERIE DI FUNZIONI
- Teorema punti limite di un sistema gradiente
- Il potenziale come funzione
- Teorema punto fisso
- 3.8 TEOREMA DI POINCARÉ-BENDIXON
- Teorema punto limite
- Punti di equilibrio
- Teorema punto unito
- Separatrici, Metodi di Runge-Kutta, A.1 ESISTENZA E UNICITÀ
- Teorema quantità di moto
- Integrabilità
- Teorema ritorno
- Oscillazioni proprie, 9.3 NON INTEGRABILITÀ SECONDO
- Teorema rotazioni di Eulero
- Integrali primi del problema , Isometrie, Isometrie, Caso continuo
- Teorema rotazioni infinitesimali
- Isometrie, Parametrizzare una rotazione
- Teorema sistema diagonalizzabile
- Diagonalizzazione
- Teorema sistema non omogeneo quasipolinomiale
- Sistemi a secondo membro
- Teorema sistema semisemplice
- Sistema semisemplice, Soluzione di un sistema , Caso lineare
- Teorema soluzioni del sistema dinamico lineare
- Soluzione di un sistema , Soluzione di un sistema , Soluzione di un sistema , Ordine n, Ordine n, Caso lineare
- Teorema soluzioni dell'equazione a coefficienti costanti
- Ordine n, Equazioni alle differenze di , Quasipolinomi, Quasipolinomi
- Teorema soluzioni dell'equazione alle differenze finite
- Equazioni alle differenze di
- Teorema soluzioni dell'equazione alle differenze prime
- Uso della forma canonica , Equazioni alle differenze di
- Teorema soluzioni periodiche
- Sistemi periodici, Equazioni lineari a coefficienti
- Teorema somma degli esponenti
- Serie prodotto, Centri e fuochi, Un solo autovalore reale, Nodi impropri, Soluzione di un sistema , Risonanza, Isometrie
- Teorema sorgente lineare
- Caso lineare
- Teorema sorgente nonlineare
- Caso nonlineare
- Teorema stabilità del minimo
- Sistemi conservativi ad un , Moti vincolati, Moti vincolati, Linearizzazione conservativa
- Teorema stabilità di Lyapounov
- Il metodo della funzione , Sistemi con dissipazione, Il potenziale come funzione , Moti vincolati, Linearizzazione conservativa
- Teorema Steiner
- Trottola simmetrica
- Teorema tensore d'inerzia
- Energia cinetica e momento
- Teorema trasformata di Legendre
- Trasformazione di Legendre
- Teorema trasformazioni canoniche
- Trasformazioni canoniche, Funzione generatrice
- Teorema trasformazioni che conservano l'area
- Le mappe che conservano , Trasformazioni canoniche, Flussi canonici
- terza legge di Keplero
- Mappa standard, Problema dei due corpi , Variabili di Delaunay, Satelliti artificiali, Costanti ed unità di , Costanti ed unità di
- terza velocità cosmica
- Costanti ed unità di , Costanti ed unità di
- toro
- Scelta delle notazioni, Insiemi limite più complessi, Moti vincolati, Due gradi di libertà, Superfici di rivoluzione, N gradi di libertà, Variabili di Delaunay, Caso integrabile
- traccia
- Dimensione 2, Polinomio caratteristico
- traiettoria
- Nodi e selle, 3.7 INSIEMI LIMITE, Orbite periodiche, Orbite periodiche
- trasformata di Legendre
- Trasformata di Legendre, Trasformazione di Legendre, Parametrizzare una rotazione, Rotore simmetrico
- trasformatore
- Circuiti accoppiati
- trasformazione canonica
- Metodi di Runge-Kutta, Le mappe che conservano , Parametrizzazione delle orbite periodiche, Trasformazioni canoniche, Mappa di Poincaré, Mappa di Poincaré
- trasformazione di Legendre
- Trasformata di Legendre, Trasformazione di Legendre, Flussi canonici
- trasformazione di Legendre inversa
- Trasformazione di Legendre
- traslazione
- Isometrie
- trasversalmente
- Sistemi con dissipazione, 3.8 TEOREMA DI POINCARÉ-BENDIXON, Orbite periodiche, Mappa di Poincaré
- trottola pesante
- Trottola simmetrica
- uniformemente continua
- A.1 ESISTENZA E UNICITÀ, A.3 MAGGIORAZIONE DELLE SOLUZIONI
- uniformemente convergente
- Dimensione 1, Metodo di Eulero nel , Soluzione per serie, Integrabilità secondo Weierstrass, B.4 SERIE DI FUNZIONI
- uniformemente lipschitziano
- A.1 ESISTENZA E UNICITÀ, A.2 CONTINUAZIONE DELLE SOLUZIONI, A.3 MAGGIORAZIONE DELLE SOLUZIONI
- unità astronomica
- Costanti ed unità di
- variabile angolo
- Stabilità, Sistemi con dissipazione, Insiemi limite più complessi, Mappa standard, Pendoli, Parametrizzazione delle orbite periodiche, Orbite interplanetarie, Parametrizzare una rotazione, Caso integrabile, Perturbazioni
- variabile azione
- Parametrizzazione delle orbite periodiche
- variabile ciclica
- Variabili cicliche, Coordinate polari e forze , Separazione di variabili, Rotore simmetrico
- variabili azione
- Due gradi di libertà, N gradi di libertà
- variabili azione-angolo
- Variabile azione ed area, Separazione di variabili, Superfici di rivoluzione, N gradi di libertà, Variabili di Delaunay, Orbite interplanetarie, Caso integrabile, Perturbazioni
- variabili di Delaunay
- Variabili di Delaunay
- variabili separabili
- Sistemi nonlineari, Legge oraria
- variazione delle costanti arbitrarie
- Variazione delle costanti arbitrarie, Sistemi a secondo membro
- varietà differenziabile
- 1.1 SISTEMI CONTINUI E , Pendoli, Vincoli olonomi, Due gradi di libertà, Varietà differenziabili
- varietà topologica
- Varietà differenziabili
- vela solare
- Razzi e missili, Razzi e missili
- velocità angolare
- Caso lineare, Caso nonlineare, Sistemi conservativi ad un , Pendoli, Isometrie, Caso continuo, Integrabilità
- velocità di fuga
- Satelliti artificiali, Costanti ed unità di
- velocità generalizzata
- Trasformata di Legendre, Equazioni di Lagrange, Trasformazione di Legendre
- vettore assiale
- Isometrie, Isometrie, Parametrizzare una rotazione, Parametrizzare una rotazione
- vettore di Laplace-Lenz
- Elementi orbitali, Orbite interplanetarie, Parametrizzare una rotazione
- vettore variazione
- Caso integrabile
- vincoli
- Sistemi lagrangiani provenienti da , Vincoli olonomi
- vincoli lisci
- Vincoli olonomi, Moti vincolati
- vincoli olonomi
- Vincoli olonomi, Moti vincolati
- wronskiano
- Wronskiano
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
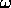 -limite
-limite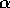 -limite
-limite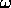 -limite
-limite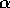 -limite
-limite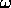 -limite
-limite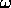 -limite
-limite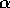 -limite
-limite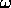 -limite
-limite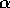 -limite
-limite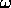 -limite
-limite