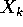 approssimano la
soluzione del sistema dinamico continuo su una successione di
tempi, per esempio
approssimano la
soluzione del sistema dinamico continuo su una successione di
tempi, per esempio 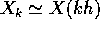 . Esistono moltissimi metodi di
integrazione numerica, e qui ne presentiamo soltanto alcuni,
commentando i rispettivi vantaggi e svantaggi.
. Esistono moltissimi metodi di
integrazione numerica, e qui ne presentiamo soltanto alcuni,
commentando i rispettivi vantaggi e svantaggi.
Sommario Quando un sistema dinamico non è integrabile mediante
un'espressione analitica esplicita, il che si verifica nella
stragrande maggioranza dei casi, può essere necessario usare un
procedimento che fornisca un'approssimazione della soluzione. Un
metodo di integrazione numerica è quindi un algoritmo che definisce
un sistema dinamico discreto le cui soluzioni 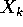 approssimano la
soluzione del sistema dinamico continuo su una successione di
tempi, per esempio
approssimano la
soluzione del sistema dinamico continuo su una successione di
tempi, per esempio 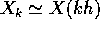 . Esistono moltissimi metodi di
integrazione numerica, e qui ne presentiamo soltanto alcuni,
commentando i rispettivi vantaggi e svantaggi.
. Esistono moltissimi metodi di
integrazione numerica, e qui ne presentiamo soltanto alcuni,
commentando i rispettivi vantaggi e svantaggi.
Come si è visto nella dimostrazione del teorema della mappa standard , gli scorrimenti sono mappe conservative del piano in se stesso. Perciò, se si vuole in qualche modo approssimare un sistema continuo conservativo con un sistema discreto pure conservativo, si possono cercare dei metodi di approssimazione che consistano in una sequenza di scorrimenti. Questi metodi vanno sotto il nome di metodi simplettici a scorrimento .
Per integrare il sistema dinamico derivato da un sistema newtoniano di dimensione 1

usiamo per esempio una sequenza di tre scorrimenti, alternando l'aggiornamento della x e della y:
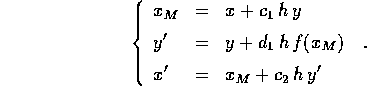
Cerchiamo quindi di determinare i tre coefficienti 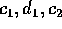 in modo
che il metodo abbia ordine di troncamento 2, cioè con
errore di troncamento locale
in modo
che il metodo abbia ordine di troncamento 2, cioè con
errore di troncamento locale 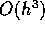 . Per ottenere questo, basta
imporre che risolva esattamente il caso f(x)=2, con soluzione per
esempio
. Per ottenere questo, basta
imporre che risolva esattamente il caso f(x)=2, con soluzione per
esempio 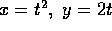 :
:
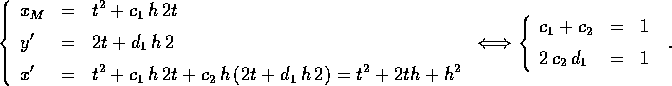
La soluzione non è unica, ma esiste una sola soluzione che ha la
notevole proprietà aggiuntiva di essere reversibile , cioè di
dare (x,y) a partire da (x',y') se il metodo viene applicato con
passo -h; per avere questa proprietà occorre che 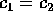 , quindi
la soluzione è
, quindi
la soluzione è 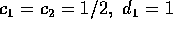 :
:
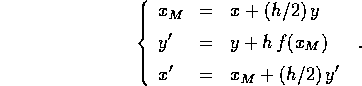
Esempio:
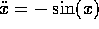 ;
;
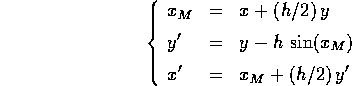
Per confrontare questa approssimazione con quella della mappa standard del pendolo , abbiamo usato nella Figura 4.7 lo stesso valore h=1.
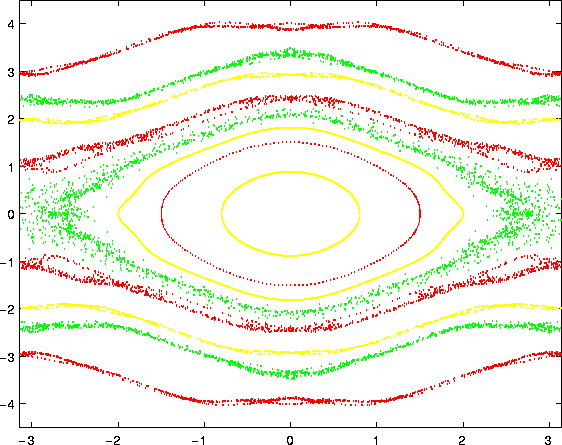
Figure 4.7: Il metodo simplettico a tre scorrimenti e di
ordine due applicato al pendolo nonlineare conservativo, con passo
h=1. Si noti, per confronto con il metodo conservativo di ordine 1
(cioè la mappa standard) usato con lo
stesso passo, che le soluzioni si muovono vicino a curve non troppo
diverse dalle linee di livello dell'integrale dell'energia, con
l'eccezione della regione attorno alla sepratrice.
Per una trattazione più ampia dei metodi di integrazione simplettici si veda [Yoshida 93].
Una classe importante di metodi di integrazione numerica va sotto il nome di Runge e Kutta. Dato il sistema dinamico

un metodo di Runge-Kutta ad s passi intermedi è un sistema
dinamico discreto la cui mappa 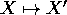 è della forma
è della forma
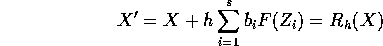
dove h è il passo e
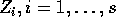 sono
approssimazioni di valori intermedi ottenuti con le formule
sono
approssimazioni di valori intermedi ottenuti con le formule
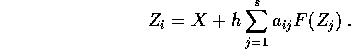
Se la matrice 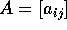 è tale che
è tale che 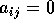 per
per 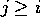 , il
metodo è esplicito ed i valori
intermedi
, il
metodo è esplicito ed i valori
intermedi 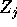 si possono calcolare in sequenza, altrimenti il metodo
è implicito e le equazioni per gli
si possono calcolare in sequenza, altrimenti il metodo
è implicito e le equazioni per gli
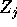 vanno risolte ad ogni passo. La soluzione di questo sistema di
equazioni esiste ed è unica per h abbastanza piccolo; infatti si
tratta di un'equazione del tipo del punto unito , e per h
piccolo il secondo membro è una contrazione (in un intorno di X).
vanno risolte ad ogni passo. La soluzione di questo sistema di
equazioni esiste ed è unica per h abbastanza piccolo; infatti si
tratta di un'equazione del tipo del punto unito , e per h
piccolo il secondo membro è una contrazione (in un intorno di X).
Lo stesso metodo si potrebbe applicare anche ad un sistema di equazioni differenziali non autonomo

con il solito procedimento di omogeneizzazione , cioè
aggiungendo un'equazione per la variabile 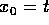 :
:
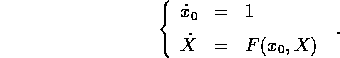
Questo significa usare la formula modificata per il calcolo dei valori intermedi
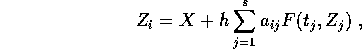
dove i tempi intermedi sono 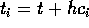 dati dai
coefficienti
dati dai
coefficienti

Lo scopo di un metodo di Runge-Kutta, come di ogni metodo di
integrazione numerica, è quello di approssimare X(t+h) con X',
supponendo che X=X(t). Il principale requisito per un metodo di
integrazione numerica accurato è quello di avere un
ordine di troncamento più grande possibile. L'ordine è q se la
differenza tra l'approssimazione discreta 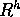 e la soluzione esatta
X(t+h) è infinitesimo di ordine q+1 rispetto al passo h per
e la soluzione esatta
X(t+h) è infinitesimo di ordine q+1 rispetto al passo h per
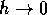 :
:
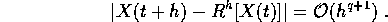
Per imporre che il metodo sia di ordine q si può richiedere che risolva esattamente le equazioni differenziali che hanno come soluzioni dei polinomi di grado fino a q: in altri termini le equazioni

devono essere risolte esattamente. Applicando un metodo di
Runge-Kutta a queste equazioni si trovano delle condizioni
sui coefficienti 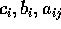 . Se
. Se 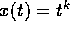 è la
soluzione esatta,
è la
soluzione esatta,
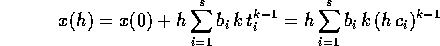
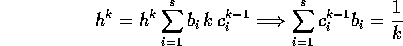
Si noti che se i 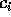 sono già stati scelti, questo è un sistema
lineare con incognite
sono già stati scelti, questo è un sistema
lineare con incognite 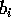 e come matrice dei
coefficienti la matrice di Vandermonde
e come matrice dei
coefficienti la matrice di Vandermonde 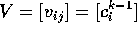 ;
il sistema è quadrato se si richiede che l'ordine sia s, e in tal
caso ha soluzione unica se i
;
il sistema è quadrato se si richiede che l'ordine sia s, e in tal
caso ha soluzione unica se i 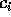 sono diversi tra loro (perché il
determinante della matrice di Vandermonde
sono diversi tra loro (perché il
determinante della matrice di Vandermonde 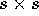 è diverso da zero).
è diverso da zero).
Vediamo allora alcune soluzioni di queste equazioni: per esempio, se cerchiamo un metodo di ordine 2 a 2 passi intermedi, abbiamo un sistema di due equazioni in quattro incognite:
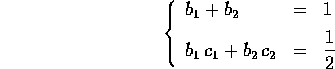
che ha soluzione per ogni coppia di valori diversi di 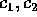 arbitrariamente scelti; per esempio per
arbitrariamente scelti; per esempio per 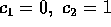 abbiamo
abbiamo
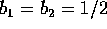 . Bisogna poi soddisfare alle condizioni per cui le
. Bisogna poi soddisfare alle condizioni per cui le 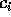 sono somma delle righe di A; l'unica soluzione che dia un metodo
esplicito (con
sono somma delle righe di A; l'unica soluzione che dia un metodo
esplicito (con 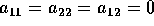 ) è
) è 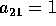 . In
conclusione un metodo di Runge-Kutta esplicito di ordine 2 è dato
dalle formule
. In
conclusione un metodo di Runge-Kutta esplicito di ordine 2 è dato
dalle formule
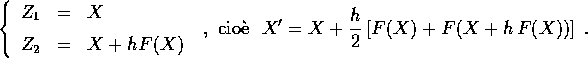
Se invece cerchiamo un metodo ad un solo passo intermedio e di ordine
2, è chiaro che non potrà essere esplicito (avendo una matrice A
di tipo 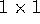 , questa non può essere nulla sulla diagonale,
altrimenti è nulla e si ottiene un metodo di ordine 1). Abbiamo
allora due equazioni, nelle due sole incognite
, questa non può essere nulla sulla diagonale,
altrimenti è nulla e si ottiene un metodo di ordine 1). Abbiamo
allora due equazioni, nelle due sole incognite 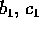 :
:
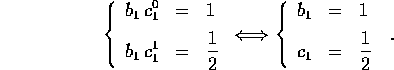
La soluzione in questo caso è unica, con 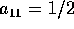 ; il metodo è
implicito, nel senso che il valore intermedio appare nell'equazione
del punto unito:
; il metodo è
implicito, nel senso che il valore intermedio appare nell'equazione
del punto unito:
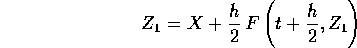
e solo dopo aver risolto questa (per esempio per approssimazioni successive ) si può calcolare il nuovo punto:
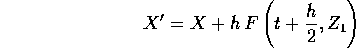
Teorema dei metodi di Runge-Kutta conservativi : Il metodo di Runge-Kutta implicito ad 1 passo intermedio e di ordine 2 è conservativo, nel senso che se applicato ad un sistema newtoniano ad un grado di libertà fornisce un sistema dinamico discreto conservativo.
Dimostrazione omessa.
In effetti vale un risultato molto più generale: se applicato ad un sistema hamiltoniano , il metodo di Runge-Kutta con s=1 ed ordine 2 è un metodo di integrazione simplettico , cioè la mappa del sistema dinamico discreto è una trasformazione canonica . Perciò questo metodo, pur non essendo un'approssimazione accurata del sistema dinamico continuo corrispondente, può essere valida come metodo di integrazione numerica quando abbiano importanza solo le proprietà qualitative della soluzione.
Esempio:
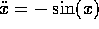 . Ponendo come al solito
. Ponendo come al solito 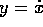 , l'equazione del
punto unito per il valore intermedio
, l'equazione del
punto unito per il valore intermedio 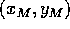 è
è

una volta trovato il punto intermedio (per esempio con il metodo delle approssimazioni successive ), un passo di lunghezza h è approssimato dal sistema dinamico discreto:
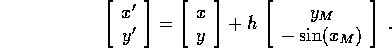
Poiché il sistema dinamico così ottenuto è conservativo, le proprietà di stabilità delle approssimazioni lineari sono conservate; anche alcune proprietà qualitative, come la presenza di curve invarianti, sono conservate, e la regione caotica che circonda la separatrice è di area molto ridotta, persino per valori di h che con altri metodi di discretizzazione danno una larga regione caotica, per esempio h=1 (Figura 4.8).
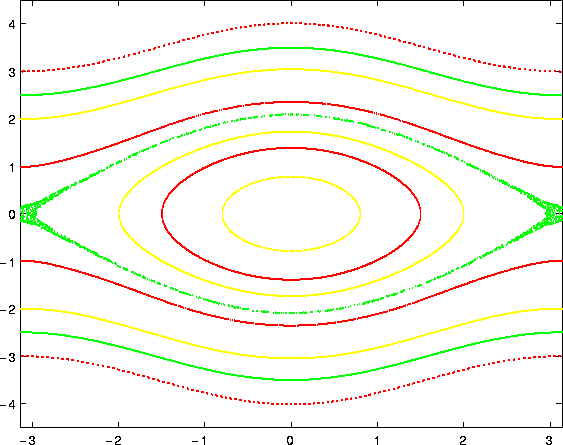
Figure 4.8: L'equazione del pendolo nonlineare conservativo
integrata con il metodo di Runge-Kutta implicito di ordine 2 ad un
solo passo intermedio, e con un passo molto lungo (h=1). Benché il
risultato non sia quantitativamente molto accurato, l'andamento
generale è molto simile a quello del sistema continuo, a parte una
sorprendentemente piccola regione caotica vicino alla separatrice.
La ragione per cui questo metodo è particolarmente efficace nel generare una piccola regione caotica attorno alla separatrice ha a che fare con un'altra proprietà aggiuntiva rispetto a quella di essere simplettico: i metodi di questa classe (di ordine 2s ad s passi intermedi, come il metodo di Runge-Kutta-Gauss ) hanno la proprietà di preservare esattamente le forme quadratiche che siano integrali primi. Quindi nell'intorno del punto di sella nonlineare il comportamento delle soluzioni è descritto in modo molto accurato, perché nell'equazione linearizzata ci sarebbe un integrale primo quadratico.
Costruire metodi con ordine di troncamento superiore al secondo non è tanto facile, ma si conoscono molte soluzioni. Prendiamo per esempio l'ordine 4: il metodo di Runge-Kutta classico (il primo ad essere stato scoperto, ed ancora largamente in uso) è di ordine 4 con 4 passi intermedi, e con la seguente scelta dei tempi intermedi:
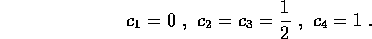
Da qui il sistema di 4 equazioni lineari nelle 4 incognite 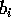
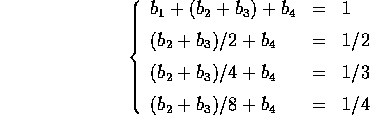
con soluzione unica:
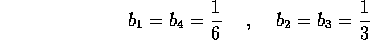
Si definisce così il metodo di Runge-Kutta classico, che può essere espresso in termini dei valori intermedi del secondo membro
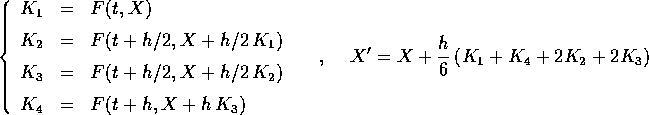
Un metodo di quarto ordine, anche se non ha la proprietà di essere simplettico, può essere usato con un passo abbastanza piccolo per ottenere soluzioni che siano quantitativamente molto simili a quelle esatte (Figura 4.9). Bisogna però fare attenzione a non usare il risultato dell'integrazione numerica per dedurne delle proprietà qualitative; per esempio, in un sistema newtoniano si introduce una ``dissipazione numerica''.
A titolo di esempio di un metodo ancora più accurato, che però richiede un numero maggiore di valutazioni del secondo membro per ogni passo, diamo i coefficienti dell'unico metodo implicito di ordine 4 a due passi intermedi, detto metodo di Runge-Kutta-Gauss :
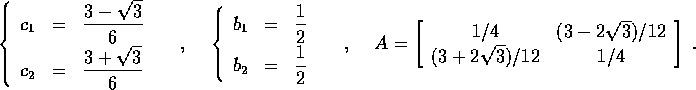
Anche il metodo di Gauss è un metodo di integrazione simplettico , ed ha proprietà di stabilità molto forti: per esempio, è stabile se applicato a qualsiasi sistema lineare stabile.
Per una trattazione completa delle proprietà note dei metodi di integrazione numerica di Runge-Kutta si veda [Butcher 87].
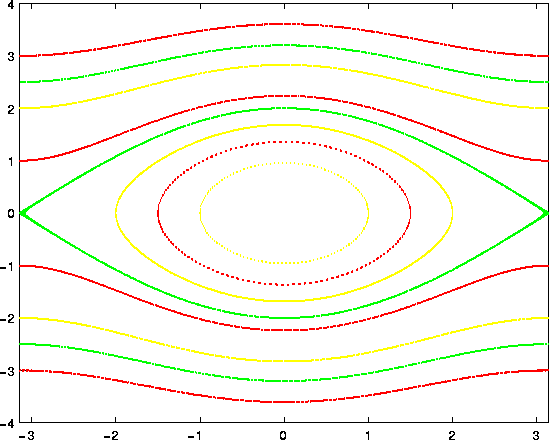
Figure 4.9: Il pendolo nonlineare conservativo integrato con il
metodo di Runge-Kutta classico, di ordine 4 e a 4 passi intermedi,
con un passo abbastanza corto (h=0.2). Il risultato appare molto
simile alla soluzione esatta, ma se l'integrazione continuasse per un
tempo molto lungo l'effetto dissipativo introdotto dalla
discretizzazione diventerebbe evidente, per esempio osservando
l'andamento nel tempo dell'integrale primo dell'energia.
\