Sommario Molti esempi di hamiltoniane che non sono del tipo semplice
H(p,q)=T(p)+V(q) si ottengono per trasformata di Legendre a partire
dalle equazioni di Lagrange. I casi più notevoli sono quelli dei
moti vincolati, sia di corpi puntiformi, sia di corpi dotati di momento
d'inerzia non nullo (purché lo spazio delle configurazioni resti ad
una dimensione). Molti esempi si possono ricavare anche da problemi non
strettamente meccanici. La condizione che la funzione energia
potenziale sia di classe 
può essere rilassata.
Molti sistemi hamiltoniani non sono della forma che deriva da un
sistema newtoniano ad un grado di libertà. Alcuni sistemi
hamiltoniani ad un grado di libertà possono essere ricavati da
sistemi newtoniani con più gradi di libertà in presenza di
vincoli. Il caso più importante è quello del
moto vincolato di un corpo puntiforme ;
con questo si intende che un corpo puntiforme
di massa m si muova nello spazio 
su di una curva X=X(q) con
parametro q; la curva si suppone che sia regolare, di classe
per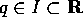 
. Allora l'energia cinetica del corpo
puntiforme sarà semplicemente
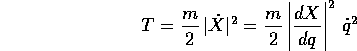
una funzione quadratica di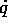 
, che soddisfa la condizione di
convessità perché il coefficiente di 
è maggiore di
0, e che dipende anche da q: quindi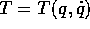 
.
Non è facile dare una definizione fisica di corpo puntiforme , visto che si tratta in realtà di un'astrazione matematica. La definizione più chiara è questa: si tratta di un corpo per il quale l'energia cinetica è fornita solo dal movimento di un singolo punto rappresentativo (in pratica il suo centro di massa), ed è trascurabile qualsiasi contributo proveniente per esempio dall'energia cinetica dei moti di rotazione; quindi l'energia cinetica è data, per definizione, dalla formula precedente.
Supponiamo che le forze esterne siano dotate di energia potenziale W(X); allora la funzione composta, in sostanza la restrizione dell'energia potenziale alla curva, V(q)=W(X(q)), avrà come derivata rispetto a q
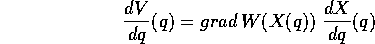
che è (a meno del segno) la componente lungo la tangente alla curva
della forza applicata al corpo puntiforme dal campo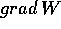 
. Se
facciamo l'ipotesi che le componenti delle forze normali alla curva
siano annullate dalle reazioni vincolari , che appunto forzano
il moto a restare confinato alla curva, ma hanno componente nulla
lungo la tangente alla curva, allora l'equazione di moto lungo la
curva sarà esprimibile mediante la lagrangiana
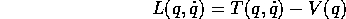
ossia dall'equazione di Lagrange :
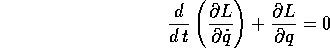
e sostituendo le equazioni per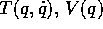 
, il momento è
e l'equazione di Lagrange è
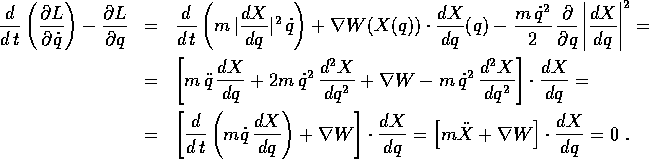
Quindi l'equazione di Lagrange esprime il fatto che l'accelerazione
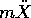subita dal corpo puntiforme è compensata dalla forza
esterna di potenziale W soltanto per la componente nella direzione
tangente alla curva di vincolo; la componente normale alla curva
contiene anche le reazioni vincolari, la cui intensità è
arbitraria. Perciò l'equazione di Lagrange è equivalente alle
equazioni di Newton nell'ipotesi che il vincolo sia rispettato.
Esempio:
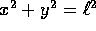, sotto l'azione di un
campo di forze con energia potenziale W(x,y)=mgy (per esempio per
effetto di un campo di gravità costante rivolto in direzione
dell'asse y negativo, e di intensità costante g; ma si badi
che ai fini delle equazioni di moto non ha importanza quale è la
causa fisica della forza). Il corrispondente sistema dinamico - sia
esso espresso con l'equazione di Lagrange oppure con le equazioni di
Hamilton - è il pendolo (nonlineare conservativo).
Se parametrizziamo la circonferenza del vincolo con l'angolo 
misurato a partire dal ``basso'' (cioè dall'asse y negativo), allora
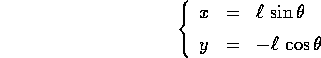
e per calcolare la funzione di Lagrange
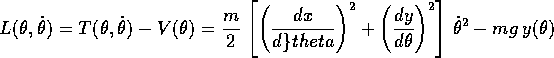
basta calcolare le derivate della curva rispetto alla parametrizzazione:
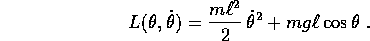
La costante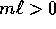 
moltiplica la lagrangiana che si potrebbe
dividere per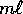 
senza inconvenienti.
Il momento è quindi
e l'equazione di Lagrange è
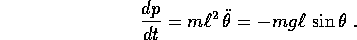
La trasformata di Legendre definisce una funzione hamiltoniana
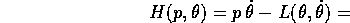
che risulta, sostituendo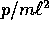 
al posto di 
:
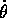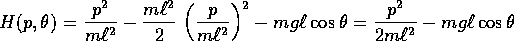
Il sistema può anche essere ridotto alla forma newtoniana
dividendo la lagrangiana per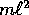 
(e quindi ponendo 
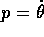, il momento uguale alla
velocità angolare ),
e in questa forma è già stato
studiato nella Sezione 3.4.
Il fatto che lo spazio delle configurazioni ,
cioè l'insieme in cui può muoversi il vettore di stato (x,y),
sia una circonferenza rende possibile spiegare in modo razionale la
natura della
coordinata lagrangiana
. In effetti il
punto materiale appartiene ad una circonferenza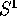 
, che è una
curva regolare, cioè una varietà differenziabile di dimensione 1:
è una variabile reale che viene
impiegata come carta coordinata di 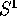. Allora
la definizione di una variabile angolo è quella
della carta coordinata, cioè un'applicazione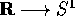 
;
con il simbolo si indicano ambiguamente sia la
variabile indipendente che la carta, e quindi si può
considerare sia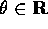 
che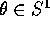 
, ma di
volta in volta bisogna specificare chiaramente cosa si intende.
Esercizio
Fissando una delle estremità di un filo inestendibile di lunghezza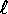 
ad un punto materiale di massa m, e l'altra estremità al punto
più alto di una guida circolare di raggio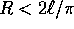 
(cfr. figura 5.5).
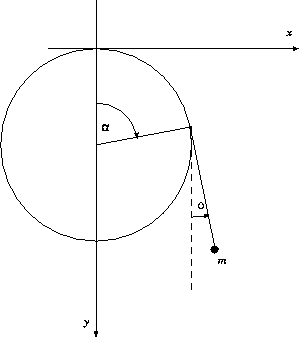
Figure 5.5: Pendolo di lunghezza variabile
Studiare il moto del pendolo sul piano verticale della guida e determinare la frequenza delle piccole oscillazioni intorno al punto di equilibrio stabile.
Suggerimento: Come coordinata, servirsi di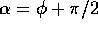 
, dove 
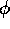è
l'angolo formato dalla direzione del filo con la verticale.
Esempio:
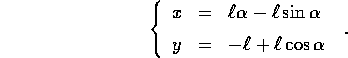
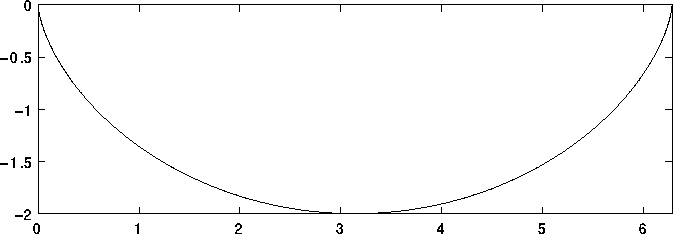
Figure 5.6: Pendolo cicloidale: la cicloide
è ottenuta facendo rotolare senza strisciare una ruota (su di
una rotaia posta in alto); per ogni giro della ruota c'è una
posizione di equilibrio stabile, e le oscillazioni attorno
a questo minimo sono isocrone, non solo per piccole ampiezze, ma per
ogni ampiezza di oscillazione fino a raggiungere i punti di cuspide,
in cui la curva non è regolare.
Supponiamo per semplicità di calcolo che il raggio della ruota sia
.
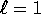Si noti che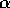 
non è una variabile angolo, perché la
parametrizzazione della curva non è periodica. Il moto è quello
di un punto su di una ruota che, senza strisciare, rotola
lungo il soffitto.
Le equazioni di Lagrange nella variabile 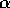sono complicate,
ma è possibile semplificarle usando il parametro arco
s, il quale è definito dalla condizione che il vettore
velocità della curva rispetto ad s sia di lunghezza 1; come è
noto il parametro arco ha la proprietà di misurare la
lunghezza della curva , cioè l'incremento di s su di un
tratto di curva è la sua lunghezza. Per determinare s si usa la
condizione
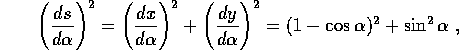
da cui l'equazione a variabili separabili che lega s ad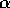
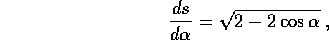
che si risolve con la quadratura
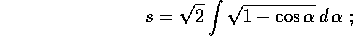
per sostituzione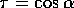 
, con
,
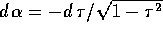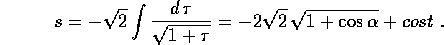
Ne segue una notevole semplificazione della parametrizzazione per la
coordinata y; prendendo la costante arbitraria nella definizione
di s uguale a zero (l'origine del parametro arco sta nel punto
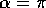, cioè nel punto più in ``basso''), si ottiene
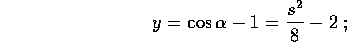
se poi supponiamo che il corpo vincolato sia sottoposto ad
un'accelerazione di gravità di intensità g rivolta verso le
y negative, cioè ancora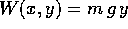 
, ne risulta la
lagrangiana nella coordinata s:
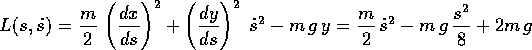
e l'equazione di Lagrange è quella di un oscillatore armonico:
Ne segue che il pendolo cicloidale è perfettamente isocrono,
non solo per le piccole oscillazioni. Si badi però che la
parametrizzazione cessa di essere regolare per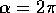 
ed
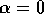, ossia per 
.
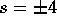La possibilità di scrivere l'equazione di Lagrange nella
coordinata s anziché nella coordinata 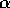segue dal teorema
di covarianza dell'equazione di Lagrange .
Esempio:
, allora l'energia
cinetica si calcola usando la parametrizzazione (x,f(x)):
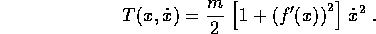
Se facciamo la solita assunzione del campo di forze di intensità mg rivolte verso le y negative, si ottiene
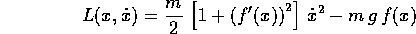
La corrispondente hamiltoniana si calcola a partire dalla trasformata di Legendre inversa:
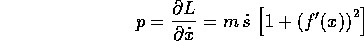
e risulta
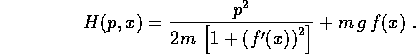
Se invece si usa come parametro sulla curva y=f(x) il parametro
arco s, allora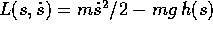 
dove y=h(s) è
la parametrizzazione della y mediante s. Però non è detto
che sia semplice calcolare l'integrale che definisce s e poi
invertire la relazione tra x ed s, salvo che per funzioni f(x)
molto particolari.
Esercizio Studiare il moto di corpi puntiformi, su cui agisce una forza verso le y negative e di intensità costante g, vincolati ai seguenti grafici:
Il primo esercizio corrisponde all'esempio di hamiltoniana che non proviene da un sistema newtoniano, proposto nella Sezione 5.1. (Soluzione)
Esercizio Un corpo puntiforme di massa m viene lanciato verso l'alto, in direzione perfettamente verticale, sotto l'attrazione della gravità terrestre con energia potenziale (in funzione della coordinata verticale z):
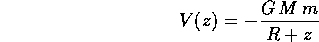
dove G,M,R sono costanti positive (G è la costante di gravitazione universale; M la massa della Terra; R il raggio del nostro pianeta, supposto a perfetta simmetria sferica). Il moto può svolgersi soltanto in direzione radiale (per ragioni di simmetria, non è necessario un vincolo). Trovare la funzione di Hamilton e determinare le condizioni iniziali che danno luogo ad un moto illimitato. Per le soluzioni limitate determinare il tempo impiegato a partire dalla superficie (z=0) per ritornare alla superficie. (Soluzione)
Esercizio Consideriamo un corpo puntiforme di massa m vincolato all'elica cilindrica
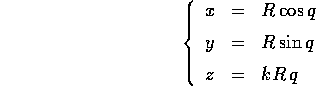
con 
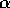, è la pendenza. Se l'energia
potenziale è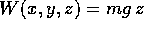 
, scrivere le funzioni di Lagrange e
di Hamilton, e le soluzioni.
(Soluzione)
Se un corpo non è puntiforme, per definizione la sua energia
cinetica non si riduce alla sola energia cinetica di
traslazione. Supponiamo che il corpo sia libero di ruotare soltanto
attorno ad un asse con direzione fissa, e sia l'angolo di
rotazione: allora l'energia cinetica di rotazione sarà della forma
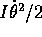, dove il coefficiente I è il
momento d'inerzia rispetto all'unico asse di rotazione.
Per esempio, per un cilindro di raggio R e massa m che ruota
attorno all'asse di simmetria, se la densità è uniforme il momento
d'inerzia è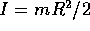 
. Per una sfera di densità uniforme
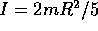. In generale il momento d'inerzia sarà sempre della
forma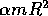 
se m è la massa del corpo ed R una
lunghezza caratteristica della sua forma, dove il coefficiente
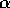dipende sia dalla forma che dalla distribuzione interna di
massa. Per una discussione del momento d'inerzia e del modo di
calcolarlo si veda nella Sezione 7.3.
Esempio:
l'angolo di rotazione
della pallina (attorno ad un asse orizzontale), con l'origine degli
angoli scelta in modo tale da corrispondere all'origine della
coordinata q lungo il pendio: il vincolo è dato dalla condizione
di non strisciare, cioè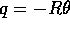 
(dove R è il raggio della
sfera, il segno meno perché la rotazione è in verso orario se la
coordinata q cresce sulla destra).
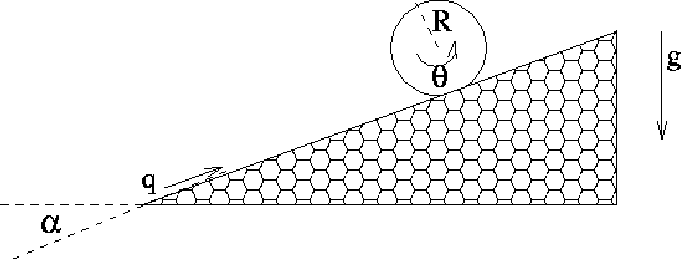
Figure 5.7: L'esperimento di Galileo
con una pallina che rotola su di un piano inclinato.
Allora l'energia cinetica, somma di quella di traslazione di un corpo puntiforme con la stessa massa della pallina e di quella di rotazione, è:
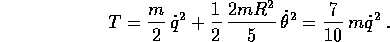
Se l'angolo formato dal piano inclinato con l'orizzontale è
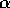(con il piano in salita al crescere di q),
e l'accelerazione di gravità ha intensità g, l'energia
potenziale è
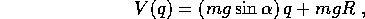
quindi la lagrangiana è, a meno di una costante additiva:
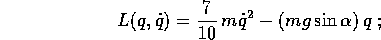
si noti che non dipende da R, per ogni R>0. Se si considera che la lagrangiana di un corpo in caduta verticale libera lungo l'asse z con gravità w è:
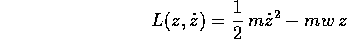
le due lagrangiane esprimono dinamiche equivalenti (perché sono proporzionali, con costante di proporzionalità 7/5) se
L'esperimento di Galileo è quindi un esperimento sui moti
uniformemente accelerati, ma graduando l'angolo di pendenza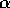
si possono ottenere accelerazioni molto minori di g; questo era lo
scopo di Galileo nell'usare il piano inclinato, vista la
difficoltà di misurare accuratamente i tempi. Si noti che il
limite per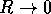 
non è possibile, perché la velocità alla
periferia del corpo rotante tenderebbe all'infinito; in effetti
l'approssimazione del corpo puntiforme conduce ad un risultato
diverso.
Se si sostituisce la sfera con un cilindro di momento di inerzia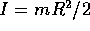
la relazione con la caduta libera diventa
Il formalismo lagrangiano, e quello hamiltoniano, hanno applicazioni anche al di fuori della meccanica classica; di questo diamo due esempi semplici.
Esempio:
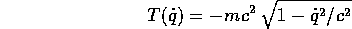
dove la costante c>0 rappresenta la velocità della luce, e
la velocità della particella è limitata da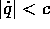 
.
Il segno meno garantisce che l'energia cinetica sia è convessa,
quindi la relazione tra 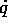e p sia monotona crescente.
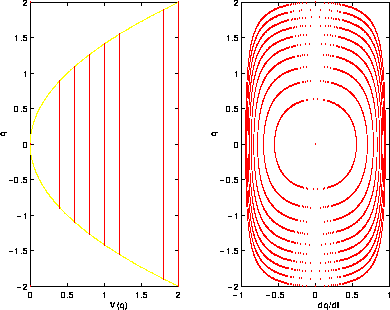
Figure 5.8: Formulazione hamiltoniana della meccanica
relativistica ad un grado di libertà: a sinistra le curve sono sovrapposte al grafico (V(q),q), a destra H(p,q)=E per gli
stessi valori di E. Si noti che per grandi ampiezze di oscillazione
la velocità diventa minore di quella dell'oscillatore classico,
dovendo rimanere minore di quella della luce c. Queste figure sono
state tracciate assumendo c=1.
La trasformata di Legendre è
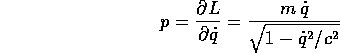
quindi la hamiltoniana, che esprime la conservazione dell'energia, si ottiene da
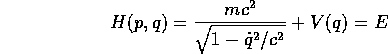
sostituendo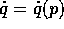 
.
Consideriamo per esempio il moto sotto l'azione di una forza con energia potenziale quadratica
con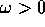 
(che è la frequenza nel caso classico).
Fissato E, le linee di livello si possono
descrivere esplicitando :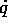
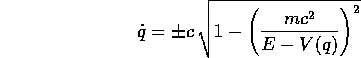
per i valori di q tali che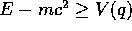 
.
Questo esempio è più semplice dei casi fisicamente significativi. Per una trattazione della meccanica coerente con la relatività ristretta, consultare [Goldstein 1950], Capitolo 6; per la formulazione lagrangiana, vedere in particolare pag. 205-207.
Esercizio
Una particella di massa m e carica positiva Q è vincolata a
muoversi lungo un'asta lunga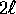 
, ai cui estremi sono fissate due
cariche uguali di valore -Q e massa trascurabile. Studiare
l'hamiltoniana del sistema nel piano delle fasi. Determinare il
periodo delle oscillazioni ottenute liberando la particella, con
velocità iniziale nulla, in un punto distante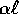 
( 
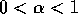) dal punto medio dell'asta.
(Soluzione)
La condizione che la funzione di Hamilton, e quella di Lagrange, siano
di classe , è conveniente nelle dimostrazioni ma non è
indispensabile. Il teorema di
esistenza e unicità
richiede che il secondo membro di un
sistema dinamico sia una funzione lipschitziana , quindi
continua ma non necessariamente differenziabile. Per esempio, in un
sistema hamiltoniano (proveniente da uno newtoniano)
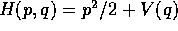, supponiamo che f(q)=-V'(q) sia 
ovunque
salvo che in un numero finito di punti, nei quali ammette derivata destra e
sinistra. La funzione f(q) risulta comunque localmente
lipschitziana, e l'esistenza e unicità della soluzione sono
assicurate anche quando essa passa da questi punti singolari.
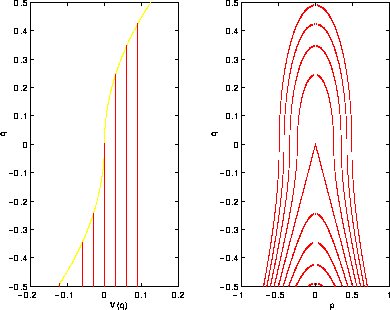
Figure 5.9: Il piano delle fasi delle variabili
(p,q) per un sistema newtoniano con forza pari a meno il
modulo della coordinata q. Tutte le soluzioni sono
definite per ogni t, e tutte tranne tre orbite hanno
insiemi limite vuoti (cioè vanno all'infinito).
Esempio:
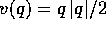, che è e con derivata
V'(q)=|q|, che è lipschitziana (con costante di Lipschitz 1).
Ne segue che sia il sistema hamiltoniano
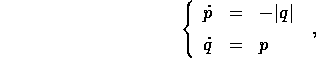
sia il sistema lagrangiano
hanno soluzioni ben definite ed uniche per ogni condizione iniziale, comprese quelle con q(0)=0. Lo studio delle linee di livello
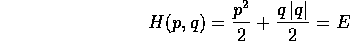
mostra che c'è un insieme di livello per E=0 che non è una
curva regolare, ed è una separatrice che consiste di tre
traiettorie, cioè il punto di equilibrio, una con l'equilibrio
come limite ed una con l'equilibrio come 
limite.
Tutte le altre orbite hanno per immagine curve aperte.
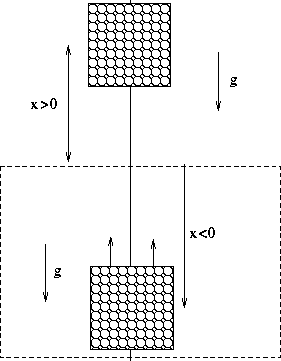
Figure 5.10: Il galleggiante libero di muoversi
solo verticalmente riceve una spinta che non è derivabile al
momento dell'emersione (sia della faccia superiore che di
quella inferiore del galleggiante). Nel piano delle fasi ne
risultano curve di livello della hamiltoniana che si
raccordano in modo differenziabile ma non differenziabile due volte.
Si può applicare il formalismo lagrangiano e/o hamiltoniano a
corpi galleggianti, usando nel calcolo delle forze - e quindi
dell'energia potenziale - la legge di Archimede : un corpo
immerso in un liquido riceve dal liquido stesso una spinta pari al
peso del liquido spostato; il potenziale risulta solo , e non
al momento dell'emersione, ma l'accelerazione è
lipschitziana e quindi l'esistenza e unicità della soluzione è
garantita.
Esercizio
Lungo un'asta verticale scorre senza dissipazione un cubo omogeneo di
lato 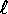e densità d; l'asta è parzialmente immersa in un
liquido di densità a, con a>d; il cubo è soggetto alla forza
di gravità con accelerazione g verso il basso, e alla forza di
Archimede.
Si descriva il moto con formalismo hamiltoniano, nelle variabili x (dove x è l'altezza del centro del cubo rispetto al pelo del liquido) e
Da quale profondità deve essere rilasciato il cubo con velocità
iniziale zero per uscire dal liquido fino all'altezza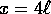 
?
Suggerimento: Se il peso del cubo è P, la forza di Archimede è:
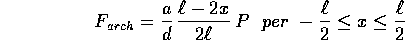
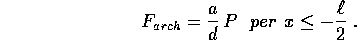
Si può rispondere alla seconda domanda indipendentemente dalla prima, usando soltanto l'integrale dell'energia.
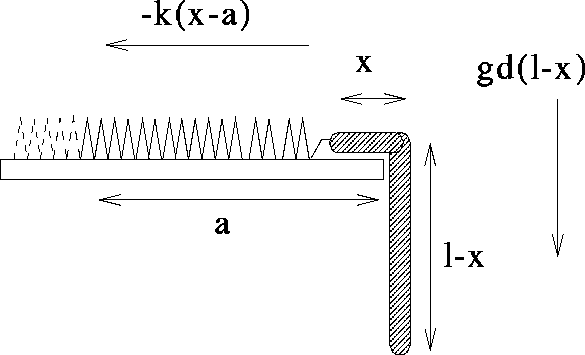
Figure 5.11: Il filo che può scivolare oltre l'orlo di un
piano orizzontale riceve una spinta che non è derivabile al momento
in cui ciascuna delle due estremità del filo passa dall'orlo. Nel
piano delle fasi ne risultano curve di livello della hamiltoniana che
si raccordano, lungo due rette, in modo differenziabile ma non
differenziabile due volte.
Un altra classe di problemi sui sistemi conservativi si ottiene
considerando il filo inestendibile pesante , con densità
lineare costante; non serve solo ad imporre un vincolo, ma
contribuisce sia all'energia cinetica che a quella potenziale. Si
intende che il filo possa piegarsi senza sforzo, e scivolare su di una
superficie (con o senza dissipazione); però in presenza di uno
spigolo, il potenziale risulta e non , pur mantenendo
l'unicità delle soluzioni per la condizione di Lipschitz.
Esercizio
Sia dato un filo inestendibile pesante, di densità lineare costante
d e lunghezza 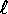, attaccato ad una molla di costante elastica
k. Supponiamo che la molla sia sufficientemente lunga e che la sua
posizione di equilibrio
disti a dal ciglio dello strapiombo (Figura 5.11),
al di là del quale il filo pesante si piega e scende attratto dalla
gravità g. Sul piano di appoggio il filo scivola senza dissipazione.
Si descriva il moto (nel piano delle fasi) utilizzando le ipotesi: (1)
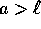; (2) dg>k; (3) 
.
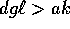Descrivere che cosa cambia s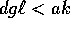e 
.
(Soluzione)