



Next: 6.4 SIMMETRIEINTEGRALI PRIMI
Up: 6 SISTEMI CONSERVATIVI: PIÙ
Previous: 6.2 TRASFORMATA DI LEGENDRE
Sommario Molti sistemi meccanici hanno degli spazi delle
configurazioni che non sono aperti di 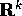 , ma che possono
essere descritti da carte locali con coordinate in
, ma che possono
essere descritti da carte locali con coordinate in 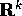 .
Questo si verifica per i moti vincolati di sistemi
composti da più corpi puntiformi, o anche da sistemi estesi
rigidi o parzialmente rigidi. Le equazioni di Lagrange
e di Hamilton possono essere ugualmente impiegate per
descrivere la dinamica, in ciascuna carta locale; le
proprietà globali delle soluzioni possono però richiedere
uno studio attento delle proprietà globali dello spazio
delle configurazioni.
.
Questo si verifica per i moti vincolati di sistemi
composti da più corpi puntiformi, o anche da sistemi estesi
rigidi o parzialmente rigidi. Le equazioni di Lagrange
e di Hamilton possono essere ugualmente impiegate per
descrivere la dinamica, in ciascuna carta locale; le
proprietà globali delle soluzioni possono però richiedere
uno studio attento delle proprietà globali dello spazio
delle configurazioni.
Lo spazio delle configurazioni a cui appartiene il vettore di
stato X di un sistema
meccanico può essere definito come sottoinsieme di uno
spazio 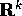 per mezzo di condizioni o vincoli ,
espressi da equazioni di
varia natura. I vincoli espressi in modo indipendente dal
tempo con equazioni del
tipo f(X)=0, con f una funzione differenziabile, si
chiamano vincoli olonomi .
per mezzo di condizioni o vincoli ,
espressi da equazioni di
varia natura. I vincoli espressi in modo indipendente dal
tempo con equazioni del
tipo f(X)=0, con f una funzione differenziabile, si
chiamano vincoli olonomi .
Il caso più semplice è quello in cui il sistema consiste
di n corpi puntiformi ,
ciascuno con posizione 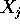 e massa
e massa
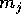 . Allora
. Allora 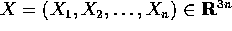 è il
vettore di stato, che esprime la posizione di tutti i corpi.
Gli n corpi avranno un moto vincolato se la loro
posizione è sottoposta
a condizioni della forma
è il
vettore di stato, che esprime la posizione di tutti i corpi.
Gli n corpi avranno un moto vincolato se la loro
posizione è sottoposta
a condizioni della forma
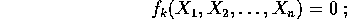
l'esempio più ovvio è quello in cui le distanze tra alcuni
dei punti sono fisse, oppure alcuni dei punti sono fissi.
Esempio:
Esempio:
Se i due punti sono di massa uguale, e si considera che
non ci sia modo di distinguerli, allora lo spazio delle
configurazioni è il quoziente di 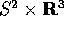 per le
identificazioni dei punti antipodali sulla sfera, quindi è
il prodotto del piano proiettivo per
per le
identificazioni dei punti antipodali sulla sfera, quindi è
il prodotto del piano proiettivo per 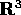 , e non può
essere una sottovarietà di
, e non può
essere una sottovarietà di 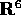 (ma può essere immerso
in
(ma può essere immerso
in 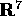 ). Capita spesso che i sistemi con identificazioni, in
cui si passa al quoziente rispetto a qualche simmetria, siano
geometricamente più complessi.
). Capita spesso che i sistemi con identificazioni, in
cui si passa al quoziente rispetto a qualche simmetria, siano
geometricamente più complessi.
Esempio:
-
- Un sistema formato da tre corpi puntiformi, con distanze fisse
tra loro:
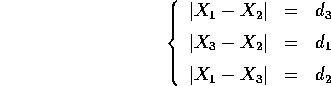
è l'esempio più semplice di corpo rigido , in cui
tutte le distanze sono fisse. Se supponiamo che i tre corpi
non siano allineati, lo spazio delle configurazioni
è un sottoinsieme di 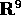 , ma, poiché ci sono 3 vincoli,
il numero di gradi di libertà è 6.
, ma, poiché ci sono 3 vincoli,
il numero di gradi di libertà è 6.
Esempio:
In tutti questi casi, e anche in molti altri, lo spazio delle
configurazioni può essere descritto da vincoli olonomi, ossia come
l'insieme degli
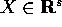 tale che
tale che

dove 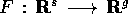 è
un'applicazione di classe
è
un'applicazione di classe  .
Per il teorema delle funzioni implicite , se la
matrice jacobiana
.
Per il teorema delle funzioni implicite , se la
matrice jacobiana 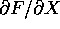 ha rango g in un
punto
ha rango g in un
punto 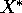 , allora esiste un'applicazione di classe
, allora esiste un'applicazione di classe 

definita in un intorno opportuno W di 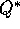 in
in 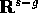 tale che
tale che
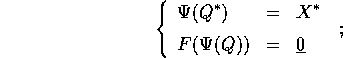
l'insieme (s-g)-dimensionale dei punti che
rispettano il vincolo è così parametrizzato in modo surgettivo.
In altre parole, il teorema delle funzioni implicite assicura
che se i vincoli sono funzionalmente indipendenti ,
cioè con gradienti linearmente indipendenti, in un punto
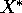 , allora esiste una carta locale dello spazio delle
configurazioni -che copre tutti e soli i punti che rispettano il vincolo,
in un intorno di
, allora esiste una carta locale dello spazio delle
configurazioni -che copre tutti e soli i punti che rispettano il vincolo,
in un intorno di 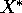 - con un numero di coordinate Q pari alla
differenza fra la
dimensione dello spazio ambiente ed il numero di vincoli.
Le variabili Q si chiamano coordinate lagrangiane .
- con un numero di coordinate Q pari alla
differenza fra la
dimensione dello spazio ambiente ed il numero di vincoli.
Le variabili Q si chiamano coordinate lagrangiane .
Le coordinate lagrangiane sono definite da una carta locale, ma
per coprire l'intero spazio delle configurazioni, che in è dotato di
una struttura di varietà differenziabile , occorrono di solito più carte locali: tra due
sistemi di coordinate lagrangiane esistono dei cambiamenti di
coordinate che sono diffeomorfismi, della stessa classe di
differenziabilità delle equazioni di vincolo, nelle nostre ipotesi
di classe  .
.
Supponiamo ora che la forza agente sul sistema possa essere decomposta
nella somma di una forza derivante da un campo conservativo con
energia potenziale 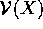 e di una forza derivante dalle
reazioni vincolari , che costringono il moto a rispettare i
vincoli. Supponiamo inoltre che vi siano dei vincoli lisci ,
cioè le componenti delle reazioni vincolari in direzioni tangenti al
vincolo siano nulle. Allora, se
e di una forza derivante dalle
reazioni vincolari , che costringono il moto a rispettare i
vincoli. Supponiamo inoltre che vi siano dei vincoli lisci ,
cioè le componenti delle reazioni vincolari in direzioni tangenti al
vincolo siano nulle. Allora, se 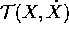 è l'energia
cinetica, il moto del sistema potrà essere studiato, nel senso che
sarà precisato di seguito, per mezzo della funzione di Lagrange
è l'energia
cinetica, il moto del sistema potrà essere studiato, nel senso che
sarà precisato di seguito, per mezzo della funzione di Lagrange
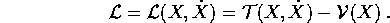
Se una curva X(t) rispetta il vincolo 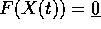 ,
allora la sua velocità soddisfa le condizioni che si ottengono
derivando rispetto al tempo questa equazione, cioè
,
allora la sua velocità soddisfa le condizioni che si ottengono
derivando rispetto al tempo questa equazione, cioè
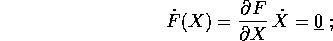
perciò in ogni punto dello spazio delle configurazioni la
velocità è perpendicolare ai gradienti 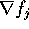 delle
funzioni vincolari
delle
funzioni vincolari 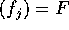 . Lo spazio vettoriale dei
vettori che rispettano questa condizione ha dimensione s-g=b
e si chiama spazio tangente alla varietà dei vincoli nel
punto dato.
. Lo spazio vettoriale dei
vettori che rispettano questa condizione ha dimensione s-g=b
e si chiama spazio tangente alla varietà dei vincoli nel
punto dato.
Derivando ancora una volta rispetto al tempo, si possono determinare
quali reazioni vincolari sono necessarie per mantenere una soluzione
X(t) soddisfacente ai vincoli:
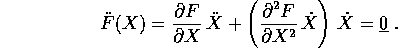
Questa relazione, per la condizione di perpendicolarità appena
vista, coinvolge solamente le componenti dell'accelerazione 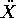 che si trovano nello spazio normale (dei vettori perpendicolari allo
spazio tangente). Ne segue che reazioni vincolari perpendicolari allo
spazio tangente sono sufficienti a garantire il rispetto del vincolo,
e le equazioni di moto saranno della forma
che si trovano nello spazio normale (dei vettori perpendicolari allo
spazio tangente). Ne segue che reazioni vincolari perpendicolari allo
spazio tangente sono sufficienti a garantire il rispetto del vincolo,
e le equazioni di moto saranno della forma
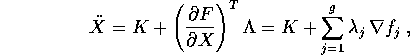
dove K è la parte dell'accelerazione dovuta alla
forza esterna (perciò derivata dall'energia potenziale
V(X)), mentre la parte perpendicolare allo spazio tangente
contiene i moltiplicatori di Lagrange arbitrari
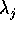 .
.
Esempio:
-
- Supponiamo s=3, g=1, cioè prendiamo il caso di una
superficie definita da un solo vincolo f(X)=0 nello spazio
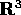 . Se
. Se 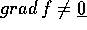 , esiste una carta locale
con due coordinate lagrangiane
, esiste una carta locale
con due coordinate lagrangiane 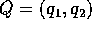 . Se X(t) è
una curva che appartiene alla superficie (identicamente
rispetto a t), allora la sua velocità
. Se X(t) è
una curva che appartiene alla superficie (identicamente
rispetto a t), allora la sua velocità
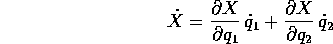
appartiene al piano tangente generato dai due vettori tangenti
alle linee coordinate 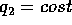 e
e 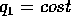 , ed è
ortogonale al gradiente del vincolo:
, ed è
ortogonale al gradiente del vincolo:
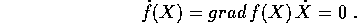
Derivando ancora una volta rispetto al tempo si
ottiene una condizione sull'accelerazione:
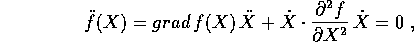
per la quale la componente dell'accelerazione perpendicolare al
piano tangente dipende da una forma quadratica nella
velocità: se si normalizza il vincolo in modo che (nel punto
dato) 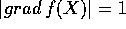 , la forma quadratica in questione è
la seconda forma fondamentale della superficie.
, la forma quadratica in questione è
la seconda forma fondamentale della superficie.
L'ipotesi che i moltiplicatori di Lagrange possano assumere
valori arbitrariamente grandi - quindi che le reazioni vincolari
possano essere di intensità arbitrariamente grande - corrisponde
all'idea di un vincolo di rigidità infinita e capace di resistere ad
ogni sforzo. È evidentemente un'astrazione che poco ha a che fare
con il comportamento reale di rotaie ... e simili. Come si vede
dall'equazione per 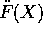 , per velocità
, per velocità 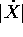 troppo
grandi le reazioni vincolari saranno troppo grandi rispetto alle
proprietà di materiali reali, e il modello dei moti vincolati non
sarà applicabile.
troppo
grandi le reazioni vincolari saranno troppo grandi rispetto alle
proprietà di materiali reali, e il modello dei moti vincolati non
sarà applicabile.
Vogliamo trovare le equazioni di moto di un sistema vincolato, con
vincoli olonomi e
lisci . A questo scopo possiamo utilizzare
la carta locale X=X(Q), la cui esistenza è garantita dal teorema
delle funzioni implicite. È utile ricordare un' altro aspetto di
questo teorema: poiché la carta locale parametrizza lo spazio delle
configurazioni, se 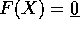 sono i vincoli, allora
sono i vincoli, allora
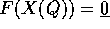 , e derivando rispetto alle coordinate
lagrangiane Q
, e derivando rispetto alle coordinate
lagrangiane Q
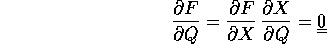
si ottiene la matrice zero. Considerando il prodotto di due
matrici riga per colonna contenuto nella formula precedente,
ogni coefficiente zero nella matrice nulla indica una
relazione di ortogonalità tra il gradiente di una delle
equazioni di vincolo e la velocità rispetto ad una delle
coordinate lagrangiane:

Il teorema delle funzioni implicite assicura anche che la
matrice jacobiana della carta locale 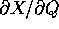 ha rango massimo b, quindi i vettori
ha rango massimo b, quindi i vettori 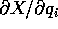 sono una base dello spazio tangente. Questo è il punto
critico nella dimostrazione che è possibile utilizzare il
formalismo lagrangiano per i moti vincolati (se i vincoli sono lisci).
sono una base dello spazio tangente. Questo è il punto
critico nella dimostrazione che è possibile utilizzare il
formalismo lagrangiano per i moti vincolati (se i vincoli sono lisci).
Teorema dei moti vincolati :
Siano 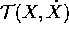 l'energia cinetica e
l'energia cinetica e 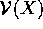 l'energia
potenziale (entrambe di classe
l'energia
potenziale (entrambe di classe  ) di un sistema descritto dal
vettore di stato
) di un sistema descritto dal
vettore di stato 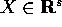 e soggetto alla condizione
e soggetto alla condizione
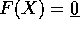 , dove
, dove 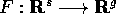 (di classe
(di classe
 ) esprime g vincoli funzionalmente indipendenti in ogni
punto dello spazio delle configurazioni.
) esprime g vincoli funzionalmente indipendenti in ogni
punto dello spazio delle configurazioni.
Se 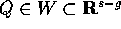 sono le coordinate lagrangiane di una carta locale, allora le
equazioni di Lagrange sull'insieme W:
sono le coordinate lagrangiane di una carta locale, allora le
equazioni di Lagrange sull'insieme W:
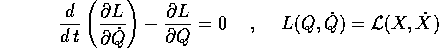
sono equivalenti all'ipotesi che il moto X(t) ha accelerazione
dovuta solo alle forze esterne con energia potenziale  lungo
lo spazio tangente, e subisce reazioni vincolari arbitrarie,
ma nulle nelle direzioni tangenti, in modo da mantenere tutti i
vincoli.
lungo
lo spazio tangente, e subisce reazioni vincolari arbitrarie,
ma nulle nelle direzioni tangenti, in modo da mantenere tutti i
vincoli.
Dimostrazione:
-
-
La dimostrazione del teorema
di covarianza delle equazioni di Lagrange
contiene una formula applicabile anche in questo caso:
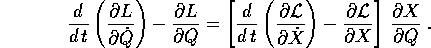
Per effetto delle ipotesi, e del teorema delle funzioni
implicite, la matrice  ha rango massimo
s-g, cioè ha le colonne linearmente indipendenti che
formano una base dello spazio tangente allo spazio delle
configurazioni. Ma allora il vettore dei primi membri delle
equazioni di Lagrange nelle X appartiene allo spazio
ortogonale a questo, cioè
ha rango massimo
s-g, cioè ha le colonne linearmente indipendenti che
formano una base dello spazio tangente allo spazio delle
configurazioni. Ma allora il vettore dei primi membri delle
equazioni di Lagrange nelle X appartiene allo spazio
ortogonale a questo, cioè
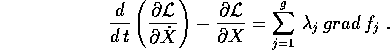
Ora, se la lagrangiana 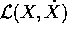 è formata con l'energia
cinetica del sistema e con l'energia potenziale delle forze esterne,
il primo membro dell'equazione rappresenta la differenza tra le forze
percepite dal sistema e le forze esterne (che sarebbe zero, se non ci
fossero vincoli). Perciò l'equazione qua sopra esprime
l'arbitrarietà delle reazioni vincolari nelle direzioni ortogonali
allo spazio tangente, e al tempo stesso che le sole forze esterne sono
presenti nelle direzioni lungo lo spazio tangente.
è formata con l'energia
cinetica del sistema e con l'energia potenziale delle forze esterne,
il primo membro dell'equazione rappresenta la differenza tra le forze
percepite dal sistema e le forze esterne (che sarebbe zero, se non ci
fossero vincoli). Perciò l'equazione qua sopra esprime
l'arbitrarietà delle reazioni vincolari nelle direzioni ortogonali
allo spazio tangente, e al tempo stesso che le sole forze esterne sono
presenti nelle direzioni lungo lo spazio tangente.
C.D.D.Le equazioni di Lagrange per le Q sono in numero minore,
quindi rappresentano delle condizioni più deboli delle equazioni di
Lagrange per le X. Se però supponiamo che il moto sia vincolato,
in modo che i soli valori possibili per le X siano quelli che si
ottengono come immagine delle Q tramite l'applicazione X=X(Q),
allora le equazioni nelle Q sono sufficienti a descrivere il moto.
Le equazioni ``mancanti'' descrivono le reazioni vincolari.
Esempio:
-
- Un pendolo sferico è un corpo puntiforme di massa m,
vincolato a muoversi ad una distanza fissa
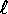 da un
centro, e soggetto ad una forza costante (in direzione ed
intensità); possiamo scegliere gli assi in modo che la forza
sia in direzione delle z negative, e quindi ammetta come
potenziale
da un
centro, e soggetto ad una forza costante (in direzione ed
intensità); possiamo scegliere gli assi in modo che la forza
sia in direzione delle z negative, e quindi ammetta come
potenziale 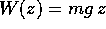 . Lo
spazio delle configurazioni è il
sottoinsieme dello spazio
. Lo
spazio delle configurazioni è il
sottoinsieme dello spazio 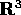 definito da
definito da 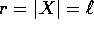 ,
cioè una sfera. Se parametrizziamo la sfera con la
longitudine e la latitudine
,
cioè una sfera. Se parametrizziamo la sfera con la
longitudine e la latitudine
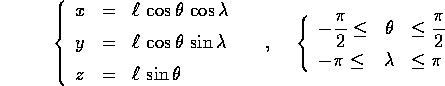
allora possiamo usare il teorema di covarianza per
l'applicazione tra 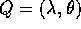 e X=(x,y,z). Le
equazioni di moto saranno ottenute a partire dalla lagrangiana
in coordinate cartesiane
e X=(x,y,z). Le
equazioni di moto saranno ottenute a partire dalla lagrangiana
in coordinate cartesiane
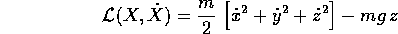
esprimendo la stessa quantità in funzione delle coordinate
polari. Si usano in sostanza le stesse formule che esprimono
le velocità cartesiane nelle
coordinate polari sferiche , salvo che 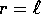 identicamente e
quindi
identicamente e
quindi 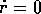 :
:
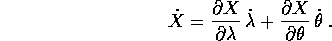
Sostituendo nella lagrangiana 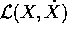 ,
,
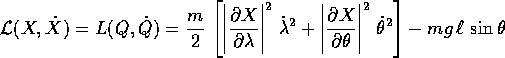
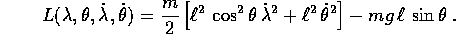
La variabile  è ciclica, quindi una delle due
equazioni di Lagrange asserisce la costanza del momento
coniugato
è ciclica, quindi una delle due
equazioni di Lagrange asserisce la costanza del momento
coniugato 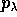 :
:
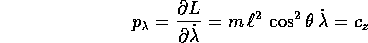
con 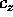 una costante da determinare in base alle condizioni
iniziali. L'altro momento, coniugato a
una costante da determinare in base alle condizioni
iniziali. L'altro momento, coniugato a  , è
, è
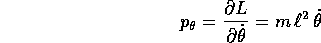
con la sua equazione di Lagrange
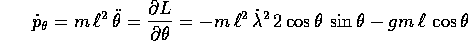
Per sfruttare in la presenza della variabile ciclica
 dobbiamo eliminare la sua velocità
dobbiamo eliminare la sua velocità 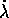 dall'equazione di Lagrange per
dall'equazione di Lagrange per  ; in questo modo
otterremmo un sistema lagrangiano ad un solo grado di
libertà. Questo calcolo è più agevole se si usa
la trasformata di Legendre per passare al sistema hamiltoniano
corrispondente: ricordando la formula della matrice inversa,
si trova immediatamente
; in questo modo
otterremmo un sistema lagrangiano ad un solo grado di
libertà. Questo calcolo è più agevole se si usa
la trasformata di Legendre per passare al sistema hamiltoniano
corrispondente: ricordando la formula della matrice inversa,
si trova immediatamente
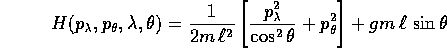
e sostituendo al momento 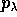 il suo valore costante
il suo valore costante
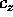 si trova una hamiltoniana ad un grado di libertà con
un parametro:
si trova una hamiltoniana ad un grado di libertà con
un parametro:
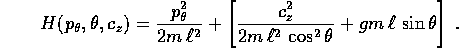
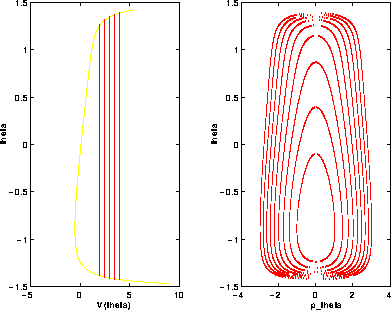
Figure 6.2: Piano delle fasi del pendolo sferico, per un
valore fisso della componente z del momento angolare.
Lo studio qualitativo di questo sistema ad un grado di
libertà è molto semplice: chiamando 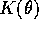 l'energia
potenziale effettiva (l'espressione tra parentesi quadre,
funzione solo di
l'energia
potenziale effettiva (l'espressione tra parentesi quadre,
funzione solo di  e del parametro
e del parametro 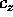 ) i limiti agli estremi
dell'insieme di definizione sono
) i limiti agli estremi
dell'insieme di definizione sono
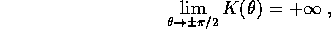
quindi tutti gli insiemi di livello sono compatti. Il solo
punto di equilibrio è in 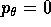 e
e
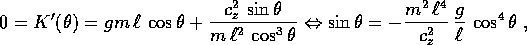
che ha una sola soluzione 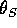 con
con 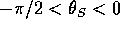 ,
come si può vedere confrontando i grafici dei due membri.
Poiché
,
come si può vedere confrontando i grafici dei due membri.
Poiché 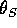 è il solo punto stazionario di
è il solo punto stazionario di
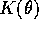 , sarà necessariamente il minimo, quindi un punto
di equilibrio stabile; tutte le altre soluzioni per
, sarà necessariamente il minimo, quindi un punto
di equilibrio stabile; tutte le altre soluzioni per
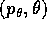 sono periodiche, cioè oscillazioni
attorno a
sono periodiche, cioè oscillazioni
attorno a 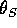 . La soluzione per
. La soluzione per  si trova per
quadratura , a partire dall'equazione di Hamilton per
si trova per
quadratura , a partire dall'equazione di Hamilton per 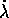 :
:
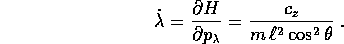
Questa descrizione del moto del pendolo sferico ha soltanto due
``eccezioni'', cioè i punti ai due poli con 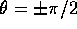 ; in
questi punti la parametrizzazione con
; in
questi punti la parametrizzazione con 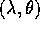 fallisce (la
sua matrice jacobiana non ha rango 2). Si potrebbe naturalmente
utilizzare un'altra carta locale (per esempio con latitudine e
longitudine riferite ad un altro equatore che passa per i poli
dell'altra carta), ma non è necessario. Se il pendolo passa
per uno dei due poli allora
fallisce (la
sua matrice jacobiana non ha rango 2). Si potrebbe naturalmente
utilizzare un'altra carta locale (per esempio con latitudine e
longitudine riferite ad un altro equatore che passa per i poli
dell'altra carta), ma non è necessario. Se il pendolo passa
per uno dei due poli allora 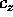 (la componente z del momento
angolare) si annulla ed il moto si svolge lungo un meridiano; in
questo caso possiamo usare la variabile angolo
(la componente z del momento
angolare) si annulla ed il moto si svolge lungo un meridiano; in
questo caso possiamo usare la variabile angolo  come parametro
sul meridiano con
come parametro
sul meridiano con 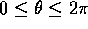 , e la funzione di Hamilton
(la stessa, con
, e la funzione di Hamilton
(la stessa, con 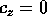 )
)
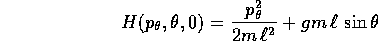
coincide con quella ottenuta nel caso del pendolo piano.
Questo esempio illustra il fatto che un integrale primo
ha esattamente gli stessi effetti di un vincolo: il pendolo sferico
è obbligato a muoversi nel piano per rispettare l'integrale
primo, non perché il movimento solo nel piano faccia parte
della definizione del sistema meccanico.
I due poli 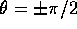 della sfera nell'esempio qua sopra
illustrano un problema che si incontra spesso nella soluzione di
problemi lagrangiani: la presenza di
singolarità isolate
nel sistema di coordinate lagrangiane,
cioè punti dello spazio delle configurazioni per i quali le
coordinate usate non sono lagrangiane, non sono una carta locale. La
parola ``isolate'' va intesa nel senso topologico, cioè esiste un
intorno di ciascuno di questi punti di singolarità in cui non ce ne
sono altri. A questi punti non si può applicare il teorema dei
moti vincolati , perché cade o l'ipotesi di
differenziabilità, o quella che la matrice jacobiana della carta ha
rango massimo, o addirittura la carta locale non è definita. Però
se questi punti singolari sono topologicamente isolati, non è
necessario trovare un'altra carta che li contiene, basta sapere che
esiste. Perciò una soluzione dell'equazione di Lagrange, valida in
tutti i punti tranne che nelle singolarità isolate, potrà passare
per una di queste ed il comportamento della soluzione nel momento di
questo passaggio (per esempio, la velocità) sarà unicamente
determinato per continuità.
della sfera nell'esempio qua sopra
illustrano un problema che si incontra spesso nella soluzione di
problemi lagrangiani: la presenza di
singolarità isolate
nel sistema di coordinate lagrangiane,
cioè punti dello spazio delle configurazioni per i quali le
coordinate usate non sono lagrangiane, non sono una carta locale. La
parola ``isolate'' va intesa nel senso topologico, cioè esiste un
intorno di ciascuno di questi punti di singolarità in cui non ce ne
sono altri. A questi punti non si può applicare il teorema dei
moti vincolati , perché cade o l'ipotesi di
differenziabilità, o quella che la matrice jacobiana della carta ha
rango massimo, o addirittura la carta locale non è definita. Però
se questi punti singolari sono topologicamente isolati, non è
necessario trovare un'altra carta che li contiene, basta sapere che
esiste. Perciò una soluzione dell'equazione di Lagrange, valida in
tutti i punti tranne che nelle singolarità isolate, potrà passare
per una di queste ed il comportamento della soluzione nel momento di
questo passaggio (per esempio, la velocità) sarà unicamente
determinato per continuità.
Così per esempio il punto sulla sfera con 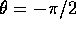 , essendo
un punto di minimo del potenziale, sarà un punto di equilibrio
stabile per il teorema di
stabilità del minimo ,
anche se le equazioni di Lagrange
calcolate qua sopra non valgono in quel punto. Per il teorema delle
funzioni implicite la sfera è una superficie regolare in
ogni suo punto, quindi attorno ai poli esiste un'altra carta in cui si
possono scrivere equazioni di Lagrange che hanno soluzioni
sufficientemente regolari (per esempio,
, essendo
un punto di minimo del potenziale, sarà un punto di equilibrio
stabile per il teorema di
stabilità del minimo ,
anche se le equazioni di Lagrange
calcolate qua sopra non valgono in quel punto. Per il teorema delle
funzioni implicite la sfera è una superficie regolare in
ogni suo punto, quindi attorno ai poli esiste un'altra carta in cui si
possono scrivere equazioni di Lagrange che hanno soluzioni
sufficientemente regolari (per esempio,  rispetto al tempo), il
che rende legittimo completare per continuità le soluzioni mentre
passano dalle singolarità.
rispetto al tempo), il
che rende legittimo completare per continuità le soluzioni mentre
passano dalle singolarità.
Problema
Un pendolo doppio è un sistema di due corpi
puntiformi  di masse
di masse 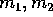 , di cui il primo
è ad una distanza fissa da un centro fisso, il secondo
ad una distanza fissa dal primo:
, di cui il primo
è ad una distanza fissa da un centro fisso, il secondo
ad una distanza fissa dal primo:
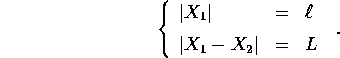
Limitiamoci a considerare un pendolo doppio piano:
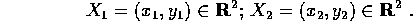
Lo spazio delle configurazioni è il
toro 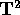 , parametrizzato da due variabili angolo
, parametrizzato da due variabili angolo
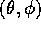 con
con
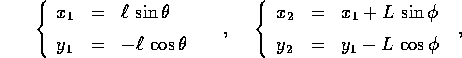
sia nel caso di un moto libero (senza forze esterne), sia nel caso in
cui l'energia
potenziale deriva da un'accelerazione costante in direzione -y,
cioè
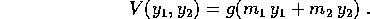
Scrivere la lagrangiana e la hamiltoniana, e determinare le eventuali
posizioni di equilibrio. Nel caso dell'accelerazione costante
dimostrare che la posizione 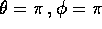 è un punto di
equilibrio stabile.
è un punto di
equilibrio stabile.
Suggerimento: Nel caso con accelerazione costante, il minimo assoluto
dell'energia potenziale si ha quando sia 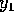 che
che 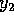 sono minimi;
in tale posizione l'energia è minima, e per il teorema di
stabilità di Lyapounov , o
meglio per la sua diretta conseguenza, il teorema di
stabilità del minimo , si
deve avere un punto di equilibrio stabile; il fatto che il punto di
minimo sia una delle
singolarità isolate
non importa.
sono minimi;
in tale posizione l'energia è minima, e per il teorema di
stabilità di Lyapounov , o
meglio per la sua diretta conseguenza, il teorema di
stabilità del minimo , si
deve avere un punto di equilibrio stabile; il fatto che il punto di
minimo sia una delle
singolarità isolate
non importa.
(Soluzione)
Problema
Sia dato un disco di massa m e raggio R, libero di
ruotare attorno ad un asse perpendicolare al centro Q; il
momento d'inerzia è 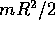 ; supponiamo che il centro
del disco sia libero di muoversi in un piano verticale, ma ad una
distanza costante
; supponiamo che il centro
del disco sia libero di muoversi in un piano verticale, ma ad una
distanza costante 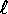 da un punto fisso O. Lo spazio delle
configurazioni è un toro, parametrizzato con l'angolo
da un punto fisso O. Lo spazio delle
configurazioni è un toro, parametrizzato con l'angolo  formato
dalla congiungente OQ con la verticale, e dalla fase di rotazione
del disco. Mostrare che
formato
dalla congiungente OQ con la verticale, e dalla fase di rotazione
del disco. Mostrare che
- (I)
- nel caso in cui non ci siano forze esterne
il sistema descrive un qualsiasi flusso di Kronecker ;
- (II)
- in presenza di accelerazione di gravità costante g,
il moto è descrivibile come prodotto cartesiano del moto di un
pendolo nonlineare e di un rotore libero ;
- (III)
- in presenza di una qualsiasi forza esterna, con energia
potenziale funzione soltanto di
 , il sistema è integrabile.
, il sistema è integrabile.
Il problema qua sopra, l'esempio che lo precede, ed un problema
nella Sezione 6.6, forniscono 5 diversi sistemi
lagrangiani aventi un toro per spazio delle configurazioni; di questi,
4 sono integrabili.




Next: 6.4 SIMMETRIEINTEGRALI PRIMI
Up: 6 SISTEMI CONSERVATIVI: PIÙ
Previous: 6.2 TRASFORMATA DI LEGENDRE
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
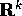 , ma che possono
essere descritti da carte locali con coordinate in
, ma che possono
essere descritti da carte locali con coordinate in 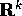 .
Questo si verifica per i moti vincolati di sistemi
composti da più corpi puntiformi, o anche da sistemi estesi
rigidi o parzialmente rigidi. Le equazioni di Lagrange
e di Hamilton possono essere ugualmente impiegate per
descrivere la dinamica, in ciascuna carta locale; le
proprietà globali delle soluzioni possono però richiedere
uno studio attento delle proprietà globali dello spazio
delle configurazioni.
.
Questo si verifica per i moti vincolati di sistemi
composti da più corpi puntiformi, o anche da sistemi estesi
rigidi o parzialmente rigidi. Le equazioni di Lagrange
e di Hamilton possono essere ugualmente impiegate per
descrivere la dinamica, in ciascuna carta locale; le
proprietà globali delle soluzioni possono però richiedere
uno studio attento delle proprietà globali dello spazio
delle configurazioni.
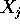 e massa
e massa
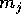 . Allora
. Allora 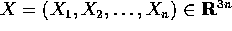 è il
vettore di stato, che esprime la posizione di tutti i corpi.
Gli n corpi avranno un moto vincolato
è il
vettore di stato, che esprime la posizione di tutti i corpi.
Gli n corpi avranno un moto vincolato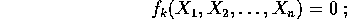
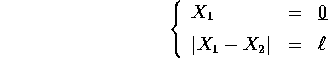
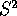 .
.

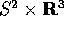 .
.
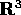 , e non può
essere una sottovarietà di
, e non può
essere una sottovarietà di 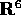 (ma può essere immerso
in
(ma può essere immerso
in 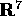 ). Capita spesso che i sistemi con identificazioni, in
cui si passa al quoziente rispetto a qualche simmetria, siano
geometricamente più complessi.
). Capita spesso che i sistemi con identificazioni, in
cui si passa al quoziente rispetto a qualche simmetria, siano
geometricamente più complessi.
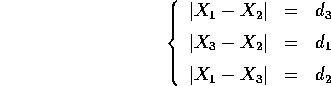
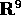 , ma, poiché ci sono 3 vincoli,
il numero di gradi di libertà è 6.
, ma, poiché ci sono 3 vincoli,
il numero di gradi di libertà è 6.
 si può ottenere
una nozione di corpo rigido con una distribuzione continua di
massa; lo spazio delle configurazioni è sempre lo stesso, ma
l'energia cinetica conterrà un termine con il
si può ottenere
una nozione di corpo rigido con una distribuzione continua di
massa; lo spazio delle configurazioni è sempre lo stesso, ma
l'energia cinetica conterrà un termine con il
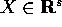 tale che
tale che

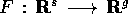 è
un'applicazione di classe
è
un'applicazione di classe  .
Per il teorema delle
.
Per il teorema delle 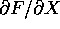 ha rango g in un
punto
ha rango g in un
punto 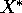 , allora esiste un'applicazione di classe
, allora esiste un'applicazione di classe 
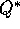 in
in 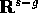 tale che
tale che
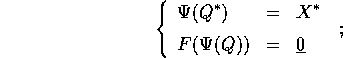
 e di una forza derivante dalle
reazioni vincolari
e di una forza derivante dalle
reazioni vincolari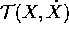 è l'energia
cinetica, il moto del sistema potrà essere studiato, nel senso che
sarà precisato di seguito, per mezzo della funzione di Lagrange
è l'energia
cinetica, il moto del sistema potrà essere studiato, nel senso che
sarà precisato di seguito, per mezzo della funzione di Lagrange
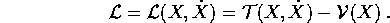
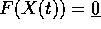 ,
allora la sua velocità soddisfa le condizioni che si ottengono
derivando rispetto al tempo questa equazione, cioè
,
allora la sua velocità soddisfa le condizioni che si ottengono
derivando rispetto al tempo questa equazione, cioè
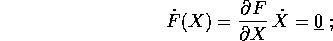
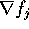 delle
funzioni vincolari
delle
funzioni vincolari 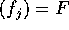 . Lo spazio vettoriale dei
vettori che rispettano questa condizione ha dimensione s-g=b
e si chiama
. Lo spazio vettoriale dei
vettori che rispettano questa condizione ha dimensione s-g=b
e si chiama 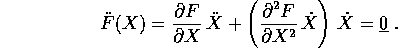
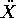 che si trovano nello spazio normale (dei vettori perpendicolari allo
spazio tangente). Ne segue che reazioni vincolari perpendicolari allo
spazio tangente sono sufficienti a garantire il rispetto del vincolo,
e le equazioni di moto saranno della forma
che si trovano nello spazio normale (dei vettori perpendicolari allo
spazio tangente). Ne segue che reazioni vincolari perpendicolari allo
spazio tangente sono sufficienti a garantire il rispetto del vincolo,
e le equazioni di moto saranno della forma
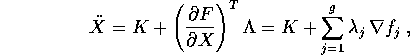
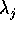 .
.
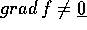 , esiste una carta locale
con due coordinate lagrangiane
, esiste una carta locale
con due coordinate lagrangiane 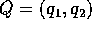 . Se X(t) è
una curva che appartiene alla superficie (identicamente
rispetto a t), allora la sua velocità
. Se X(t) è
una curva che appartiene alla superficie (identicamente
rispetto a t), allora la sua velocità
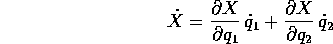
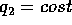 e
e 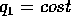 , ed è
ortogonale al gradiente del vincolo:
, ed è
ortogonale al gradiente del vincolo:
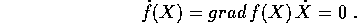
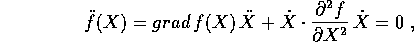
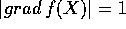 , la forma quadratica in questione è
la
, la forma quadratica in questione è
la 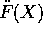 , per velocità
, per velocità 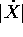 troppo
grandi le reazioni vincolari saranno troppo grandi rispetto alle
proprietà di materiali reali, e il modello dei moti vincolati non
sarà applicabile.
troppo
grandi le reazioni vincolari saranno troppo grandi rispetto alle
proprietà di materiali reali, e il modello dei moti vincolati non
sarà applicabile.
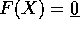 sono i vincoli, allora
sono i vincoli, allora
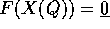 , e derivando rispetto alle coordinate
lagrangiane Q
, e derivando rispetto alle coordinate
lagrangiane Q
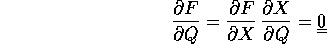

 ha rango massimo b, quindi i vettori
ha rango massimo b, quindi i vettori 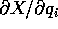 sono una base dello spazio tangente. Questo è il punto
critico nella dimostrazione che è possibile utilizzare il
formalismo lagrangiano per i moti vincolati (se i vincoli sono lisci).
sono una base dello spazio tangente. Questo è il punto
critico nella dimostrazione che è possibile utilizzare il
formalismo lagrangiano per i moti vincolati (se i vincoli sono lisci).
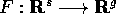 (di classe
(di classe
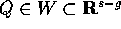 sono le coordinate lagrangiane di una carta locale, allora le
equazioni di Lagrange sull'insieme W:
sono le coordinate lagrangiane di una carta locale, allora le
equazioni di Lagrange sull'insieme W:
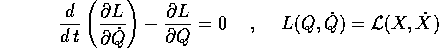
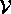 lungo
lo spazio tangente, e subisce
lungo
lo spazio tangente, e subisce 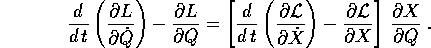
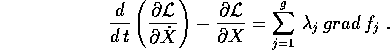
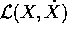 è formata con l'energia
cinetica del sistema e con l'energia potenziale delle forze esterne,
il primo membro dell'equazione rappresenta la differenza tra le forze
percepite dal sistema e le forze esterne (che sarebbe zero, se non ci
fossero vincoli). Perciò l'equazione qua sopra esprime
l'arbitrarietà delle reazioni vincolari nelle direzioni ortogonali
allo spazio tangente, e al tempo stesso che le sole forze esterne sono
presenti nelle direzioni lungo lo spazio tangente.
è formata con l'energia
cinetica del sistema e con l'energia potenziale delle forze esterne,
il primo membro dell'equazione rappresenta la differenza tra le forze
percepite dal sistema e le forze esterne (che sarebbe zero, se non ci
fossero vincoli). Perciò l'equazione qua sopra esprime
l'arbitrarietà delle reazioni vincolari nelle direzioni ortogonali
allo spazio tangente, e al tempo stesso che le sole forze esterne sono
presenti nelle direzioni lungo lo spazio tangente.
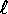 da un
centro, e soggetto ad una forza costante (in direzione ed
intensità); possiamo scegliere gli assi in modo che la forza
sia in direzione delle z negative, e quindi ammetta come
potenziale
da un
centro, e soggetto ad una forza costante (in direzione ed
intensità); possiamo scegliere gli assi in modo che la forza
sia in direzione delle z negative, e quindi ammetta come
potenziale 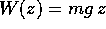 . Lo
spazio delle configurazioni è il
sottoinsieme dello spazio
. Lo
spazio delle configurazioni è il
sottoinsieme dello spazio 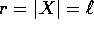 ,
cioè una sfera. Se parametrizziamo la sfera con la
longitudine e la latitudine
,
cioè una sfera. Se parametrizziamo la sfera con la
longitudine e la latitudine
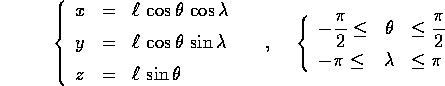
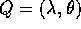 e X=(x,y,z). Le
equazioni di moto saranno ottenute a partire dalla lagrangiana
in coordinate cartesiane
e X=(x,y,z). Le
equazioni di moto saranno ottenute a partire dalla lagrangiana
in coordinate cartesiane
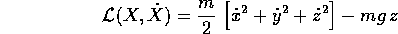
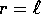 identicamente e
quindi
identicamente e
quindi 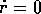 :
:
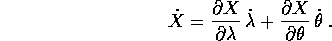
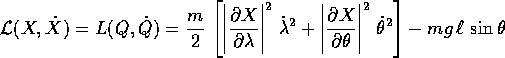
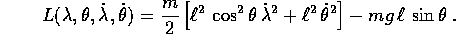
 è ciclica, quindi una delle due
equazioni di Lagrange asserisce la costanza del momento
coniugato
è ciclica, quindi una delle due
equazioni di Lagrange asserisce la costanza del momento
coniugato 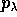 :
:
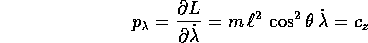
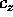 una costante da determinare in base alle condizioni
iniziali. L'altro momento, coniugato a
una costante da determinare in base alle condizioni
iniziali. L'altro momento, coniugato a  , è
, è
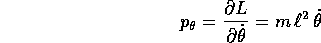
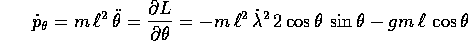
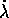 dall'equazione di Lagrange per
dall'equazione di Lagrange per 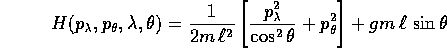
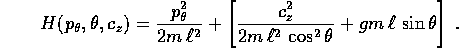

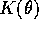 l'energia
potenziale effettiva (l'espressione tra parentesi quadre,
funzione solo di
l'energia
potenziale effettiva (l'espressione tra parentesi quadre,
funzione solo di 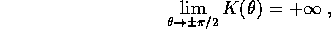
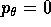 e
e
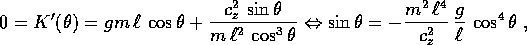
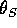 con
con 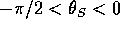 ,
come si può vedere confrontando i grafici dei due membri.
Poiché
,
come si può vedere confrontando i grafici dei due membri.
Poiché  sono periodiche, cioè oscillazioni
attorno a
sono periodiche, cioè oscillazioni
attorno a 
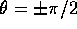 ; in
questi punti la parametrizzazione con
; in
questi punti la parametrizzazione con 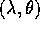 fallisce (la
sua matrice jacobiana non ha rango 2). Si potrebbe naturalmente
utilizzare un'altra carta locale (per esempio con latitudine e
longitudine riferite ad un altro equatore che passa per i poli
dell'altra carta), ma non è necessario. Se il pendolo passa
per uno dei due poli allora
fallisce (la
sua matrice jacobiana non ha rango 2). Si potrebbe naturalmente
utilizzare un'altra carta locale (per esempio con latitudine e
longitudine riferite ad un altro equatore che passa per i poli
dell'altra carta), ma non è necessario. Se il pendolo passa
per uno dei due poli allora 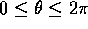 , e la funzione di Hamilton
(la stessa, con
, e la funzione di Hamilton
(la stessa, con 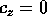 )
)
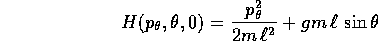
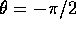 , essendo
un punto di minimo del potenziale, sarà un punto di equilibrio
stabile per il teorema di
, essendo
un punto di minimo del potenziale, sarà un punto di equilibrio
stabile per il teorema di
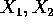 di masse
di masse 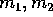 , di cui il primo
è ad una distanza fissa da un centro fisso, il secondo
ad una distanza fissa dal primo:
, di cui il primo
è ad una distanza fissa da un centro fisso, il secondo
ad una distanza fissa dal primo:
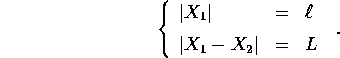
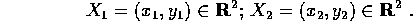
 , parametrizzato da due variabili angolo
, parametrizzato da due variabili angolo
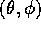 con
con
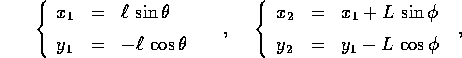
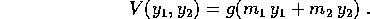
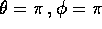 è un punto di
equilibrio stabile.
è un punto di
equilibrio stabile.
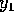 che
che 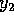 sono minimi;
in tale posizione l'energia è minima, e per il teorema di
sono minimi;
in tale posizione l'energia è minima, e per il teorema di
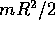 ; supponiamo che il centro
del disco sia libero di muoversi in un piano verticale, ma ad una
distanza costante
; supponiamo che il centro
del disco sia libero di muoversi in un piano verticale, ma ad una
distanza costante