Sommario La stabilità di un punto di equilibrio può essere determinata mediante le proprietà di una funzione di Lyapounov, che generalizza le proprietà della distanza nell'intorno di un pozzo e dell'energia in un sistema dissipativo.
Consideriamo un sistema dinamico continuo
con il campo vettoriale F definito e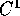 
su di un aperto 
.
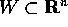Definizione:
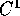in W, si dice
derivata totale di V (rispetto al campo vettoriale F(X))
la funzione:
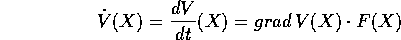
Se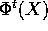 
è il flusso integrale di F(X), per il
teorema di derivazione delle funzioni composte la derivata totale
è la derivata in t=0 della funzione di t ottenuta fissando la
condizione iniziale:
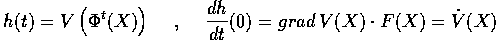
La notazione con il punto è consistente
con quella già adottata per il vettore X stesso: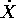 
è
anche una derivata totale.
La derivata totale esprime la variazione nel tempo di una funzione, e può essere utilizzata sia per calcoli quantitativi che per studiare le proprietà qualitative come la stabilità.
Definizione:
in un intorno U di 
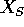(si intende che 
)
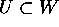si dice funzione di Lyapounov per l'equilibrio 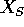se
valgono le due condizioni:
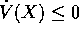per ogni X in U.
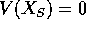e V(X)>0 per ogni X in U escluso .
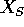La funzione di Lyapounov ha un minimo in corrispondenza del punto di equilibrio (per convenienza si fissa il valore del minimo a zero), e derivata totale mai positiva al di fuori del minimo, quindi il valore della funzione non cresce lungo le soluzioni.
Esempio:
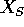un pozzo : come visto nella dimostrazione del
teorema del pozzo nonlineare esiste una norma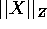 
,
associata ad una base Z dei vettori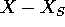 
, tale che:
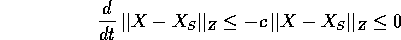
per ogni X in un intorno U di 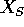, e con -c una costante
negativa. Perciò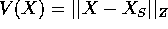 
è una funzione di Lyapounov.
Teorema di stabilità di Lyapounov :
Se il punto di equilibrio 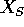possiede, in un intorno U, una
funzione di Lyapounov V(X), allora è stabile . Se inoltre
esiste un intorno U di 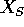in cui vale anche:
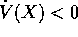per ogni X in U escluso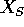
allora 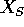è anche asintoticamente stabile .
Se valgono (b) e (c) si parla di funzione di Lyapounov stretta .
Dimostrazione:
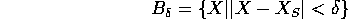
il cui bordo è la sfera
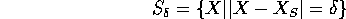
con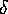 
abbastanza piccolo perché sia 
,
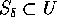quindi anche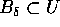 
. Poiché 
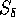è un
compatto , esiste il minimo m di V(X) su 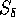, e
vale m>0. Consideriamo l'insieme Q definito da:
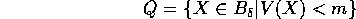
Allora le soluzioni che partono da una condizione iniziale X in
Q non possono mai passare da un punto di 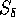, perché su
di esse il valore iniziale di V è minore di m, e la funzione
V non può crescere lungo l'orbita. Ma una curva continua non
può uscire da un insieme limitato senza passare per la sua
frontiera . Perciò l'intorno Q è tale che le soluzioni
che vi iniziano non escono da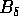 
.
Poiché questo è vero per tutti i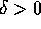 
abbastanza piccoli,
gli insiemi 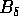sono un
sistema fondamentale di intorni ,
e la definizione di stabilità è soddisfatta.
Se vale anche (c), la funzione di Lyapounov stretta diminuisce lungo
le soluzioni. Allora prendiamo una condizione iniziale nell'insieme
Q di cui sopra; la soluzione X(t) non può lasciare ,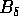
cioè è limitata per t>0. Quindi esiste almeno un valore limite
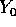contenuto nella chiusura di 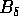, che è un
compatto . Sia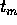 
una successione di valori di t, con
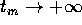per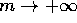 
, tale che
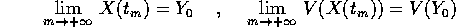
(la prima per definizione di valore limite, la seconda per la
continuità della funzione V). Se però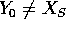 
esiste una
soluzione Y(t) che ha per condizione iniziale 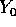, lungo la quale
V(Y(t)) è strettamente decrescente, avendo per (c) derivata negativa:
quindi per s>0,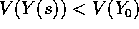 
.
Se allora scegliamo un m abbastanza grande, in modo che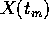 
sia abbastanza vicino ad 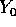, per la continuità del flusso
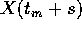sarà abbastanza vicino ad Y(s), per il teorema di
permanenza del segno la funzione continua V soddisferà a
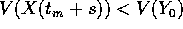. Ma allora la soluzione X(t) per 
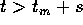non può ripassare arbitrariamente vicino a 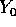, perché questo
contraddice la decrescenza di V(X(t)). Ne segue che 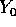non
può essere un valore limite ed essere diverso da 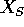. Quindi
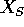è attrattivo.
Esempio:
:
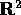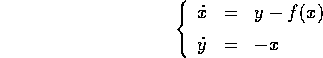
(equazione di Lienard ). Se prendiamo una funzione f(x)
dispari e positiva per x>0, per esempio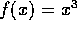 
, l'origine è
stabile. Infatti possiamo usare come funzione di Lyapounov
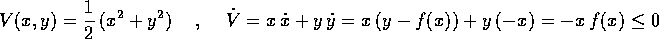
L'origine, in questo esempio, è anche asintoticamente stabile, benché non valga la proprietà (c). Per dimostrarlo però bisogna usare il successivo teorema della funzione di Lyapounov decrescente .
Esercizio Studiare la stabilità dell'origine per il sistema
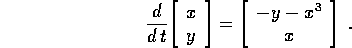
Il teorema di stabilità di Lyapounov consente di trarre delle conclusioni sulla stabilità senza conoscere esplicitamente le soluzioni. D'altro canto non esiste un procedimento automatico valido in tutti i casi per fabbricare le funzioni di Lyapounov, a parte il caso dei pozzi in cui il comportamento qualitativo è già noto. Le funzioni di Lyapounov sono spesso suggerite dall'interpretazione fisica del sistema dinamico, per esempio in termini di energia .