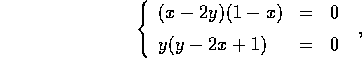
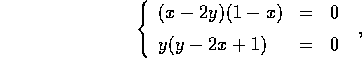
e si studiano linearizzando F nei punti determinati. Si ottengono così i sistemi 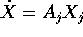 per le coppie
per le coppie
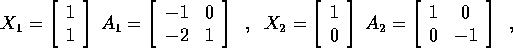
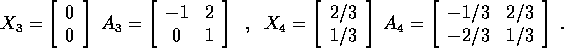
Solamente 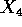 è una sorgente, mentre gli altri tre punti sono selle nonlineari : gli autovalori corrispondenti sono infatti
è una sorgente, mentre gli altri tre punti sono selle nonlineari : gli autovalori corrispondenti sono infatti
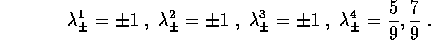
Si noti che il sistema è conservativo , anzi hamiltoniano con 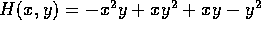 .
.
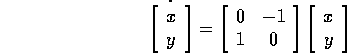
gli autovalori sono immaginari puri, ed è necessario cercare una funzione di Lyapounov V(x,y) per l'origine. Ha successo il tentativo 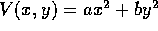 , con
, con 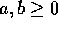 : affinché
: affinché 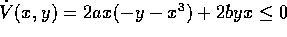 basta che a=b.
basta che a=b.
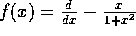
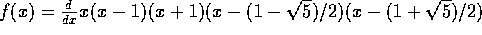
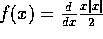
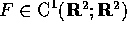 e
e 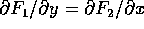 , su ogni componente semplicemente connessa D del dominio di F (in tal caso tutto
, su ogni componente semplicemente connessa D del dominio di F (in tal caso tutto 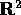 )è possibile determinare V(x) in modo che F=grad -V(x): integrando su una curva
)è possibile determinare V(x) in modo che F=grad -V(x): integrando su una curva 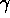 che congiunge
che congiunge 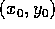 e (x,y) in D, (per esempio
e (x,y) in D, (per esempio 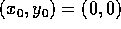 e
e 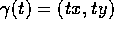 ) si ottiene
) si ottiene 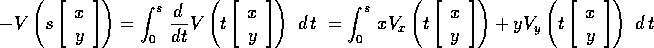
quindi, per s=1,  . In questo caso, il sistema è gradiente con
. In questo caso, il sistema è gradiente con 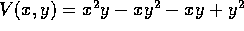 ; i punti critici sono
; i punti critici sono
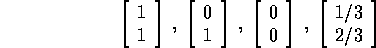
(tre selle ed una sorgente).