Soluzioni del capitolo 4

ESERCIZIO 4.1   In termini della matrice compagna A dell'equazione, il problemi hanno soluzione

1. calcolando la forma canonica di A, risulta

   

   

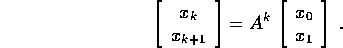
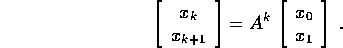
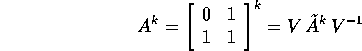
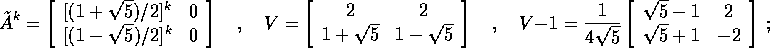
   quindi la serie di Fibonacci è calcolabile con

   

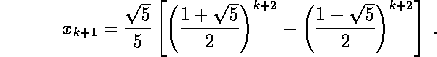
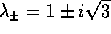2. Gli autovalori di

   

   sono complessi, e la forma canonica di A è la rappresentazione matriciale di 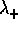rispetto alla base costituita da parte reale e parte immaginaria di un autovettore di :

   

   

   

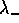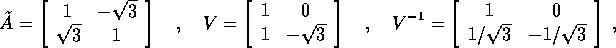
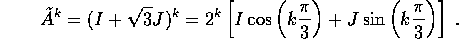
   Allora

   

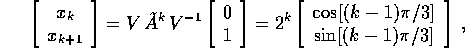
   e le orbite non sono in genere limitate.

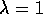3. La molteplicità dell'unico autovalore di A è 2, e risulta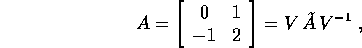

   

   

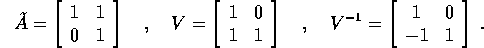
   Per 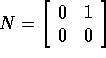si calcola 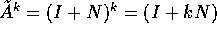, ovvero

   

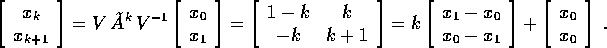
   Le orbite sono "rettilinee" se 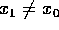: i punti della bisettrice sono punti fissi della mappa.

ESERCIZIO 4.2  Il sistema dinamico discreto è:

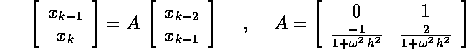
con gli autovalori di A:

che sono gli inversi di quelli che si ottengono con le differenze in avanti. Perciò le soluzioni del sistema discretizzato decrescono come 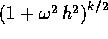e tendono a 0 per .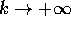