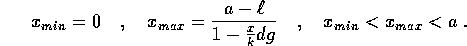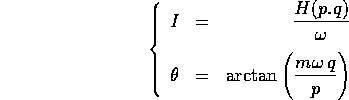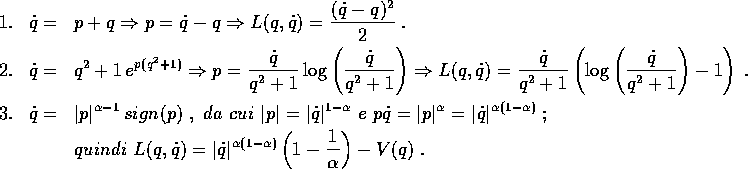
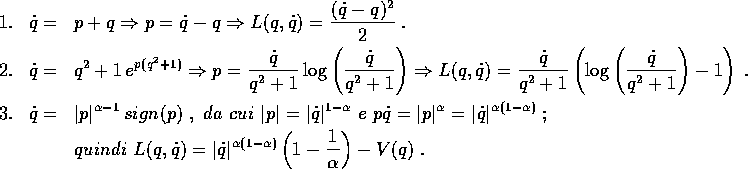
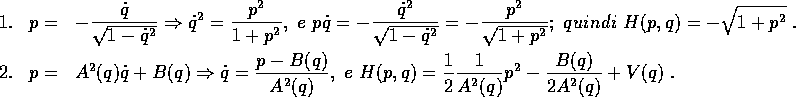
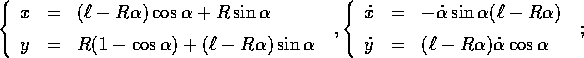
le energie cinetica e potenziale sono date da
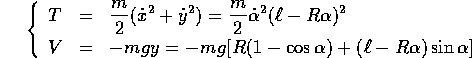
e dalla lagrangiana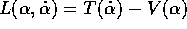 
si ottiene, per
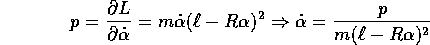
la hamiltoniana H=T+V
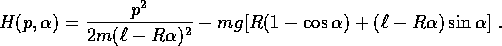
Intorno al punto di equilibrio stabile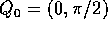 
, H ha la forma
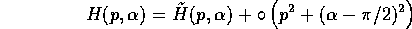
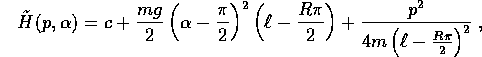
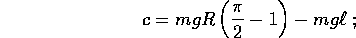
approssimando le piccole oscillazioni intorno a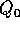 
con quelle del sistema (lineare) con hamiltoniana 
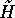, si ottengono ellissi (le curve di livello 
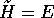) del tipo
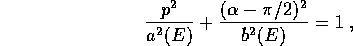
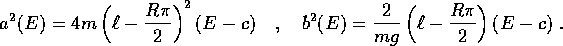
Nell'approssimazione scompare la dipendenza del periodo dall'energia:
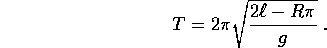
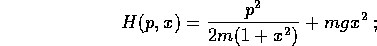
il periodo delle oscillazioni di energia E intorno al vertice della parabola risulta
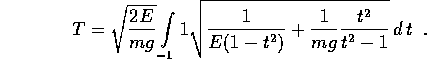
Nel secondo caso, il periodo risulta
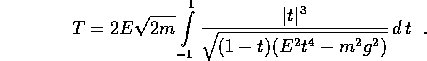
le curve di livello sono limitate per E<0, illimitate per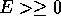 
. Nel primo caso l'orbita ricade sulla superficie z=R dopo un tempo finito, nel secondo va all'infinito. La funzione energia è
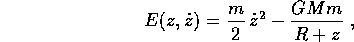
quindi la velocità iniziale critica che separa i due casi è
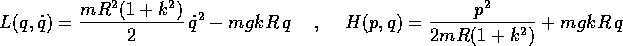
L'equazione di Lagrange è
con secondo membro costante, quindi le soluzioni sono funzioni quadratiche del tempo.
: 
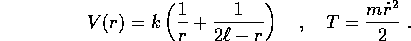
Dunque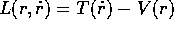 
e, per 
,
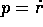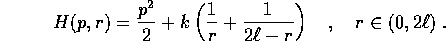
Il periodo dipende da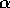 
tramite un integrale ellittico:
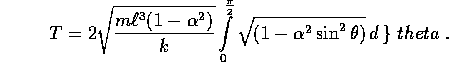
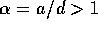, la forza agente sul cubo è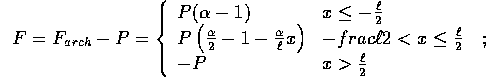 
la lagrangiana e l'hamiltoniana sono
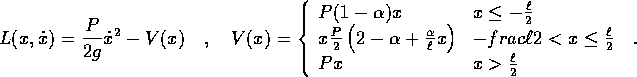
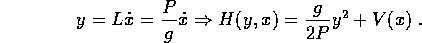
Il punto di equilibrio si trova in corrispondenza di
(la sua posizione rispetto al pelo del liquido dipende dal rapporto 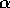fra la sua densità e quella del solido). La traiettoria passante per 
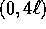ha energia 
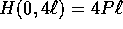; l'altra sua intersezione con l'asse x è la condizione iniziale richiesta:
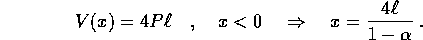
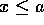(non si consente alla molla di superare il ciglio dello strapiombo). L'energia potenziale è data da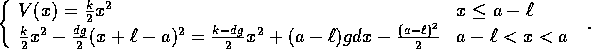 
Nelle ipotesi date, il potenziale ha un minimo ed un massimo relativo (ed il sistema un centro ed una sella, per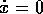 
) rispettivamente in
