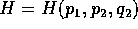Sommario Un sistema hamiltoniano a due gradi di libertà, con un altro integrale primo indipendente dalla hamiltoniana, è sempre integrabile mediante quadrature ed inversioni. Questo può essere dimostrato sotto ipotesi molto generali; in casi abbastanza semplici, come quello delle geodetiche sulle superfici di rivoluzione, le formule risolutive sono di facile scrittura. Perché un sistema ad n gradi di libertà sia integrabile occorrono non solo n integrali primi indipendenti, ma anche ipotesi più restrittive, come quella che le parentesi di Poisson degli integrali siano nulle.
Consideriamo una hamiltoniana a due gradi di libertà. In generale
non è detto che sia possibile esprimerne le soluzioni in modo
analitico, cioè con manipolazioni algebriche, quadrature ed
inversioni; in effetti la maggior parte delle hamiltoniane sono
non integrabili .
Sono integrabili, come abbiamo visto in
molti esempi, le hamiltoniane che hanno una variabile ciclica, del tipo
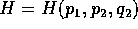, per le quali
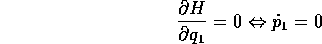
e, sostituendo a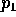 
il suo valore costante, si ottiene una
hamiltoniana ad un grado di libertà con parametro. Se però si
conosce una hamiltoniana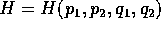 
che dipende
effettivamente da quattro variabili,
come si può scoprire se esiste un cambiamento di variabili
canonico che fa apparire una variabile ciclica? Questo problema di
integrabilità può essere ridotto in un altra forma assai più
espressiva.
Supponiamo che il sistema ammetta un integrale primo G(P,Q). Il
calcolo della derivata totale 
può essere eseguito mediante
la parentesi di Poisson
poiché 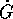è la derivata di G lungo il flusso del sistema
definito da H:
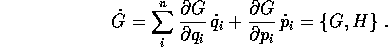
Le parentesi di Poisson hanno molte proprietà importanti, ma la più semplice è
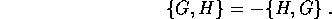
Allora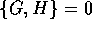 
implica 
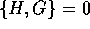(e viceversa), e se esiste un
integrale primo G(P,Q), anche H((P,Q)) è costante lungo il flusso di
G, il quale è perciò un gruppo ad un parametro che
lascia invariata la hamiltoniana. Questo è praticamente
l'inverso del teorema di Noether .
Se il sistema di hamiltoniana H(P,Q) ammette un integrale primo
G((P,Q)), esiste un gruppo ad un parametro di simmetrie; se allora si
potessero parametrizzare le orbite del sistema dinamico definito da
G(P,Q) con una coordinata, questa sarebbe una coordinata ciclica per
H. Per esempio, se G è un integrale del tipo del momento
angolare, esiste una variabile angolo 
tale che
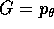. In altri casi, non è affatto ovvio quale possa essere
la variabile ciclica. È inoltre chiaro che la relazione tra G ed
H non deve essere banale: per esempio, se G=f(H) (con f una
qualsiasi funzione 
), sarà sempre vero che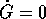 
, ma la
conoscenza di G non fornisce alcuna informazione supplementare alla
conoscenza di H.
Teorema di Arnold-Jost :
Sia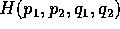 
una hamiltoniana a due gradi di libertà,
di classe 
su di un aperto W. Sia 
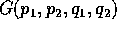un
integrale primo pure di classe :
funzionalmente indipendente
da H, cioè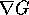 
è
linearmente indipendente da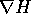 
in ogni punto di W. Siano
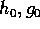due numeri reali tali che l'insieme di livello 
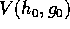di
equazioni
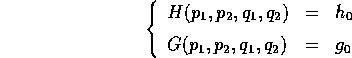
è compatto in W. Allora:
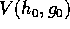è invariante per il flusso di H,
e le sue componenti connesse sono
tori bidimensionali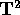 
.
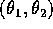che
forniscono una carta del toro 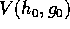, tali che il flusso
integrale di H ristretto a 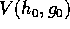è un
flusso di Kronecker :
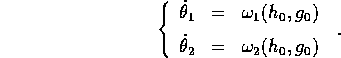
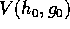su cui è definita
una trasformazione canonica
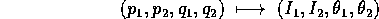
in cui le variabili azione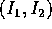 
sono
funzioni soltanto dei valori di G ed H, e
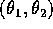sono variabili angolo.
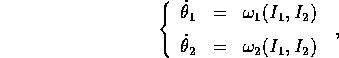
cioè è ancora un flusso di Kronecker in cui ciascuna
frequenza propria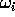 
è funzione delle sole
variabili azione.
L'aperto W può essere contenuto in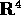 
, oppure, in
presenza di variabili angolo tra le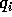 
, si può anche avere
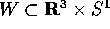oppure 
.
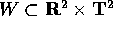Dimostrazion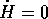e:
e 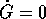. Per il teorema delle
funzioni implicite , ogni insieme V(h,g) è comunque
una varietà differenziabile di dimensione 2. Inoltre
tali varietà
compatte di dimensione 2 sono ``pettinabili'', cioè ammettono
campi vettoriali tangenti che
non si annullano mai: per esempio,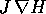 
(e 
). Per la teoria della
caratteristica di Eulero-Poincaré la sola varietà bidimensionale che può
essere ``pettinata'' in
questo senso è il toro .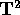
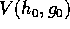è invariante per i due flussi
integrali, quello definito dalla hamiltoniana H con variabile
indipendente t (il tempo), e quello definito dalla hamiltoniana
G con un'altra variabile indipendente s (che non ha il
significato di tempo). Perciò 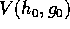si può descrivere
come quoziente di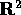 
rispetto all'azione di un gruppo a due
parametri (t,s). La chiave della dimostrazione consiste nel
mostrare che l'insieme dei punti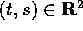 
che lasciano
fisso un dato punto del toro è un sottogruppo discreto (il
sottogruppo di isotropia del punto dato) di 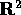, quindi
ha esattamente due generatori. Le variabili angolo 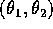sono semplicemente le coordinate in 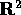rispetto a
questi due generatori (divise per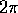 
).
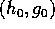, ed in modo
differenziabile rispetto a (h,g). Le variabili azione sono
definite da
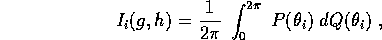
dove la curva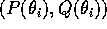 
sul toro si ottiene
variando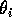 
in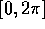 
e lasciando fisse l'altra variabile
angolo, g ed h. Per la dimostrazione che la
trasformazione così definita è canonica, si veda
[Arnold 86], capitolo 10.
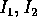sono solo funzione di h,g, allora H
scritta nelle variabili azione-angolo è funzione solo delle
variabili azione:
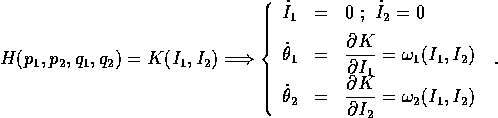
Perciò il sistema è risolubile, nelle nuove variabili, mediante soli scorrimenti , che sono flussi di Kronecker sui tori invarianti.
L'integrale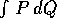 
appare anche nel metodo di
Hamilton-Jacobi; infatti una funzione definita da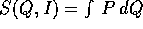 
dove l'integrale deve essere eseguito sulla superficie I=cost è
una funzione caratteristica di Hamilton-Jacobi . La
dimostrazione del teorema di Arnold-Jost chiarisce che questo
integrale non è una semplice quadratura nello spazio delle
Q, ma l'integrale di linea della
forma differenziale lineare
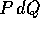. Le scelte di segni nel metodo della
separazione delle variabili possono essere spiegate in
termini di due lembi del toro invariante che si proiettano sullo
stesso insieme nello spazio delle Q.
Una classe importante di problemi a due gradi di libertà, ma che sono risolubili per quadratura, perché hanno un integrale primo funzionalmente indipendente dalla hamiltoniana, si ottiene considerando dei moti vincolati a superfici, senza forze esterne.
Consideriamo una superficie di rivoluzione : se l'asse di
simmetria è assunto come asse z, allora in coordinate polari
cilindriche (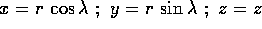 
)
l'equazione della superficie è della forma f(r,z)=0. Se
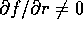, allora si potrà localmente ricavare
r=r(z), per cui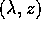 
sarà un sistema di
coordinate lagrangiane per la superficie:
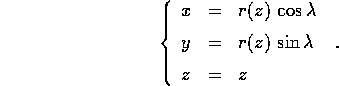
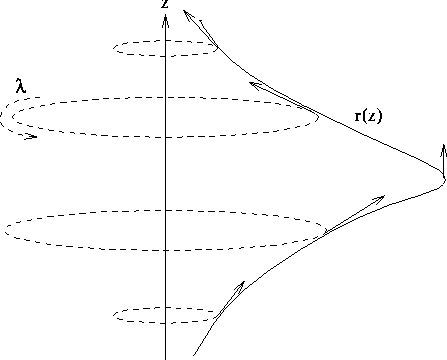
Figure 6.3: Superficie di rivoluzione ottenuta facendo
ruotare la curva r=r(z) attorno all'asse z. I vettori indicati sono
le derivate rispetto a z, mentre quelle rispetto all'angolo di
rotazione sono tangenti ai paralleli (tratteggiati).
Lo spazio tangente sarà generato dai vettori
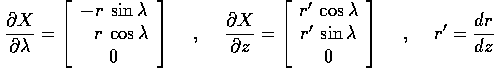
le cui proprietà metriche sono:
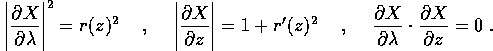
La superficie è regolare, se f è di classe , nei punti
in cui r> 0.
In assenza di forze esterne, il moto di un corpo puntiforme di massa m vincolato alla superficie sarà quindi deducibile dalla lagrangiana ridotta alla sola energia cinetica
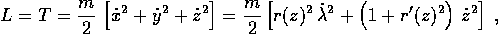
i cui momenti sono
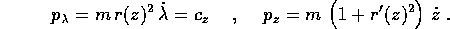
Il momento coniugato alla longitudine 
è un integrale
primo, che coincide con la componente z del momento angolare (sulla
quale le reazioni vincolari non influiscono). Eseguendo la trasformata
di Legendre si trova la hamiltoniana
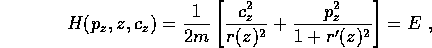
che definisce un sistema hamiltoniano ad un grado di libertà con
parametro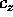 
. La soluzione può quindi essere espressa mediante
quadrature ed inversioni a partire dalla formula
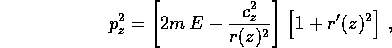
che può anche essere impiegata per lo studio qualitativo delle
soluzioni. Se è limitato l'insieme U dei valori di z, per i quali
il secondo
membro dell'equazione qui sopra è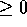 
,
allora a ciascun intervallo di U corrisponde un toro invariante
nello spazio delle fasi. Per esempio, supponiamo che
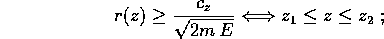
allora ad ogni valore di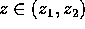 
corrispondono due valori di
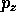, uno positivo ed uno negativo, sempre con lo stesso valore
degli integrali primi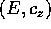 
; invece a 
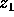ed a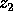 
corrisponde solo 
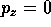. Questo definisce un insieme
equivalente ad una circonferenza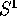 
, che è la traiettoria di
un'orbita periodica del sistema hamiltoniano ad un grado di
libertà definito da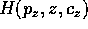 
. Usando una coppia
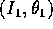di variabili azione-angolo per
parametrizzare una corona circolare di simili orbite periodiche
(sempre con costante ma con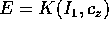 
variabile),
si trova che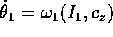 
, cioè ogni 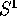è
percorso con frequenza costante.
Però nello spazio delle fasi del problema originale c'è anche la
variabile , che è ciclica, e può essere quindi espressa
per quadratura a partire dalla soluzione per l'altra variabile z:
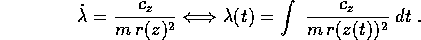
Il toro di livello definito da 
è quindi
parametrizzato dalle due variabili angolo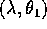 
. Il
teorema di Arnold-Jost assicura che
esiste il modo di definire un'altra coppia di variabili canoniche
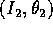, in modo tale ch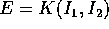e 
e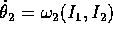 
. Sfruttando il fatto che è
ciclica, si può supporre che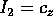 
; però 
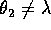, anche se le due variabili hanno la stessa frequenza media,
cioè compiono un giro in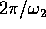 
.
Gli esercizi e problemi che seguono sono casi particolari di questo problema integrabile, detto delle geodetiche sulle superfici di rivoluzione.
Il nome di geodetiche fa riferimento ad una proprietà delle curve che risolvono questo problema, e più in generale delle soluzioni di un problema di moto vincolato con L=T. Le soluzioni sono anche punti stazionari del funzionale
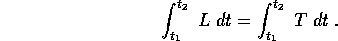
Questo principio variazionale può essere ricondotto, con alcuni passaggi, alla stazionarietà dell'integrale che esprime la lunghezza della curva soluzione. Perciò le geodetiche sono curve di lunghezza stazionaria, tra quelle vincolate a restare sulla varietà delle configurazioni; per intervalli di tempo abbastanza corti si può dimostrare che la lunghezza è in effetti minima. Per una trattazione delle equazioni di Lagrange dedotto dal principio variazionale si può consultare [Arnold 86], capitoli 3 e 4.
Esercizio Il cilindro è dato da r=R costante, r'=0. Determinare le geodetiche. (Soluzione)
Problema Un iperboloide ad una falda di rivoluzione è dato da
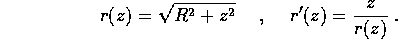
Un iperboloide a due falde di rivoluzione è dato da
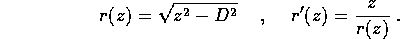
Trovare le geodetiche nei due casi; dire se formino tori invarianti nello spazio delle fasi. (Soluzione)
Problema Data la superficie di rivoluzione
dimostrare che tutte le geodetiche sono limitate, quindi
appartengono a tori invarianti, ad eccezione del caso in cui
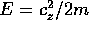(allorché i tori invarianti degenerano in una
circonferenza).
Non è sempre vero che il sistema di coordinate lagrangiano
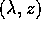sia il più conveniente. Poiché l'esplicitazione
r=r(z) della relazione implicita f(r,z)=0 vale solo
localmente, ci sono casi in cui una diversa parametrizzazione della
curva f(r,z)=0 è più conveniente, per esempio perché può
fornire una unica carta per tutta la superficie.
Esempio:
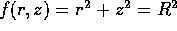, in luogo di
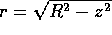si può usare la parametrizzazione mediante
latitudine e longitudine
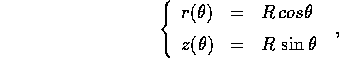
che conduce alla formula del momento
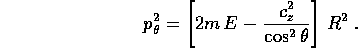
Supponiamo allora di avere un pendolo sferico senza forza esterna.
Tutte le soluzioni sono limitate e formano dei tori invarianti, ad
eccezione di quelle con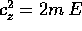 
e quelle con 
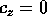; queste
ultime passano dai punti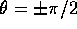 
, e dovrebbero essere trattate a
parte. È comunque facile vedere che in questi casi eccezionali i
tori di livello degenerano in circonferenze.
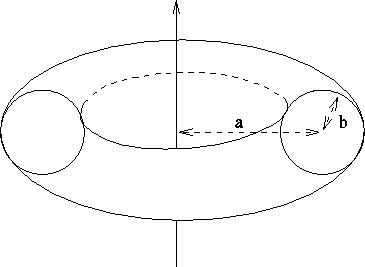
Figure 6.4: Un toro considerato come superficie di
rivoluzione: una circonferenza di raggio b ruota attorno ad un asse
posto ad una distanza a dal suo centro.
Problema Dato il toro di equazioni
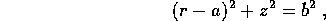
con a>b>0, descriverne le geodetiche.
Suggerimento: Usare la parametrizzazione
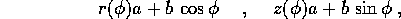
che descrive con una sola carta tutto il toro ed è ovunque regolare per a>b>0.
La generalizzazione del teorema di Arnold-Jost ad un numero qualsiasi di gradi di libertà richiede di tenere conto di un problema aggiuntivo, quello della commutazione tra gli integrali.
Sia data una hamiltoniana H(P,Q) ad n gradi di libertà, ossia con
(P,Q) in un aperto W che appartiene ad 
(o magari a
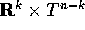), e supponiamo di avere tanti integrali primi
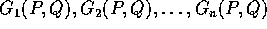quanti sono i gradi di libertà
(possiamo supporre che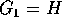 
, visto che la hamiltoniana è un
integrale primo). Valgono allora le relazioni contenenti le
parentesi di Poisson :
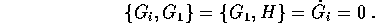
Tuttavia, non necessariamente valgono anche le
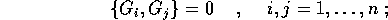
quando ciò accade, cioè se si annullano tutte le parentesi di Poisson tra gli integrali due a due, allora diciamo che gli integrali sono in commutazione .
Esempio:
, posizioni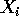 
,
e momenti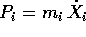 
,
consideriamo il vettore momento angolare
e le sue componenti secondo gli assi (x,y,z), che indichiamo con
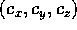. Le parentesi di Poisson tra queste tre
funzioni scalari non sono nulle: per esempio,
come si può calcolare direttamente esprimendo i prodotti vettori in componenti.
Il secondo problema è costituito dall'elevata dimensione dello spazio
delle fasi, che potrebbe far temere una grande complicazione nella
struttura delle varietà di livello: con n integrali primi
in uno spazio delle fasi di dimensione 2n, ci aspettiamo che gli
insiemi di livello siano varietà di dimensione 2n-n=n. In realtà
l'unico tipo di varietà di dimensione n che occorre considerare
è il toro
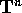, che è il prodotto cartesiano di n copie
della circonferenza 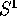(la varietà parametrizzata da una
sola carta con n variabili angolo).
Teorema di Arnold-Jost :
Sia H(P,Q) una hamiltoniana, di classe su un aperto W dello
spazio delle fasi, e siano 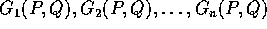delle
funzioni che formano un sistema di n integrali
funzionalmente indipendenti ed in commutazione . Se
V(G) è l'insieme di livello di equazioni
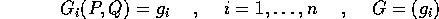
ed è compatto e connesso, allora è un toro 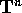, ed esiste un
intorno U di V(G) in W su cui è definito un cambiamento di
coordinate canonico
le n variabili angolo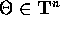 
parametrizzano i tori
di livello, mentre le variabili azione I sono funzione solo dei
valori G degli
integrali primi. In particolare, H(P,Q)=K(I): il
sistema è perciò risolubile mediante scorrimenti, con le variabili
angolo che cambiano linearmente rispetto al tempo secondo l'equazione
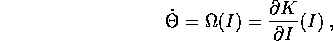
dove le frequenze proprie
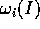dipendono dalle sole
variabili azione.
Dimostrazione omessa.
Definizione:
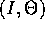si dicono
variabili azione-angolo per la hamiltoniana data e l'intorno
dato.
Il teorema di Arnold-Jost fornisce la soluzione espressa mediante le variabili azione-angolo. Poiché la trasformazione canonica che definisce le variabili azione-angolo è esprimibile mediante quadrature ed inversioni, (si veda [Arnold 86], Capitolo 10), i sistemi integrabili nel senso sopra definito sono integrabili mediante operazioni di quadratura ed esplicitazione di funzioni implicite.