



Next: B.3 TOPOLOGIAVARIETÀ
Up: B REQUISITI DI ALGEBRA
Previous: B.1 ALGEBRA LINEAREPOLINOMI
Una funzione è differenziabile se è approssimabile
nell'intorno di ogni punto con una funzione lineare, con resto di
ordine di infinitesimo superiore al primo nella distanza dal punto.
Il differenziale è l'applicazione lineare approssimante, che è
espressa (nelle basi canoniche degli spazi di partenza e di arrivo) da
una matrice detta matrice jacobiana. Una funzione  è sempre
differenziabile. La composta di due funzioni differenziabili è
differenziabile, e la sua matrice jacobiana, associata
all'applicazione lineare composta, è il prodotto righe per colonne
delle due matrici jacobiane (con la jacobiana della seconda funzione a
sinistra).
è sempre
differenziabile. La composta di due funzioni differenziabili è
differenziabile, e la sua matrice jacobiana, associata
all'applicazione lineare composta, è il prodotto righe per colonne
delle due matrici jacobiane (con la jacobiana della seconda funzione a
sinistra).
Teorema delle derivate miste : Se
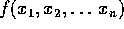 è una funzione definita e di classe
è una funzione definita e di classe
 (su di un aperto
(su di un aperto 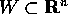 ), allora le derivate
seconde miste sono uguali:
), allora le derivate
seconde miste sono uguali:
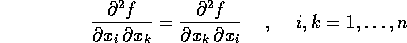
Quindi la matrice hessiana delle derivate seconde
è simmetrica.
Un punto di minimo locale forte è dove una funzione assume un
valore strettamente minore di tutti i valori assunti in un intorno; se
una funzione è di classe  , in un punto ha gradiente nullo e
matrice hessiana definita positiva, allora ha un punto di minimo
locale forte.
, in un punto ha gradiente nullo e
matrice hessiana definita positiva, allora ha un punto di minimo
locale forte.
Teorema delle funzioni implicite :
Sia 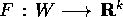 , di classe
, di classe 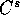 (con
(con 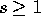 ) sull'aperto W di
) sull'aperto W di  , con n>k, e
, con n>k, e  un punto di W con
un punto di W con
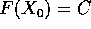 . Se la matrice jacobiana di F ha rango massimo k,
allora esiste una funzione
. Se la matrice jacobiana di F ha rango massimo k,
allora esiste una funzione 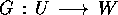 , con U
un intorno di
, con U
un intorno di 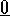 in
in 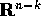 , di classe
, di classe 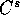 e tale che
e tale che
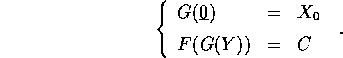
Questa funzione è localmente unica, cioè non ci sono in un intorno
di  altri punti soddisfacenti a F(X)=C salvo le immagini di
G; inoltre la matrice jacobiana
altri punti soddisfacenti a F(X)=C salvo le immagini di
G; inoltre la matrice jacobiana 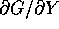 ha rango
massimo n-k.
ha rango
massimo n-k.
In effetti si può fare in modo che le coordinate Y che
parametrizzano l'insieme delle soluzioni di F(X)=C siano alcune
delle coordinate X, ossia si può fare in modo che l'equazione
F(X)=C definisca implicitamente delle funzioni che esprimono k
delle n coordinate in funzione delle altre n-k. Inoltre è anche
possibile ottenere una dipendenza differenziabile (sempre di classe
 ) di queste funzioni implicite dalle costanti C.
) di queste funzioni implicite dalle costanti C.
Un corollario del teorema delle funzioni implicite tratta il caso che
in un certo senso è opposto, quello delle funzioni
funzionalmente dipendenti . Se 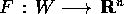 , di classe
, di classe 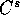 sull'aperto W di
sull'aperto W di 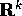 , ha matrice jacobiana
che non ha rango massimo, ma ha rango costante r< k su W, allora
si possono, almeno localmente (nell'intorno di ogni punto di W)
ricavare k-r componenti di F come funzioni delle altre r. Se al
contrario la matrice jacobiana ha rango massimo, le funzioni
componenti di F si dicono funzionalmente indipendenti . Un
altro corollario è il seguente:
, ha matrice jacobiana
che non ha rango massimo, ma ha rango costante r< k su W, allora
si possono, almeno localmente (nell'intorno di ogni punto di W)
ricavare k-r componenti di F come funzioni delle altre r. Se al
contrario la matrice jacobiana ha rango massimo, le funzioni
componenti di F si dicono funzionalmente indipendenti . Un
altro corollario è il seguente:
Teorema della funzione inversa :
Sia 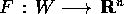 , di classe
, di classe 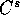 (con
(con 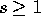 ) sull'aperto W di
) sull'aperto W di  , con n>k, e
, con n>k, e  un punto di W con
un punto di W con
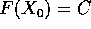 . Se la matrice jacobiana di F è invertibile (cioè se
lo jacobiano è
. Se la matrice jacobiana di F è invertibile (cioè se
lo jacobiano è 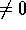 ), allora esiste una funzione
), allora esiste una funzione 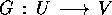 con U un intorno di C, e V un intorno di
con U un intorno di C, e V un intorno di
 , di classe
, di classe 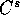 , che è l'inversa di F ristretta a V:
, che è l'inversa di F ristretta a V:
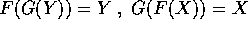 .
.
Le due applicazioni F,G si dicono diffeomorfismi locali.
In questo testo si utilizza la teoria della
integrazione di Riemann ,
nella quale gli integrali sono definiti usando il limite per
ampiezza della partizione che tende a zero. Un insieme sul quale
si può integrare la funzione 1, ottenendone l'area (nel piano; il
volume, nello spazio 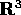 , eccetera), si dice
misurabile secondo Peano-Jordan .
, eccetera), si dice
misurabile secondo Peano-Jordan .
Teorema di integrabilità delle funzioni continue :
Una funzione continua su di un insieme misurabile secondo
Peano-Jordan ammette sempre l'integrale di Riemann.
Con procedimenti del tutto simili si può definire
l'integrale definito in una variabile,
l'integrale doppio di una qualsiasi funzione limitata
e continua su di un insieme misurabile, e anche
l'integrale triplo e l'integrale multiplo .
Nel seguito ci occuperemo di integrali doppi.
Teorema del cambiamento di variabili negli integrali doppi :
Dato un insieme misurabile (secondo Peano-Jordan) 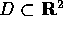 , ed
un diffeomorfismo
, ed
un diffeomorfismo
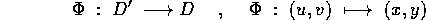
allora l'integrale doppio di una funzione continua f(x,y) su D si
può calcolare mediante un integrale nelle variabili (u,v):
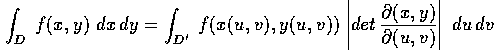
Per esempio, se la funzione da integrare è identicamente uguale ad
1, si trova che un diffeomorfismo conserva l'area se e solo se
il determinante jacobiano vale 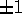 in ogni punto. Però se il
determinante è -1, il diffeomorfismo non
conserva l'orientazione , ossia manda angoli positivi
(antiorari) in angoli
negativi (orari). Perciò in molte applicazioni, come nel caso dei
sistemi conservativi, si richiede che l'area venga conservata ``con il
segno'', cioè con determinante jacobiano identicamente uguale ad 1.
in ogni punto. Però se il
determinante è -1, il diffeomorfismo non
conserva l'orientazione , ossia manda angoli positivi
(antiorari) in angoli
negativi (orari). Perciò in molte applicazioni, come nel caso dei
sistemi conservativi, si richiede che l'area venga conservata ``con il
segno'', cioè con determinante jacobiano identicamente uguale ad 1.
In modo del tutto analogo, sempre con il valore assoluto del
determinante jacobiano, si può operare anche un
cambiamento di variabile negli integrali multipli .
Una curva regolare è una parametrizzazione, cioè una
funzione 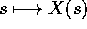 definita su di un intervallo di
definita su di un intervallo di 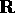 ed a
valori in
ed a
valori in  , che sia differenziabile (di classe almeno
, che sia differenziabile (di classe almeno  ) e
la cui velocità dX/ds(s) non si annulla per nessun s. Le
soluzioni di sistemi dinamici continui sono sempre curve regolari, con
il tempo come parametro, salvo che nel caso dei punti di equilibrio
(le uniche soluzioni per cui la velocità si annulla).
) e
la cui velocità dX/ds(s) non si annulla per nessun s. Le
soluzioni di sistemi dinamici continui sono sempre curve regolari, con
il tempo come parametro, salvo che nel caso dei punti di equilibrio
(le uniche soluzioni per cui la velocità si annulla).
Un integrale di linea di una forma differenziale lineare
nel piano (x,y) viene indicato come 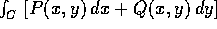 dove C è una curva regolare; se
dove C è una curva regolare; se 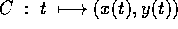 è la parametrizzazione della curva con due
funzioni
è la parametrizzazione della curva con due
funzioni  , con
, con 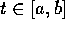 , allora l'integrale di linea è per
definizione uguale all'integrale definito:
, allora l'integrale di linea è per
definizione uguale all'integrale definito:
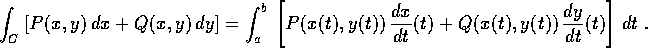
La forma differenziale lineare è l'espressione 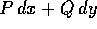 ; il
vettore dei suoi coefficienti è covariante . Poiché il
vettore velocità (dx/dt, dy/dt) è invece
controvariante , se si cambia sistema di coordinate
l'integrale di linea non cambia.
; il
vettore dei suoi coefficienti è covariante . Poiché il
vettore velocità (dx/dt, dy/dt) è invece
controvariante , se si cambia sistema di coordinate
l'integrale di linea non cambia.
Un insieme D del piano 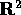 ha bordo
ha bordo  se C
è la frontiera di D, e al tempo stesso è l'immagine di
una curva regolare. Inoltre si richiede che la parametrizzazione sia
tale che la curva si lascia D a sinistra del vettore velocità.
Nella teoria dell'integrazione si può anche considerare una
curva regolare a tratti , per cui per esempio si può integrare
sul bordo di un poligono (con lati rettilinei, o curvilinei).
se C
è la frontiera di D, e al tempo stesso è l'immagine di
una curva regolare. Inoltre si richiede che la parametrizzazione sia
tale che la curva si lascia D a sinistra del vettore velocità.
Nella teoria dell'integrazione si può anche considerare una
curva regolare a tratti , per cui per esempio si può integrare
sul bordo di un poligono (con lati rettilinei, o curvilinei).
La formula di Green per l'area fornisce una relazione tra
l'integrale doppio che definisce l'area di un insieme piano D, ed un
integrale di linea sulla curva che ne forma il bordo 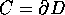 :
:
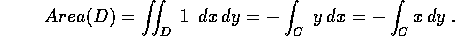
Una forma chiusa si ha quando le funzioni P(x,y) e Q(x,y) sono
 ed il rotore
ed il rotore

è identicamente nullo (su di un aperto  ). Una forma
differenziale lineare su di un aperto
). Una forma
differenziale lineare su di un aperto  è una
forma esatta quando
è una
forma esatta quando 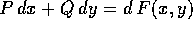 , ossia
quando le due funzioni
, ossia
quando le due funzioni 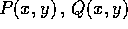 definiscono un
campo vettoriale conservativo che coincide con il gradiente di una
funzione differenziabile F:
definiscono un
campo vettoriale conservativo che coincide con il gradiente di una
funzione differenziabile F:
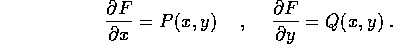
Una forma differenziale chiusa su di un aperto 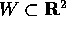 (cioè
un campo vettoriale con rotore identicamente nullo su tutto W) è
sempre localmente esatta, su di un intorno di ogni punto di W;
viceversa una forma localmente esatta (con coefficienti di classe
almeno
(cioè
un campo vettoriale con rotore identicamente nullo su tutto W) è
sempre localmente esatta, su di un intorno di ogni punto di W;
viceversa una forma localmente esatta (con coefficienti di classe
almeno  ) è anche chiusa, per il teorema delle
derivate miste . Poiché il gradiente di una funzione, e
la forma differenziale lineare corrispondente, si trasformano nello
stesso modo covariante , la proprietà di essere localmente
esatta (quindi chiusa) non dipende dal sistema di coordinate impiegato.
) è anche chiusa, per il teorema delle
derivate miste . Poiché il gradiente di una funzione, e
la forma differenziale lineare corrispondente, si trasformano nello
stesso modo covariante , la proprietà di essere localmente
esatta (quindi chiusa) non dipende dal sistema di coordinate impiegato.
Non è invece detto che una forma chiusa sia esatta; in generale
sarà la forma 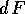 associata ad una
funzione polidroma F.
Se però l'insieme W soddisfa ad opportune condizioni
topologiche, come quella di essere ``semplicemente connesso'' allora
ogni forma chiusa sarà esatta.
associata ad una
funzione polidroma F.
Se però l'insieme W soddisfa ad opportune condizioni
topologiche, come quella di essere ``semplicemente connesso'' allora
ogni forma chiusa sarà esatta.
La teoria degli integrali di linea, e delle
forme differenziali lineari ,
si estende facilmente ad  con n>2: se
con n>2: se 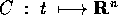 è una curva
è una curva  sull'intervallo [a,b],
sull'intervallo [a,b],
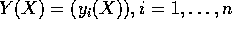
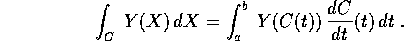
Al campo vettoriale gradiente di una funzione è associata una forma
differenziale, con le componenti del gradiente come coefficienti:
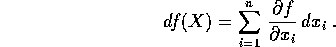
Una forma differenziale lineare 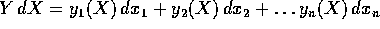 è una
forma esatta se
esiste una funzione f(X) tale che
è una
forma esatta se
esiste una funzione f(X) tale che 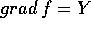 , ossia tale che
, ossia tale che
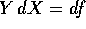 . Le forme differenziali lineari si trasformano, al cambiare
delle coordinate, come i gradienti, cioè i coefficienti cambiano in
modo covariante ; la condizione di esattezza non dipende dal
sistema di coordinate usato.
Una condizione necessaria e sufficiente
perché una forma (con coefficienti
. Le forme differenziali lineari si trasformano, al cambiare
delle coordinate, come i gradienti, cioè i coefficienti cambiano in
modo covariante ; la condizione di esattezza non dipende dal
sistema di coordinate usato.
Una condizione necessaria e sufficiente
perché una forma (con coefficienti  ) sia localmente esatta è
che valgano le condizioni imposte dal teorema delle derivate
miste; condizioni che corrispondono all'annullamento
dell'analogo multidimensionale del rotore.
) sia localmente esatta è
che valgano le condizioni imposte dal teorema delle derivate
miste; condizioni che corrispondono all'annullamento
dell'analogo multidimensionale del rotore.
Per calcolare queste condizioni in  , con n>2,
conviene definire una forma differenziale quadratica ,
che è un'espressione della forma
, con n>2,
conviene definire una forma differenziale quadratica ,
che è un'espressione della forma
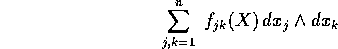
nelle quali si possono raccogliere i termini sulla base della regola
di antisimmetria: 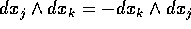 . Quindi ad ogni
forma differenziale quadratica è associata in modo unico una matrice
antisimmetrica dei suoi coefficienti:
. Quindi ad ogni
forma differenziale quadratica è associata in modo unico una matrice
antisimmetrica dei suoi coefficienti:
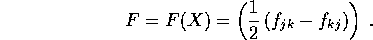
Una forma differenziale quadratica si trasforma, per effetto di un
cambiamento di coordinate con matrice jacobiana A, in modo tale che
la matrice antisimmetrica F dei suoi coefficienti viene
moltiplicata a sinistra per A ed a destra per 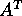 :
:
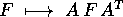 .
.
Si definisce inoltre l'operatore di differenziazione esterna ,
che manda forme differenziali lineari in forme differenziali
quadratiche:
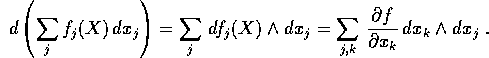
La proprietà fondamentale dell'operatore di differenziazione esterna
è appunto di annullarsi su di una forma differenziale lineare esatta:
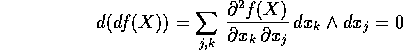
a condizione che la funzione f(X) sia di classe  , in modo da
poter applicare il teorema delle derivate miste .
, in modo da
poter applicare il teorema delle derivate miste . 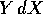 si dice una forma chiusa se il suo
differenziale esterno è la forma differenziale quadratica a
coefficienti tutti nulli:
si dice una forma chiusa se il suo
differenziale esterno è la forma differenziale quadratica a
coefficienti tutti nulli: 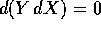 ; anche questa condizione non
dipende dal sistema di coordinate usato. La condizione di chiusura è
quindi necessaria perché una forma differenziale lineare (a
coefficienti
; anche questa condizione non
dipende dal sistema di coordinate usato. La condizione di chiusura è
quindi necessaria perché una forma differenziale lineare (a
coefficienti  ) sia esatta; questa condizione non è sempre
sufficiente, ma vale il seguente risultato:
) sia esatta; questa condizione non è sempre
sufficiente, ma vale il seguente risultato:
Teorema di Poincaré : Ogni forma differenziale
lineare, di classe  , che sia chiusa, è anche esatta localmente,
cioè in un opportuno intorno di ogni punto.
, che sia chiusa, è anche esatta localmente,
cioè in un opportuno intorno di ogni punto.
La struttura simplettica dello spazio delle fasi di coordinate
(P,Q) è definita dai coefficienti della matrice J, che sono poi (a
meno di un segno) quelli della forma differenziale quadratica
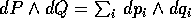 . Nel caso ad un grado di
libertà la forma
. Nel caso ad un grado di
libertà la forma 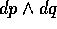 è l'elemento d'area, e questo
consente di identificare le trasformazioni canoniche con quelle che
conservano l'area. Per questo tipo di formalismo, si veda
[Arnold 86], capitoli 7 ed 8.
è l'elemento d'area, e questo
consente di identificare le trasformazioni canoniche con quelle che
conservano l'area. Per questo tipo di formalismo, si veda
[Arnold 86], capitoli 7 ed 8.
Una generalizzazione notevole della teoria dell'integrazione si
ottiene definendo gli integrali su sottovarietà di  . Per
esempio, per n=3, su di una superficie regolare S dotata in ogni
punto di un versore normale N, è possibile definire il flusso di
un campo vettoriale
. Per
esempio, per n=3, su di una superficie regolare S dotata in ogni
punto di un versore normale N, è possibile definire il flusso di
un campo vettoriale 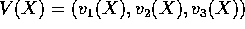 , dando senso al simbolo
, dando senso al simbolo

in modo che valga la formula di Gauss : se
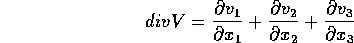
e W è un solido in 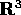 di cui S è il bordo (frontiera
che è anche superficie regolare), allora
di cui S è il bordo (frontiera
che è anche superficie regolare), allora
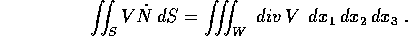
Un campo vettoriale V che sia solenoidale ha quindi la
proprietà che il suo flusso attraverso ogni superficie che fa da
bordo è nullo. Questa proprietà si applica per esempio al campo
gravitazionale al di fuori dei corpi che lo generano.
Un altro tipo di integrale di linea è quello che si usa per definire
la lunghezza della curva : se 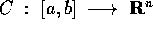 è una parametrizzazione
è una parametrizzazione  per la curva X=C(t), allora la
lunghezza può essere definita come
per la curva X=C(t), allora la
lunghezza può essere definita come
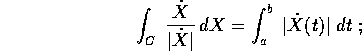
una parametrizzazione della stessa curva X=B(s) tale che 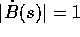 ha quindi la proprietà di avere parametro arco ,
cioè la lunghezza di un arco di curva coincide (a meno del segno)
con l'incremento del parametro s.
ha quindi la proprietà di avere parametro arco ,
cioè la lunghezza di un arco di curva coincide (a meno del segno)
con l'incremento del parametro s.
Bibliografia :
- Prodi, G. : Lezioni di Analisi Matematica, Parte II,
Editrice Tecnico Scientifica, Pisa, 1974.
- Stampacchia, G. : Lezioni di analisi matematica, volume
secondo, Liguori Editore, Napoli, 1973.




Next: B.3 TOPOLOGIAVARIETÀ
Up: B REQUISITI DI ALGEBRA
Previous: B.1 ALGEBRA LINEAREPOLINOMI
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
 è sempre
differenziabile. La composta di due funzioni differenziabili è
differenziabile, e la sua matrice jacobiana, associata
all'applicazione lineare composta, è il prodotto righe per colonne
delle due matrici jacobiane (con la jacobiana della seconda funzione a
sinistra).
è sempre
differenziabile. La composta di due funzioni differenziabili è
differenziabile, e la sua matrice jacobiana, associata
all'applicazione lineare composta, è il prodotto righe per colonne
delle due matrici jacobiane (con la jacobiana della seconda funzione a
sinistra).
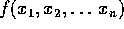 è una funzione definita e di classe
è una funzione definita e di classe
 (su di un aperto
(su di un aperto 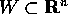 ), allora le derivate
seconde miste sono uguali:
), allora le derivate
seconde miste sono uguali:
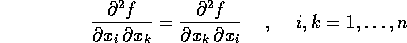
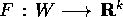 , di classe
, di classe 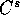 (con
(con 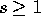 ) sull'aperto W di
) sull'aperto W di  , con n>k, e
, con n>k, e  un punto di W con
un punto di W con
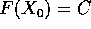 . Se la matrice jacobiana di F ha rango massimo k,
allora esiste una funzione
. Se la matrice jacobiana di F ha rango massimo k,
allora esiste una funzione 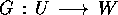 , con U
un intorno di
, con U
un intorno di 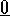 in
in 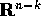 , di classe
, di classe 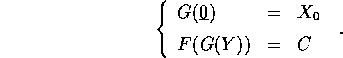
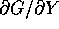 ha rango
massimo n-k.
ha rango
massimo n-k.
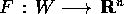 , di classe
, di classe 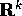 , ha matrice jacobiana
che non ha rango massimo, ma ha rango costante r< k su W, allora
si possono, almeno localmente (nell'intorno di ogni punto di W)
ricavare k-r componenti di F come funzioni delle altre r. Se al
contrario la matrice jacobiana ha rango massimo, le funzioni
componenti di F si dicono
, ha matrice jacobiana
che non ha rango massimo, ma ha rango costante r< k su W, allora
si possono, almeno localmente (nell'intorno di ogni punto di W)
ricavare k-r componenti di F come funzioni delle altre r. Se al
contrario la matrice jacobiana ha rango massimo, le funzioni
componenti di F si dicono 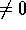 ), allora esiste una funzione
), allora esiste una funzione 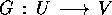 con U un intorno di C, e V un intorno di
con U un intorno di C, e V un intorno di
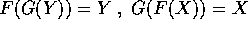 .
.
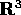 , eccetera), si dice
misurabile secondo Peano-Jordan
, eccetera), si dice
misurabile secondo Peano-Jordan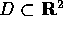 , ed
un diffeomorfismo
, ed
un diffeomorfismo
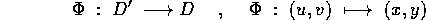
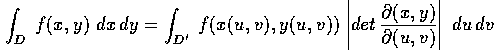
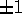 in ogni punto. Però se il
determinante è -1, il diffeomorfismo non
conserva l'orientazione
in ogni punto. Però se il
determinante è -1, il diffeomorfismo non
conserva l'orientazione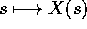 definita su di un intervallo di
definita su di un intervallo di 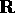 ed a
valori in
ed a
valori in 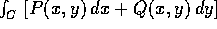 dove C è una curva regolare; se
dove C è una curva regolare; se 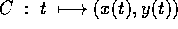 è la parametrizzazione della curva con due
funzioni
è la parametrizzazione della curva con due
funzioni 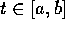 , allora l'integrale di linea è per
definizione uguale all'integrale definito:
, allora l'integrale di linea è per
definizione uguale all'integrale definito:
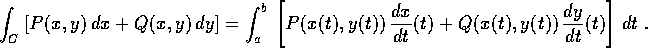
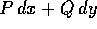 ; il
vettore dei suoi coefficienti è
; il
vettore dei suoi coefficienti è 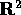 ha bordo
ha bordo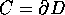 se C
è la
se C
è la 

 ). Una forma
differenziale lineare su di un aperto
). Una forma
differenziale lineare su di un aperto 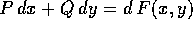 , ossia
quando le due funzioni
, ossia
quando le due funzioni 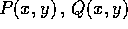 definiscono un
campo vettoriale conservativo
definiscono un
campo vettoriale conservativo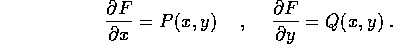
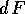 associata ad una
associata ad una
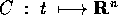 è una curva
è una curva 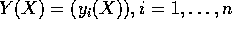
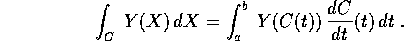
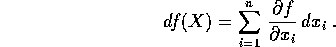
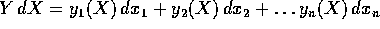 è una
forma esatta
è una
forma esatta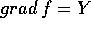 , ossia tale che
, ossia tale che
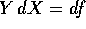 . Le forme differenziali lineari si trasformano, al cambiare
delle coordinate, come i gradienti, cioè i coefficienti cambiano in
modo
. Le forme differenziali lineari si trasformano, al cambiare
delle coordinate, come i gradienti, cioè i coefficienti cambiano in
modo 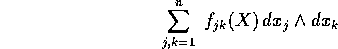
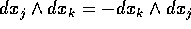 . Quindi ad ogni
forma differenziale quadratica è associata in modo unico una matrice
antisimmetrica dei suoi coefficienti:
. Quindi ad ogni
forma differenziale quadratica è associata in modo unico una matrice
antisimmetrica dei suoi coefficienti:
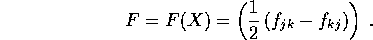
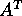 :
:
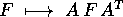 .
.
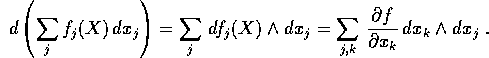
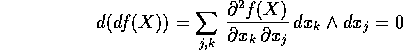
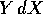 si dice una forma chiusa
si dice una forma chiusa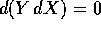 ; anche questa condizione non
dipende dal sistema di coordinate usato. La condizione di chiusura è
quindi necessaria perché una forma differenziale lineare (a
coefficienti
; anche questa condizione non
dipende dal sistema di coordinate usato. La condizione di chiusura è
quindi necessaria perché una forma differenziale lineare (a
coefficienti 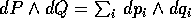 . Nel caso ad un grado di
libertà la forma
. Nel caso ad un grado di
libertà la forma 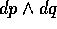 è l'elemento d'area, e questo
consente di identificare le trasformazioni canoniche con quelle che
conservano l'area. Per questo tipo di formalismo, si veda
[
è l'elemento d'area, e questo
consente di identificare le trasformazioni canoniche con quelle che
conservano l'area. Per questo tipo di formalismo, si veda
[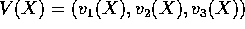 , dando senso al simbolo
, dando senso al simbolo

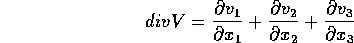
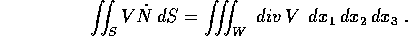
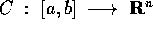 è una parametrizzazione
è una parametrizzazione 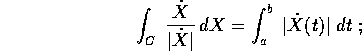
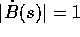 ha quindi la proprietà di avere parametro arco
ha quindi la proprietà di avere parametro arco