



Next: 1.4 NOTAZIONI E INDICI
Up: 1 DEFINIZIONI E PRIMI
Previous: 1.2 SISTEMI LINEARIINTEGRABILITÀ
Sommario Alcuni sistemi dinamici continui hanno degli invarianti,
cioè funzioni che si conservano ``lungo'' le soluzioni, al variare del
tempo nel flusso integrale. Una funzione che si conserva al passare
del tempo è un integrale primo. Altri invarianti sono esprimibili
mediante integrali, per esempio l'area. Definizioni analoghe si
applicano anche al caso discreto.
Esempio:
-
- Consideriamo un oscillatore armonico , cioè l'equazione
differenziale di ordine 2, cioè contenente una derivata
seconda:

che si può tradurre in un sistema
dinamico in 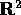 introducendo una seconda variabile y con
introducendo una seconda variabile y con
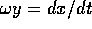 :
:
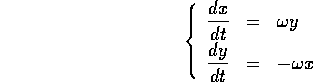
Le soluzioni sono tutte della forma
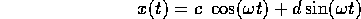
con c,d costanti
arbitrarie, che corrispondono alla condizione iniziale :
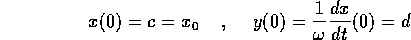
per cui vale anche:
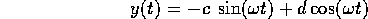
cioè in forma matriciale:
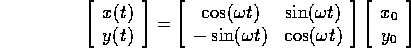
dove la matrice esprime una rotazione di un angolo 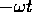 ,
cioè in verso orario se
,
cioè in verso orario se 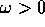 .
.
Questo esempio ha due proprietà speciali:
Definizione:
Ogni insieme di livello di E è un insieme
invariante .
Esempio:
-
- Nel caso dell'oscillatore armonico, esiste un integrale primo:
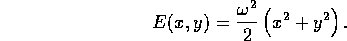
Calcolando la
derivata totale, cioè la derivata di E lungo una soluzione
(x(t), y(t)) con la formula usuale di derivazione delle funzioni
composte:
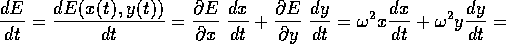
a questo punto sostituendo i secondi membri delle equazioni differenziali:

per cui il valore di E resta costante lungo ogni soluzione.
Definizione:
-
- Un sistema dinamico continuo su
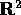 si dice
conservativo
se il suo flusso
integrale per ogni t fisso è una trasformazione di
si dice
conservativo
se il suo flusso
integrale per ogni t fisso è una trasformazione di 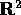 in
sé che conserva l'area (in valore ed in segno, cioè conserva
l'orientazione).
in
sé che conserva l'area (in valore ed in segno, cioè conserva
l'orientazione).
Esempio:
-
- Un oscillatore armonico, poiché il flusso integrale è
espresso da una rotazione della condizione iniziale (di un angolo
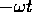 ), è conservativo.
), è conservativo.
Le condizioni per cui questo si verifica sono discusse nel
Capitolo 5. La generalizzazione al caso di dimensione
>2 viene discussa nel Capitolo 6.
Le definizioni date in questa sezione si possono adattare al
caso discreto, senza difficoltà. Occorre però fare attenzione a
che le definizioni date nel caso continuo, quando si procede ad una
discretizzazione 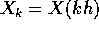 , si traducano nelle definizioni del
caso discreto.
, si traducano nelle definizioni del
caso discreto.
Definizione:
Esempio:
Definizione:
-
- Si ha un sistema dinamico discreto conservativo su
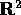 se la mappa che definisce il sistema dinamico conserva l'area (in
valore ed in segno, cioè conserva l'orientazione).
se la mappa che definisce il sistema dinamico conserva l'area (in
valore ed in segno, cioè conserva l'orientazione).
Esempio:
-
- Un sistema dinamico discreto lineare è della forma:

dove A è una matrice quadrata. Consideriamo il
caso in 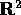 , cioè con la matrice A di tipo
, cioè con la matrice A di tipo 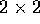 ; i
vettori della base canonica
; i
vettori della base canonica
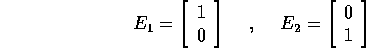
vengono trasformati
in 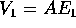 ,
, 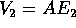 che coincidono con le colonne di A.
L'area del parallelogramma di lati
che coincidono con le colonne di A.
L'area del parallelogramma di lati 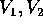 si calcola mediante il
modulo del prodotto vettore:
si calcola mediante il
modulo del prodotto vettore:
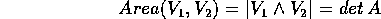
Perciò se 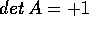 il sistema è conservativo.
il sistema è conservativo.
Si noti che ci sono due casi possibili, qualitativamente molto
diversi tra loro: nel primo A è una matrice di rotazione, che
quindi ha automaticamente determinante 1, nel secondo:





Next: 1.4 NOTAZIONI E INDICI
Up: 1 DEFINIZIONI E PRIMI
Previous: 1.2 SISTEMI LINEARIINTEGRABILITÀ
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997

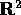 introducendo una seconda variabile y con
introducendo una seconda variabile y con
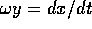 :
:
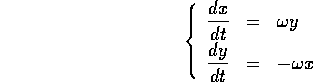
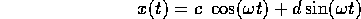
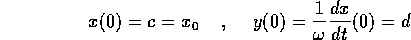
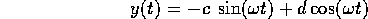
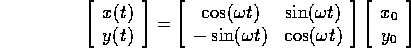
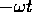 ,
cioè in verso orario se
,
cioè in verso orario se 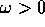 .
.
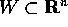 se E è una
funzione differenziabile su W tale che:
se E è una
funzione differenziabile su W tale che:
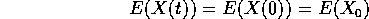
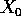 .
.
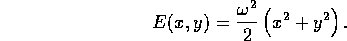
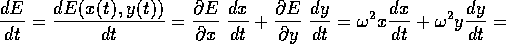

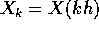 , si traducano nelle definizioni del
caso discreto.
, si traducano nelle definizioni del
caso discreto.
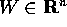 se E è una funzione
differenziabile su W tale che:
se E è una funzione
differenziabile su W tale che:

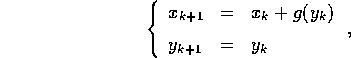

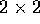 ; i
vettori della base canonica
; i
vettori della base canonica
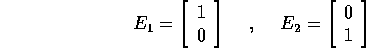
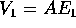 ,
, 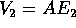 che coincidono con le colonne di A.
L'area del parallelogramma di lati
che coincidono con le colonne di A.
L'area del parallelogramma di lati 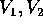 si calcola mediante il
modulo del prodotto vettore:
si calcola mediante il
modulo del prodotto vettore:
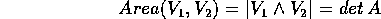
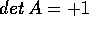 il sistema è conservativo.
il sistema è conservativo.
