 . Le soluzioni di questo
sistema dinamico sono esprimibili mediante l'esponenziale di
matrice, quindi la funzione soluzione dell'equazione differenziale
conterrà esponenziali, seni e coseni, polinomi.
. Le soluzioni di questo
sistema dinamico sono esprimibili mediante l'esponenziale di
matrice, quindi la funzione soluzione dell'equazione differenziale
conterrà esponenziali, seni e coseni, polinomi.
Sommario Un'equazione differenziale contenente le derivate fino
all'ordine n, indipendente dal tempo, e risolta rispetto alla
derivata di ordine più alto, si può ricondurre ad un
sistema dinamico continuo in  . Le soluzioni di questo
sistema dinamico sono esprimibili mediante l'esponenziale di
matrice, quindi la funzione soluzione dell'equazione differenziale
conterrà esponenziali, seni e coseni, polinomi.
. Le soluzioni di questo
sistema dinamico sono esprimibili mediante l'esponenziale di
matrice, quindi la funzione soluzione dell'equazione differenziale
conterrà esponenziali, seni e coseni, polinomi.
Definizione:
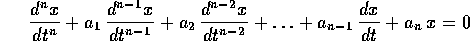
dove x(t) è una funzione
incognita, si chiama equazione differenziale lineare ; se
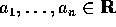 sono indipendenti da t si dice che
l'equazione è a coefficienti costanti . L'ordine
dell'equazione è il massimo ordine di derivazione n.
sono indipendenti da t si dice che
l'equazione è a coefficienti costanti . L'ordine
dell'equazione è il massimo ordine di derivazione n.
Si dice che l'equazione differenziale lineare è omogenea quando il secondo membro è identicamente zero, come qui sopra; l'equazione sarebbe invece non omogenea se il secondo membro fosse una funzione non nulla di t.
Ogni equazione differenziale lineare, omogenea e a coefficienti
costanti si può ridurre ad un
sistema dinamico continuo lineare .
A questo scopo se l'ordine è n basta definire
il vettore 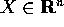 :
:
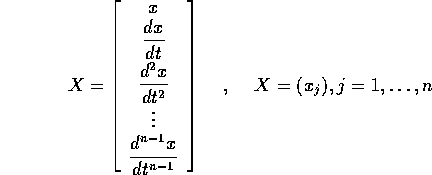
Ad ogni funzione x(t) di classe almeno 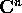 corrisponderà
una curva continua X(t) in
corrisponderà
una curva continua X(t) in  , che è soluzione del sistema
dinamico:
, che è soluzione del sistema
dinamico:
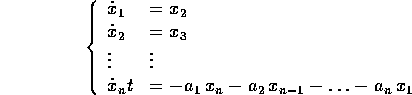
In forma matriciale:
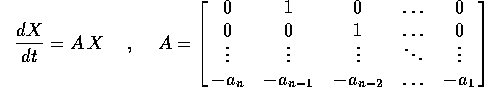
Le condizioni iniziali da assegnare per l'equazione di ordine n altro non sono che la condizione iniziale (vettoriale) del sistema dinamico corrispondente, cioè:
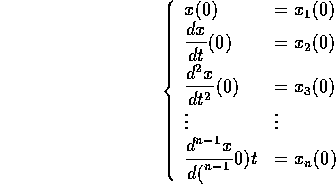
Se indichiamo queste condizioni iniziali con il vettore  , allora
la soluzione del sistema dinamico è
, allora
la soluzione del sistema dinamico è 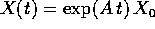 , e la
soluzione dell'equazione di ordine n è
, e la
soluzione dell'equazione di ordine n è 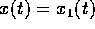 , quindi solo
la prima riga dell'esponenziale di matrice viene effettivamente usata
per esprimere la soluzione x(t).
, quindi solo
la prima riga dell'esponenziale di matrice viene effettivamente usata
per esprimere la soluzione x(t).
Definizione:
 , soluzione di un'equazione differenziale lineare , di
ordine 2, omogenea ed a
coefficienti costanti :
, soluzione di un'equazione differenziale lineare , di
ordine 2, omogenea ed a
coefficienti costanti :
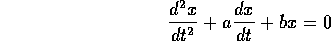
con 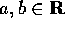 .
.
Costruiamo il corrispondente sistema dinamico in 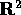 , ponendo dx/dt=y:
, ponendo dx/dt=y:
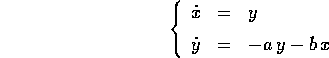
In forma matriciale:
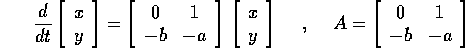
L'equazione caratteristica della matrice A è:
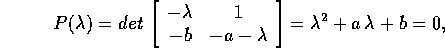
e la forma analitica del flusso integrale, in funzione delle
condizioni iniziali 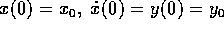 , dipende
solo dal segno del discriminante
, dipende
solo dal segno del discriminante

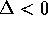 , gli autovalori sono complessi:
, gli autovalori sono complessi:
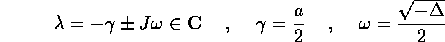
perciò le soluzioni sono esprimibili come combinazioni lineari
della funzione esponenziale 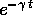 moltiplicata per
moltiplicata per
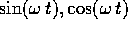 :
:
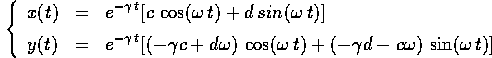
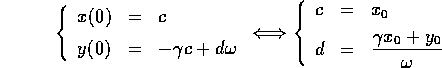
Questo calcolo si può eseguire con il metodo delle ampiezze complesse , che si usa per risolvere anche il caso non omogeneo (vedi Sezione 8.2).
Procedimento alternativo: un autovettore complesso di autovalore
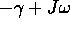 è:
è:
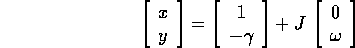
allora si usa il procedimento si riduzione in forma canonica visto nel caso di due autovalori coniugati , cioè si usa come base la parte reale e la parte immaginaria dell'autovettore:
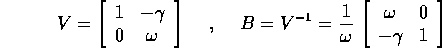
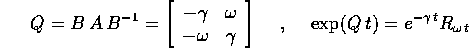
da cui la soluzione del sistema dinamico, con le formule abituali:
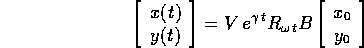
e la soluzione dell'equazione del secondo ordine:
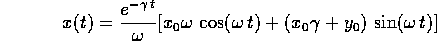
Negli esempi più importanti di applicazioni, 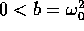 e
e
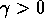 ma piccolo rispetto a
ma piccolo rispetto a 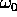 , per cui
, per cui

e la soluzione è un'oscillazione smorzata che tende a zero per
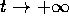 (Figura 2.6).
(Figura 2.6).
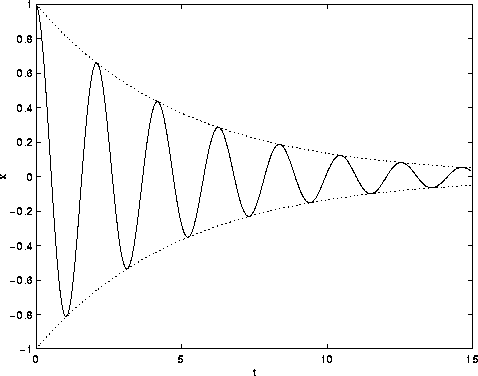
Figure 2.6: Oscillazione smorzata: la funzione
exp(-t/5) cos(3t).
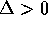 , gli autovalori sono reali:
, gli autovalori sono reali:
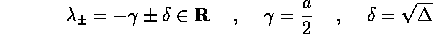
e le soluzioni sono esprimibili come combinazioni lineari delle
due esponenziali di esponenti 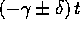 :
:
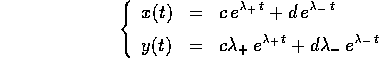
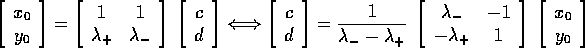
Procedimento alternativo: degli autovettori reali di autovalori
rispettivamente 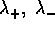 sono:
sono:
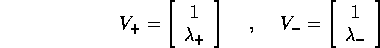
ed il cambiamento di coordinate lineare che passa alla
nuova base 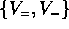 è espresso dalle matrici:
è espresso dalle matrici:
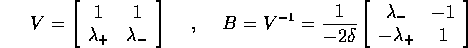
con il flusso integrale:
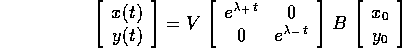
e la soluzione dell'equazione di ordine 2:
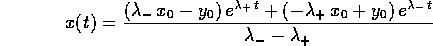
Il comportamento qualitativo delle soluzioni
per 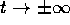 dipende dal segno di
dipende dal segno di 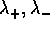 ,
e quindi di a,b; per esempio se a,b>0, allora
,
e quindi di a,b; per esempio se a,b>0, allora 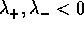 ed il limite per
ed il limite per 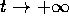 è zero.
è zero.
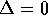 , un autovalore reale di
molteplicità algebrica 2:
, un autovalore reale di
molteplicità algebrica 2:

perciò le soluzioni sono esprimibili come combinazioni lineari di
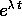 e di
e di 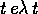 :
:

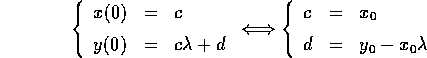
Procedimento alternativo: tutti gli autovettori di autovalore
 sono multipli di:
sono multipli di:

e come nel procedimento di riduzione in
forma canonica del nilpotente si sceglie
un  arbitrario, purché non sia un
autovettore (cioè indipendente da
arbitrario, purché non sia un
autovettore (cioè indipendente da  ):
):
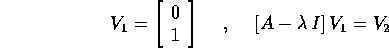
e quindi nella base 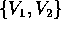 la matrice A diventa:
la matrice A diventa:
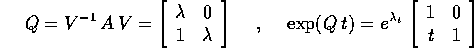
il flusso integrale è:
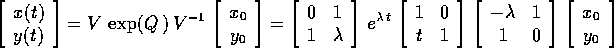
e la soluzione dell'equazione di ordine 2:
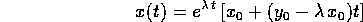
Esercizio
Una molla di costante elastica k>0, lunghezza a riposo 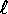 e
massa trascurabile è vincolata lungo una guida orizzontale, sulla
quale è fissata ad un estremo; all'altro è fissato un punto P di
massa m. Supponendo che la guida si opponga al moto di P con una
resistenza proporzionale alla velocità con coefficiente
e
massa trascurabile è vincolata lungo una guida orizzontale, sulla
quale è fissata ad un estremo; all'altro è fissato un punto P di
massa m. Supponendo che la guida si opponga al moto di P con una
resistenza proporzionale alla velocità con coefficiente 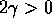 ,
determinare di quanto si deve spostare P dalla posizione di riposo
della molla affinché, rilasciandolo, dopo T unità di tempo
l'ampiezza delle sue oscillazioni smorzate sia ancora superiore a
L/3.
(Soluzione)
,
determinare di quanto si deve spostare P dalla posizione di riposo
della molla affinché, rilasciandolo, dopo T unità di tempo
l'ampiezza delle sue oscillazioni smorzate sia ancora superiore a
L/3.
(Soluzione)
Esercizio
Se nell'esercizio precedente, invece di assegnare le condizioni
iniziali su x e 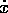 , si richiede che siano verificate le
condizioni ai limiti in due istanti fissati, 0 e T,
, si richiede che siano verificate le
condizioni ai limiti in due istanti fissati, 0 e T,
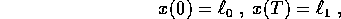
il problema ha sempre soluzione ? (Soluzione)
Esempio:
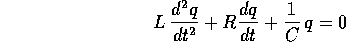
dove L>0 è l'induttanza , R>0 la resistenza , C>0 la capacità .
Basta dividere per L per riconoscere che questa equazione è quella dell'oscillatore lineare , con la sola particolarità di avere coefficienti tutti >0. Il discriminante è:

Per valori abbastanza grandi della resistenza gli autovalori sono reali ed ogni soluzione è una combinazione di esponenziali con esponenti negativi. Per valori abbastanza piccoli della resistenza ogni soluzione è un'oscillazione smorzata . Di questo si può dare un'interpretazione in termini di energia dissipata dalla resistenza.
Introduciamo la notazione degli operatori differenziali :
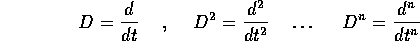
in modo che ad ogni polinomio 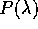 di grado n:
di grado n:
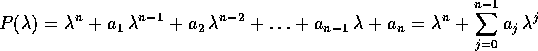
corrisponda una combinazione di derivate, come quella che appare nelle equazioni differenziali lineari di ordine n:
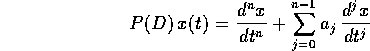
Definizione:
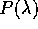 come sopra, si dice matrice compagna
la matrice
come sopra, si dice matrice compagna
la matrice  :
:
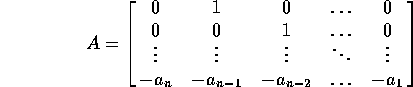
Se si trasforma l'equazione differenziale lineare a
coefficienti costanti 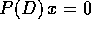 in un sistema dinamico
lineare in
in un sistema dinamico
lineare in  , la matrice del sistema dinamico è proprio la
matrice compagna del polinomio con gli stessi coefficienti
dell'equazione differenziale.
, la matrice del sistema dinamico è proprio la
matrice compagna del polinomio con gli stessi coefficienti
dell'equazione differenziale.
Teorema dell' operatore differenziale lineare :
Il polinomio P ha la radice  se e solo se la funzione esponenziale
se e solo se la funzione esponenziale
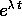 è una soluzione dell'equazione differenziale
lineare omogenea con gli stessi coefficienti:
è una soluzione dell'equazione differenziale
lineare omogenea con gli stessi coefficienti:

Se la radice 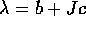 è complessa, allora le soluzioni
corrispondenti sono
è complessa, allora le soluzioni
corrispondenti sono 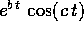 e
e 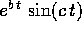 .
.
Dimostrazione:
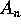 è la matrice compagna del polinomio
è la matrice compagna del polinomio 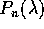 di grado n, allora la sua equazione caratteristica è:
di grado n, allora la sua equazione caratteristica è:
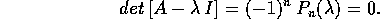
Dimostrazione del lemma:
Infatti se usiamo lo sviluppo di Laplace rispetto alla prima colonna
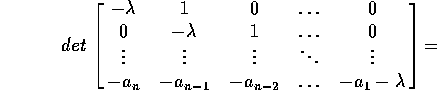
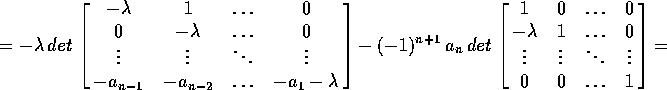
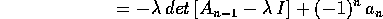
dove 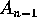 è la matrice compagna del polinomio
è la matrice compagna del polinomio
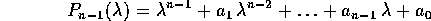
Nel caso dell'oscillatore lineare abbiamo visto che
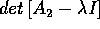 è
è 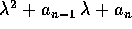 , e
questo completa la dimostrazione per induzione.
, e
questo completa la dimostrazione per induzione.
Il teorema segue dal lemma e dall'applicazione del teorema delle soluzioni del sistema dinamico lineare .
Problema Una dimostrazione alternativa del teorema qui sopra usa le formule:
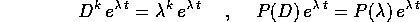
Verificare che
queste formule valgono sia per 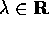 che per
che per 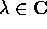 .
.
Esercizio Risolvere l'equazione omogenea del quarto ordine
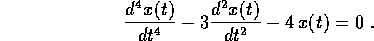
Per soddisfare alle n condizioni iniziali , di un'equazione differenziale di ordine n, occorre uno spazio vettoriale di soluzioni di dimensione n. Quindi se gli autovalori della matrice compagna sono tutti distinti (reali o complessi a coppie coniugate) ci sono abbastanza soluzioni linearmente indipendenti fornite dal teorema dell'operatore differenziale lineare . Se ci sono autovalori multipli, il nilpotente di ciascun blocco di Jordan introduce dei polinomi nell'esponenziale di matrice, e quindi anche nella soluzione dell'equazione di ordine n.
Teorema delle soluzioni dell'equazione a coefficienti costanti : Per ogni insieme di condizioni iniziali esiste una soluzione dell'equazione differenziale lineare di ordine n:

che è una combinazione lineare delle n funzioni seguenti:
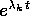 per ogni radice reale
per ogni radice reale 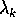 di P(z)=0.
di P(z)=0.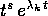 con
con 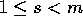 per ogni radice reale
per ogni radice reale
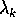 di molteplicità m.
di molteplicità m.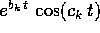 ed
ed 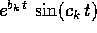 per ogni coppia
per ogni coppia 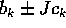 di radici complesse coniugate di
P(z)=0.
di radici complesse coniugate di
P(z)=0.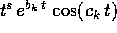 e
e
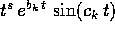 con
con 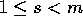 per ogni coppia
per ogni coppia
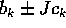 di radici complesse coniugate di molteplicità m.
di radici complesse coniugate di molteplicità m.
Utilizzando il teorema di esistenza e unicità si dimostra che non ci sono altre soluzioni dell'equazione differenziale lineare data, e quindi le soluzioni elencate sopra formano una base dello spazio vettoriale delle soluzioni; vedi Sezione 8.4.
Dimostrazione:
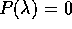 coincide con l'equazione
caratteristica della matrice compagna, si utilizza il teorema
delle soluzioni del sistema dinamico lineare . Il solo
problema è provare che la matrice nilpotente associata a
ciascun autovalore ha ordine del nilpotente massimo.
coincide con l'equazione
caratteristica della matrice compagna, si utilizza il teorema
delle soluzioni del sistema dinamico lineare . Il solo
problema è provare che la matrice nilpotente associata a
ciascun autovalore ha ordine del nilpotente massimo.
Lemma:
Dimostrazione del lemma:
Per il teorema di Jordan il numero dei blocchi
e la molteplicità dell'autovalore , cioè il numero di autovettori
linearmente indipendenti, coincidono. Ma la dimensione dell'autospazio
è la dimensione del nucleo di 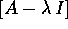 : nel caso della
matrice compagna contiene sempre il minore ottenuto togliendo la
prima colonna e l'ultima riga, che ha tutti coefficienti 1 sulla
diagonale principale, e quindi ha sempre rango almeno n-1,
qualunque sia
: nel caso della
matrice compagna contiene sempre il minore ottenuto togliendo la
prima colonna e l'ultima riga, che ha tutti coefficienti 1 sulla
diagonale principale, e quindi ha sempre rango almeno n-1,
qualunque sia  . Quindi ogni autospazio ha dimensione 1, ed
il blocco di Jordan opera su di uno spazio di dimensione pari alla
molteplicità algebrica.
. Quindi ogni autospazio ha dimensione 1, ed
il blocco di Jordan opera su di uno spazio di dimensione pari alla
molteplicità algebrica.
La dimostrazione si conclude esprimendo la soluzione dell'equazione differenziale lineare di ordine n, con condizioni iniziali date, mediante il flusso integrale del sistema dinamico lineare.
Resterebbe da verificare che tutte le funzioni elencate
nel'enunciato appaiono non solo nell'esponenziale 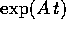 della
matrice compagna A, ma anche nella soluzione x(t), cioè nella
prima riga di
della
matrice compagna A, ma anche nella soluzione x(t), cioè nella
prima riga di 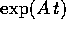 . Segue dalla proprietà dei
quasipolinomi che il grado del polinomio non diminuisce
derivando.
. Segue dalla proprietà dei
quasipolinomi che il grado del polinomio non diminuisce
derivando.
Problema
L'operatore 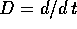 di derivazione è un operatore lineare sullo
spazio delle funzioni derivabili.
In particolare, se
di derivazione è un operatore lineare sullo
spazio delle funzioni derivabili.
In particolare, se 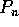 è lo spazio di dimensione finita dei
polinomi di grado N a coefficienti
reali (o complessi),
è lo spazio di dimensione finita dei
polinomi di grado N a coefficienti
reali (o complessi),
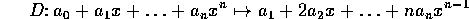
può essere rappresentato da una matrice. Determinarne la forma canonica e la relativa base. (Soluzione)
Un metodo alternativo per risolvere un'equazione differenziale lineare omogenea è quello di considerare lo spazio dei quasipolinomi , seguendo lo stesso procedimento usato per risolvere il caso di un equazione non omogenea ; si veda la Sezione 8.2.)