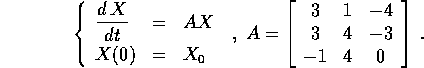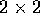Sommario Se la matrice di un sistema dinamico lineare ha autovalori
complessi, non è diagonalizzabile. Però può essere
diagonalizzabile in campo complesso. Ad ogni coppia di autovalori
complessi coniugati corrisponde un blocco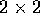 
che si può
mettere in una forma canonica. Queste forme canoniche costituiscono un
modello del campo complesso.
Tra le matrici a coefficienti reali di tipo 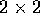consideriamo il
sottospazio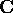 
di dimensione 2 delle matrici della forma
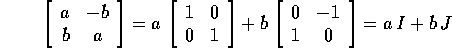
Il sottospazio 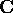è generato da I,J, dove I è la matrice
identità e J la matrice antisimmetrica definita sopra. In questa
rappresentazione matriciale del numero complesso , la
scelta di J, che determina la struttura complessa , deve
rispettare il requisito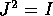 
. Ogni
matrice di 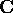è quindi presentabile in tre forme: come matrice,
come combinazione lineare della base 
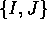e come coppia di
coordinate rispetto alla base:
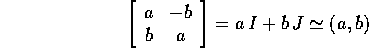
La forma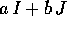 
dà la
rappresentazione algebrica del numero complesso ;
la forma (a,b) dà la
rappresentazione cartesiana del numero complesso
(nel cosiddetto piano di Argand-Gauss ).
L'insieme 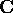di matrici non solo è chiuso rispetto
all'addizione e alla moltiplicazione per uno scalare, ma anche rispetto
al prodotto di matrici. Infatti
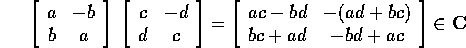
Il fatto più notevole a proposito del prodotto in è che
essa gode della proprietà commutativa:
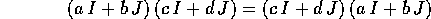
che non vale in generale per le matrici quadrate qualsiasi.
Il generatore I è l'unità reale ed il generatore
J l'unità immaginaria: se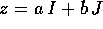 
, allora 
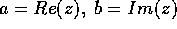. Il sottospazio di generato da I contiene i numeri
complessi che possono essere identificati con i numeri reali,
tramite la corrispondenza biunivoca tra 
e
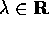; si usa perciò dire che 
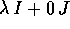è
un numero reale. Questa identificazione consente anche di scrivere
semplicemente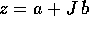 
, dove si sottintende l'unità reale.
L'uso anche contemporaneo delle diverse rappresentazioni dei
numeri complessi è possibile senza contraddizioni. Si possono per
esempio mescolare due modelli di numeri complessi ottenendo una
definizione consistente di prodotto; se infatti z=x+Jy, w=u+Jv,
possiamo eseguire il prodotto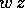 
usando per w la
rappresentazione come matrice, e la rappresentazione cartesiana
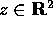, pur di considerare z come vettore colonna, ed usando
il prodotto di matrici riga per colonna:
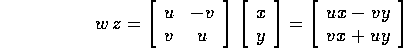
Poiché per ogni matrice di :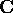
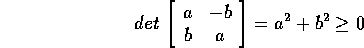
definiamo, per ogni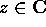 
, il modulo di z come 
.
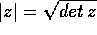Il modulo così definito ha le stesse proprietà della
lunghezza di un vettore:
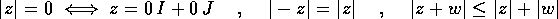
In effetti, se consideriamo la forma cartesiana del numero
complesso, cioè z=(x,y), allora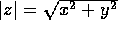 
, ossia il
modulo del numero complesso è la lunghezza del vettore che lo
rappresenta nel piano di Argand-Gauss. D'altro canto se z=(a,0)
è un numero complesso che è anche reale, |z|=|a|, cioè i due
usi dello stesso simbolo (e della stessa parola ``modulo") non
portano ad alcuna contraddizione.
Poiché il modulo di un numero complesso è la distanza dall'origine nel piano di Argand-Gauss, ossia il raggio delle coordinate polari, vogliamo definire la variabile angolo che assieme ad essa forma le coordinate polari. Se |z|=r>0, esiste una ed una sola matrice di rotazione tale che
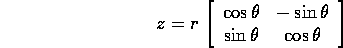
Infatti
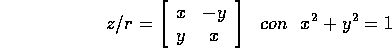
e usando la parametrizzazione della circonferenza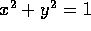 
mediante
seno e coseno si ottiene la matrice di rotazione. Allora ciascuno degli
angoli 
di rotazione della matrice z/r si chiama
argomento del numero complesso z, e si indica con arg(z).
Il modulo del prodotto è il prodotto dei moduli; gli argomenti
del prodotto sono la somma degli argomenti. Infatti dati 
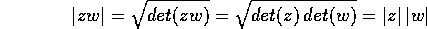
per il teorema del determinante del prodotto. Se poi
con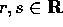 
, allora, eseguendo il prodotto
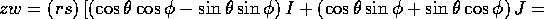
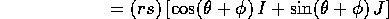
L'ultimo passaggio si può giustificare in due modi: o con
le formule di addizione della trigonometria, o perché
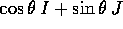è la matrice associata ad una
rotazione dell'angolo (in verso antiorario),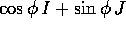 
è la matrice associata alla rotazione di 
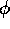, e
la composizione di due rotazioni è la rotazione dell'angolo somma.
In altre parole, non occorre ricordare le formule di addizione se ci
si ricordano le regole per moltiplicare i numeri complessi (che poi
discendono semplicemente dalle regole IJ=JI=J, JJ=-I).
Data 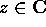, chiamiamo complesso coniugato di z, e
indichiamo con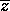 
, la matrice trasposta di z (che è
pure in ):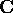
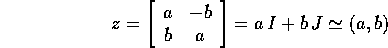
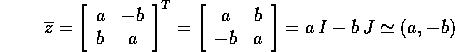
Il complesso coniugato ha la stessa parte reale Re(z), e parte
immaginaria opposta -Im(z). Ha quindi anche lo stesso modulo |z|,
ed argomenti opposti -arg(z). Vale la proprietà:
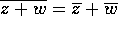. Anche per il prodotto:
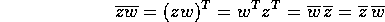
L'inverso di , 
, si può calcolare come
Infatti
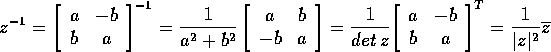
Seguono dalla formula dell'inverso le proprietà:
La potenza n-esima di un numero complesso z è definita per
induzione nello stesso modo della potenza di un numero reale:
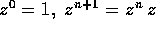. Usando la formula del modulo del prodotto
e dell'argomento del prodotto si mostra che
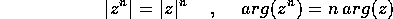
Si noti che le formule del modulo e dell'argomento della potenza
valgono per ogni n intero, anche negativo, purché naturalmente si
intenda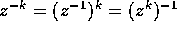 
.
Sia 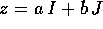una matrice di . Allora le radici
dell'equazione caratteristica , cioè i valori di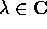 
tali che
sono i numeri complessi z e 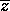. Infatti sia Re(z)=a, Im(z)=b:
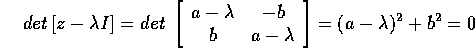
ha soluzione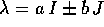 
. Questo è un caso
particolare del teorema di Hamilton-Cayley .
Consideriamo ora un sistema dinamico lineare con matrice non diagonalizzabile (in campo reale) di questo tipo:
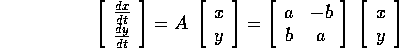
e costruiamo una variabile complessa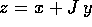 
; poiché come
già osservato si possono mescolare le due rappresentazioni
matriciali e vettoriali, ponendo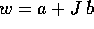 
il secondo membro
dell'equazione differenziale si può esprimere come prodotto in :
dove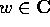 
è la stessa cosa di A considerata come numero complesso;
allora la soluzione si ottiene mediante la
funzione esponenziale di argomento complesso, che è definita dalla serie:
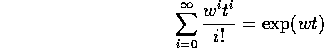
la cui convergenza è garantita dal teorema di
convergenza in norma , usando il modulo del numero
complesso come norma. Se la condizione iniziale è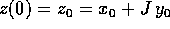 
:
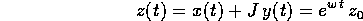
da cui la soluzione nel senso reale:
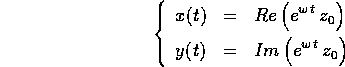
L'ambiguità nell'espressione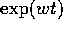 
, tra la funzione
esponenziale di una variabile complessa e l'esponenziale di matrice,
non crea alcun problema. In effetti le due serie coincidono, e la
loro convergenza può essere dimostrata indifferentemente usando il
modulo |wt| o la norma di matrice ||wt|| nel teorema di
convergenza in norma .
Esempio:
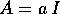corrisponde ad un numero complesso con
parte immaginaria 0, allora
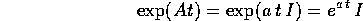
e le soluzioni del sistema dinamico sono semplicemente:
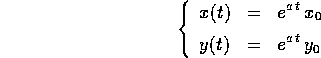
Esempio:
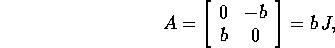
cioè corrisponde ad un numero immaginario puro, allora le potenze pari sono reali:
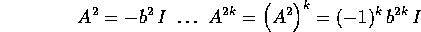
mentre le potenze dispari sono antisimmetriche, cioè immaginarie:
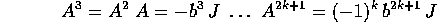
perciò le ridotte della serie esponenziale hanno un'espressione che si può calcolare esplicitamente:
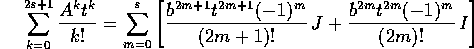
Ora il passaggio da fare con cautela è il riordino della serie, separando la parte di grado pari (quindi reale) da quella di grado dispari (quindi immaginaria). Questo è lecito perché la serie converge assolutamente, come si deduce dalla convergenza assoluta delle due serie separate per parte reale ed immaginaria:
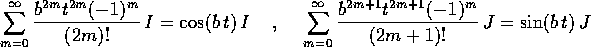
da cui si deduce la formula di Eulero :
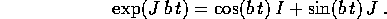
Applicando la formula dell'esponenziale di matrice per descrivere la soluzione del sistema dinamico in questo caso si ottiene:
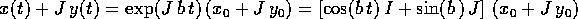
e separando parte reale e parte immaginaria:
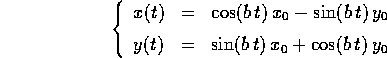
cioè la
soluzione, nota per via elementare, dell'esempio
dell'oscillatore armonico , con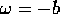 
.
Per trattare il caso generale dell'equazione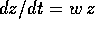 
con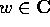
occorre utilizzare il teorema della somma degli esponenti :
poiché le due matrici I,J commutano tra loro (IJ=JI=J):
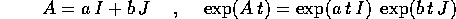
e quindi usando i calcoli eseguiti nei due esempi precedenti:
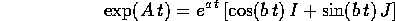
Allora le soluzioni di 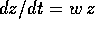dove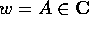 
sono le seguenti:
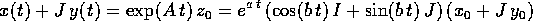
e per ottenere le soluzioni in forma reale basta moltiplicare ed separare parte reale e parte immaginaria:
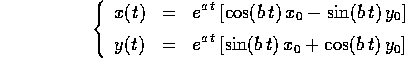
Il flusso integrale al tempo t si può descrivere come una rotazione
di un angolo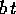 
seguita da un'omotetia di un fattore 
.
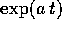Vorremmo generalizzare questa soluzione al caso di una arbitraria
matrice A di tipo 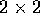con autovalori complessi coniugati
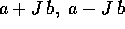. Consideriamo A come operatore lineare su 
;
allora esistono in due autovettori:
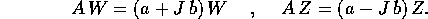
Gli autovettori relativi ai due autovalori coniugati
possono essere scelti in modo da essere coniugati tra loro:
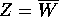; infatti, poiché A è reale, 
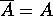e
quindi:
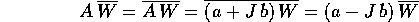
Consideriamo in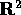 
i due vettori
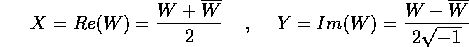
Il simbolo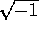 
è stato usato al posto di J per
evitare confusione tra le operazioni matriciali e le operazioni
algebriche in .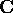
Allora riscriviamo le equazioni degli autovalori in termini di X,Y:
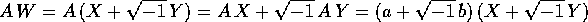
Ora basta eseguire la moltiplicazione e separare parte reale e parte immaginaria:
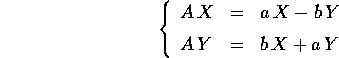
Supponiamo di usare un sistema di riferimento definito dalla base
. Sarebbe necessario verificare che i due vettori X,Y sono
linearmente indipendenti. La stessa applicazione associata ad A
con la base canonica diventa associata nella nuova base a Q:
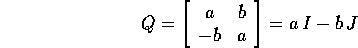
Perciò se si vuole calcolare
l'esponenziale di matrice di A, si può calcolare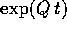 
che
è data dalla formula del caso precedente, e poi usare:
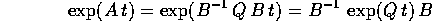
dove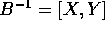 
è ottenuta per accostamento di colonne che
sono i vettori della nuova base.
In conclusione, se una matrice ha autovalori
complessi coniugati, è sempre possibile riportarla con un
cambiamento di riferimento ad una matrice che appartiene a 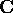, e
che corrisponde ad uno degli autovalori.
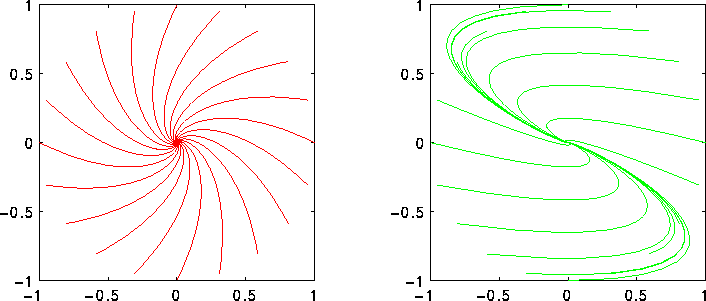
Figure 2.3: Un punto di equilibrio di tipo fuoco; a sinistra in forma canonica.
Figure 2.4: Un punto di equilibrio di tipo centro; a sinistra in forma canonica.
Possiamo quindi studiare il comportamento qualitativo nel caso in forma canonica
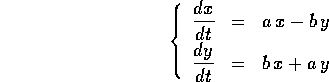
Il comportamento qualitativo delle soluzioni dipende solo dal segno di a:
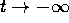e tendono al
punto di equilibrio nell'origine per
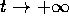. Le traiettorie sono
delle spirali, che si avvolgono attorno al punto di equilibrio con
frequenza pari alla parte immaginaria b.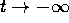 , cioè sono delle spirali che si svolgono, anziché
avvolgersi come nel caso precedente. Il punto di equilibrio si dice
di tipo fuoco , sia in questo caso che nel precedente.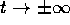
non esistono. Il punto di equilibrio si dice di tipo
centro . Si noti che per b>0 la rotazione attorno al punto di
equilibrio è in senso antiorario, al contrario di quello che si
ottiene nel caso dell'oscillatore armonico . In questo caso
il sistema dinamico ammette un integrale primo
.
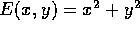Problema
Nel piano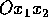 
determinare tutte le curve
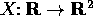, la cui tangente nel punto P forma un angolo
costante 
con OP. Per quali le curve sono
limitate ?
(Soluzione)
Definizione:
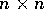a coefficienti reali, si dice
matrice semisemplice se è diagonalizzabile in senso complesso,
cioè se esiste una base di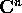 
formata di autovettori
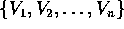, cioè tale che:
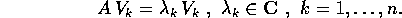
Una matrice con tutti gli autovalori, reali o complessi, semplici (nel senso di molteplicità algebrica 1) è certamente semisemplice, perché gli autovettori corrispondenti ad autovalori diversi sono sempre linearmente indipendenti, e per il teorema fondamentale dell'algebra gli autovalori sono esattamente n. Però una matrice può essere semisemplice anche con degli autovalori multipli.
Teorema del sistema semisemplice : Se la matrice A è semisemplice, allora tutte le orbite del sistema dinamico:
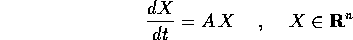
si possono esprimere mediante combinazioni lineari di funzioni esponenziali
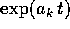(dove gli 
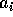sono le parti reali degli autovalori di A)
moltiplicate per funzioni trigonometrich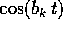e 
e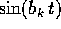 
(dove i 
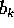sono le parti immaginarie degli autovalori di A).
Dimostrazione:
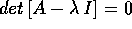è
un'equazione algebrica, di grado n se A è di tipo ,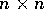
ed a coefficienti reali che sono gli invarianti della matrice.
Perciò essa ha n radici, contate con la loro molteplicità, tra cui
alcune saranno reali:
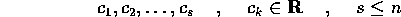
e altre saranno a coppie complesse coniugate:
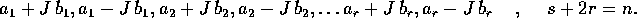
Anche se alcune radici sono ripetute, per ipotesi A è semisemplice e quindi per ogni autovalore c'è un autovettore, in modo che ce ne siano n=s+2r tra loro linearmente indipendenti. Perciò per gli autovalori reali:
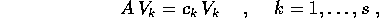
e per quelli complessi:
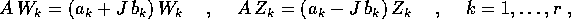
dove gli autovettori relativi a due autovalori
complessi coniugati possono essere scelti in modo da essere
coniugati tra loro: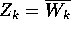 
, per lo stesso ragionamento
fatto sopra nel caso di una sola coppia.
Sarebbe necessario verificare
che questa scelta mantiene l'indipendenza lineare su degli
autovettori.
Prendiamo ora una base di 
costituita dai
seguenti vettori reali:
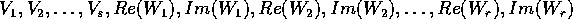
Sarebbe necessario verificare che questa è una base; per esempio la
parte reale del sottospazio generato da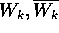 
è
generata da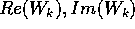 
.
Scriviamo la matrice Q che esprime la stessa applicazione lineare di
A, rispetto alla base così definita. Poiché nella nuova base
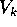è espresso in componenti come il vettore 
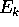della base canonica
(con tutte le componenti 0 salvo la k-esima uguale a 1):
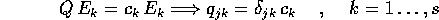
da cui si deduce che le prime s colonne della matrice Q sono quelle di una matrice diagonale, con gli autovalori reali sulla diagonale principale.
Consideriamo ora la coppia di vettori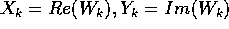 
che
compaiono nella base al posto s+2k-1, s+2k, e perciò sono
rappresentati in componenti nel nuovo sistema di riferimento da
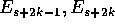: ripetendo lo stesso ragionamento del caso
con una sola coppia di autovalori coniugati :
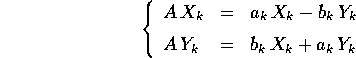
e quindi la matrice Q del nuovo sistema di riferimento ha questo effetto:
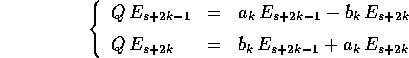
il che vuol dire che nelle colonne s+2k-1, s+2k della matrice
Q i coefficienti sono tutti zero salvo quelli della sottomatrice
vicino alla diagonale, la quale è:
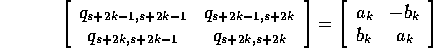
Per ogni coppia di autovalori complessi coniugati, nella
matrice trasformata al nuovo sistema di riferimento appare un
blocco 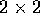che è in 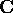, e corrisponde ad uno dei due
autovalori in questione.
In conclusione la matrice A può
essere trasformata per coniugio nella ma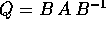trice 
dove
la matrice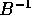 
è formata dai vettori colonna della nuova
base; la matrice Q ha sulla diagonale principale gli autovalori
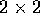reali e in blocchi vicino alla diagonale principale gli
autovalori complessi. Esprimiamo questa forma speciale della matrice Q
con la notazione diagonale a blocchi :
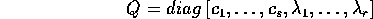
con la convenzione che ogni autovalore complesso
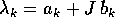sia descritto dal suo blocco .
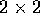Una matrice Q di questa forma si chiama
forma canonica di un semisemplice .
Allora l'esponenziale
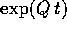sarà diagonale a blocchi, cioè data da un'espressione
formalmente analoga a quella dell'esponenziale di una matrice
diagonale:
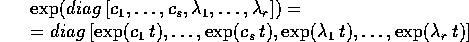
dove l'esponenziale di un numero reale è la funzione
esponenziale, e l'esponenziale di un numero complesso è
l'esponenziale complessa rappresentata da una matrice :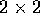
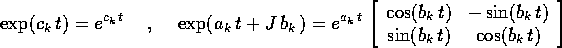
La dimostrazione è conclusa con l'esame della formula usuale:
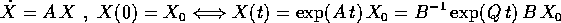
Esercizio Determinare il flusso integrale del sistema dinamico
