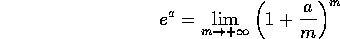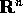 è una funzione
è una funzione 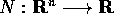 che soddisfa, per ogni
che soddisfa, per ogni 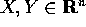 e
e
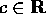 , alle tre proprietà seguenti:
, alle tre proprietà seguenti:
Sommario Vogliamo dimostrare la convergenza della serie esponenziale di matrici, usando risultati noti sulle serie assolutamente convergenti. Le proprietà della funzione esponenziale sono conservate dall'esponenziale di matrici purché non dipendano dalla proprietà commutativa della moltiplicazione: in particolare l'esponenziale della somma è uguale al prodotto delle esponenziali solo se il prodotto commuta.
Definizione:
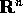 è una funzione
è una funzione 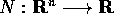 che soddisfa, per ogni
che soddisfa, per ogni 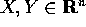 e
e
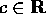 , alle tre proprietà seguenti:
, alle tre proprietà seguenti:
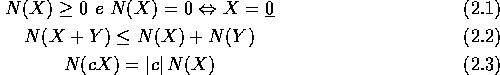
Esempio:
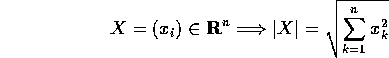
ed è legata al prodotto scalare: 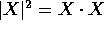 .
Per verificare la diseguaglianza triangolare
.
Per verificare la diseguaglianza triangolare 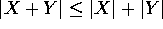 si
usa la diseguaglianza di Cauchy :
si
usa la diseguaglianza di Cauchy :
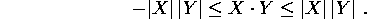
Esempio:
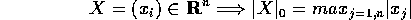
Esempio:
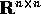 delle matrici
quadrate
delle matrici
quadrate 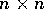 . Ogni matrice A si può anche considerare
come un operatore lineare su
. Ogni matrice A si può anche considerare
come un operatore lineare su 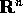 . Allora possiamo associare ad
A la norma uniforme dell'operatore lineare:
. Allora possiamo associare ad
A la norma uniforme dell'operatore lineare:

Il massimo esiste perché la sfera |X|=1 di 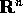 è un
compatto . Oltre alle tre proprietà che fanno parte
della definizione di norma (e che dovrebbero essere verificate), la
norma uniforme soddisfa anche alle seguenti:
è un
compatto . Oltre alle tre proprietà che fanno parte
della definizione di norma (e che dovrebbero essere verificate), la
norma uniforme soddisfa anche alle seguenti:

Si potrebbe definire la norma
uniforme anche a partire da un'altra norma di 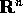 diversa da
quella euclidea, usando le stesse formule con N(X) al posto di
|X|; tutte le sei proprietà citate sopra sarebbero comunque
valide.
diversa da
quella euclidea, usando le stesse formule con N(X) al posto di
|X|; tutte le sei proprietà citate sopra sarebbero comunque
valide.
Per il teorema di equivalenza delle norme , tutte le norme
su spazi vettoriali di dimensione finita sono equivalenti, quindi
anche la norma uniforme delle matrici ||A|| è equivalente alla
norma euclidea di 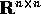 , e anche alla norma del massimo di
, e anche alla norma del massimo di
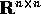 . Quindi la convergenza in norma uniforme e la
convergenza di ogni coefficiente delle matrici sono equivalenti (vedi
Sezione B.4).
. Quindi la convergenza in norma uniforme e la
convergenza di ogni coefficiente delle matrici sono equivalenti (vedi
Sezione B.4).
Problema Dimostrare le 6 proprietà (2.1)-(2.6) per la norma uniforme ||A||. (Soluzione)
La convergenza dell'esponenziale di matrice può essere dimostrata come conseguenza della convergenza in norma della serie.
Teorema di convergenza dell'esponenziale di matrici :
Sia A una qualsiasi matrice quadrata 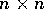 . Allora la serie
esponenziale:
. Allora la serie
esponenziale:
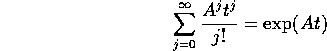
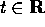 ,
uniformemente su ogni compatto di
,
uniformemente su ogni compatto di 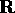 .
.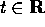 , che indichiamo con
, che indichiamo con 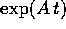 .
.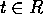 da:
da:
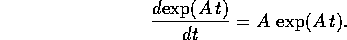
Dimostrazione:

Usando la diseguaglianza che segue dalle proprietà della norma uniforme:
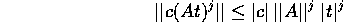
si ottiene una nuova serie numerica che maggiora termine a termine la serie delle norme:
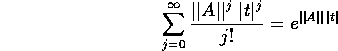
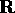 ) perché coincide con la
serie di Taylor della funzione esponenziale di argomento scalare
) perché coincide con la
serie di Taylor della funzione esponenziale di argomento scalare
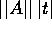 ; a maggior ragione la serie esponenziale di matrice
converge in norma. Applicando il teorema
di convergenza in norma ne segue
la convergenza della serie esponenziale di matrice.
; a maggior ragione la serie esponenziale di matrice
converge in norma. Applicando il teorema
di convergenza in norma ne segue
la convergenza della serie esponenziale di matrice.
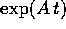 , essendo limite di
una serie uniformemente convergente di funzioni continue della
variabile t, è una funzione continua su ogni compatto
contenuto in
, essendo limite di
una serie uniformemente convergente di funzioni continue della
variabile t, è una funzione continua su ogni compatto
contenuto in 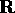 , perciò è una funzione continua in ogni
, perciò è una funzione continua in ogni
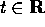 .
.
Questo teorema basta a dimostrare l'esistenza del flusso
integrale di un qualsiasi sistema dinamico continuo lineare 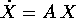 , che è la somma della serie convergente
, che è la somma della serie convergente 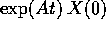 . Però calcolare esplicitamente tale soluzione non è
immediato. Il procedimento di calcolo sarà spiegato nelle
Sezioni 2.3, 2.4,
2.5.
. Però calcolare esplicitamente tale soluzione non è
immediato. Il procedimento di calcolo sarà spiegato nelle
Sezioni 2.3, 2.4,
2.5.
Problema Dimostrare che se A è una matrice quadrata con ||A||<1 allora la serie

converge a 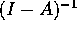 .
(Soluzione)
.
(Soluzione)
Consideriamo due serie di matrici convergenti, della forma:
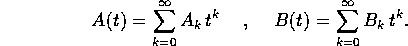
Vogliamo sapere sotto quali condizioni si potrà ricavare dalle due
serie con somme A(t) e B(t) una serie con per somma il prodotto di
matrici 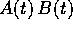 .
.
La dipendenza dalla variabile t non è veramente essenziale in questo ragionamento, che può essere svolto sostituendo t=1; ma come vedremo questa semplificazione renderebbe meno comprensibile il procedimento.
Definizione:
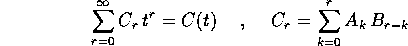
Questa definizione si ottiene riordinando le somme parziali del prodotto delle due serie secondo il grado in t.
Le condizioni di convergenza della serie, ad una funzione continua C(t), sono descritte dal teorema del prodotto secondo Cauchy .
Per l'applicazione che ci interessa, basta sapere che se le
due serie per A(t), B(t) convergono in norma per ogni 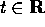 ,
allora la serie prodotto converge in norma, quindi anche converge per
ogni
,
allora la serie prodotto converge in norma, quindi anche converge per
ogni 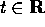 , e la sua somma
, e la sua somma 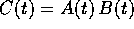 .
.
Teorema della somma degli esponenti :
Se due matrici quadrate 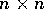 , A e B, commutano tra
loro, cioè
, A e B, commutano tra
loro, cioè 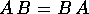 , allora l'esponenziale della somma è il
prodotto delle esponenziali:
, allora l'esponenziale della somma è il
prodotto delle esponenziali:
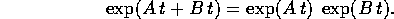
Dimostrazione:
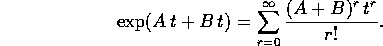
Poiché le due matrici commutano, si può usare la formula del binomio di Newton :

sostituendo nella serie dell'esponenziale della somma, e riordinando i termini, il che è lecito poiché la serie è assolutamente convergente:
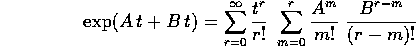
e si ottiene esattamente la serie prodotto secondo Cauchy delle due serie esponenziali; poiché tutte queste serie sono convergenti in norma, usando il teorema delprodotto secondo Cauchy si ricava:
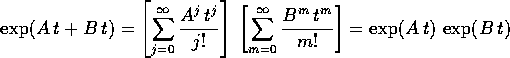
Teorema di derivazione dell'esponenziale :
La funzione a valori matriciali 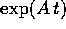 è derivabile, e la
sua derivata è:
è derivabile, e la
sua derivata è:
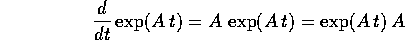
Dimostrazione:
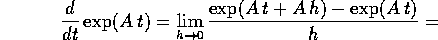
per il teorema della somma degli esponenti:
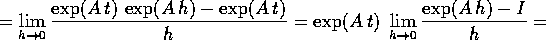
ora usiamo la serie esponenziale per espandere in potenze dell'incremento h:
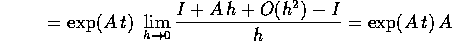
Resta da verificare che A commuta con 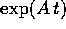 ; in effetti A
commuta con
; in effetti A
commuta con 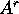 , quindi anche con ogni addendo della serie
esponenziale, e poiché la moltiplicazione di matrici è
un'operazione continua, la relazione di commutazione passa al
limite.
, quindi anche con ogni addendo della serie
esponenziale, e poiché la moltiplicazione di matrici è
un'operazione continua, la relazione di commutazione passa al
limite.
Problema Si dimostri l'eguaglianza:
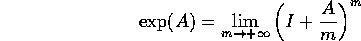
che costituisce una definizione alternativa dell'esponenziale di matrici.
Suggerimento: scrivere la differenza
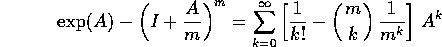
che è corretta se si considera che i coefficienti binomiali sono nulli quando k>m; la serie a secondo membro ha coefficienti non negativi, e se si passa alle norme ci si riconduce alla dimostrazione che