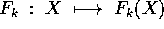 , definite su
, definite su
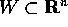

si dice uniformemente convergente su W alla funzione F(X)
se, per ogni  , esiste un intero m tale che
, esiste un intero m tale che
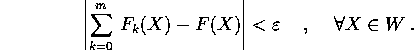
Definizione:
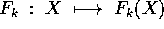 , definite su
, definite su
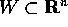

si dice uniformemente convergente su W alla funzione F(X)
se, per ogni  , esiste un intero m tale che
, esiste un intero m tale che
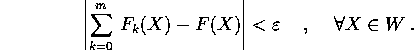
Una serie di potenze è una serie di funzioni ciascuna rappresentata da un monomio: per esempio in una sola variabile x

ogni serie di potenze ha un raggio di convergenza r tale che per
|x|<r la serie converge ad una funzione f(x), e converge
uniformemente su ogni insieme della forma 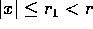 ; non è
escluso il caso in cui
; non è
escluso il caso in cui 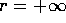 (come per la serie esponenziale).
Questo si ottiene applicando il teorema seguente:
(come per la serie esponenziale).
Questo si ottiene applicando il teorema seguente:
Teorema di convergenza in norma : Se una serie

dove i termini 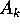 sono vettori di
sono vettori di 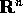 (anche
(anche 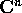 , o
matrici) converge in norma, cioè esiste una norma
, o
matrici) converge in norma, cioè esiste una norma 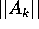 per
cui la serie numerica
per
cui la serie numerica

è convergente, allora anche la serie è convergente.
Questo teorema in sostanza equivale all'affermazione che lo
spazio 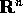 (o
(o 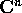 ) è uno spazio metrico completo .
) è uno spazio metrico completo .
Teorema di derivazione per serie : All'interno del raggio di convergenza, la serie converge ad una funzione f(x) derivabile, e la derivata è la somma della serie ottenuta derivando termine a termine
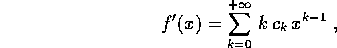
che ha lo stesso raggio di convergenza.
Teorema del prodotto secondo Cauchy : Date due serie di potenze, se esse sono convergenti e convergenti in norma:
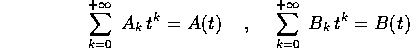
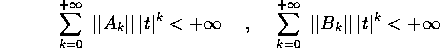
allora la loro serie prodotto secondo Cauchy è convergente
in norma, e converge alla funzione prodotto 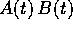 .
.
Teorema di completezza delle funzioni continue : Una serie di funzioni continue su di un compatto , che sia di Cauchy (nel senso della metrica della convergenza uniforme ) converge uniformemente sul compatto stesso. Una serie uniformemente convergente di funzioni continue ha per limite una funzione continua.
Un altro tipo notevole di serie di funzioni è una serie di Fourier : per esempio in una variabile x
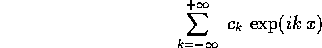
con coefficienti di Fourier complessi 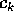 , oppure
, oppure
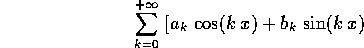
con coefficienti di Fourier reali 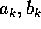 . Ogni funzione
. Ogni funzione 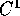 e
periodica di periodo
e
periodica di periodo 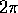 nella variabile x è somma di una serie
di Fourier uniformemente convergente. L'analogo multidimensionale
riguarda le funzioni
nella variabile x è somma di una serie
di Fourier uniformemente convergente. L'analogo multidimensionale
riguarda le funzioni 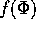 di n variabili angolo, quindi con
di n variabili angolo, quindi con
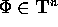 , che sono pure ottenibili come somma di una serie di Fourier
uniformemente convergente
, che sono pure ottenibili come somma di una serie di Fourier
uniformemente convergente
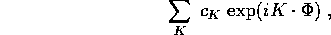
dove la somma è estesa a tutti i multiindici
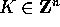 .
.
Bibliografia :