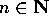 e
e 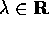 , indichiamo con
, indichiamo con
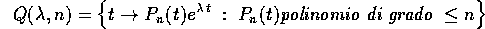
l'insieme dei quasipolinomi con esponente  e di grado
fino ad n.
e di grado
fino ad n.
Sommario L'operatore di derivazione, e le combinazioni lineari di derivazioni che appaiono nei primi membri delle equazioni differenziali lineari a coefficienti costanti , sono applicazioni lineari tra spazi di funzioni, che sono spazi vettoriali di dimensione infinita. Quando le equazioni differenziali lineari a coefficienti costanti non sono omogenee , si può dimostrare l'esistenza delle soluzioni ma di solito non è agevole calcolarle esplicitamente. Se si riesce a considerare la restrizione di un operatore differenziale ad un sottospazio di dimensione finita, il problema è ricondotto ad un sistema di equazioni lineari nelle coordinate rispetto ad una base di questo spazio. La scelta del sottospazio di dimensione finita non è però arbitraria: esso deve contenere non solo il secondo membro, ma anche il nucleo dell'operatore; siamo perciò condotti a studiare gli spazi di quasipolinomi.
Definizione:
L' insieme dei quasipolinomi con esponente dato e grado limitato
è un sottospazio vettoriale dello spazio a
dimensione infinita delle funzioni 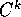 (con k abbastanza grande).
Il teorema delle soluzioni dell'equazione a coefficienti costanti
assicura che ogni equazione di questo tipo, omogenea, ha soluzioni che
sono combinazioni lineari di quasipolinomi, purché le radici del
polinomio caratteristico siano reali.
(con k abbastanza grande).
Il teorema delle soluzioni dell'equazione a coefficienti costanti
assicura che ogni equazione di questo tipo, omogenea, ha soluzioni che
sono combinazioni lineari di quasipolinomi, purché le radici del
polinomio caratteristico siano reali.
Niente impedisce di considerare quasipolinomi con un esponente
 complesso, e con coefficienti dei polinomi pure complessi,
come si vedrà nel metodo delle ampiezze complesse . Il
teorema delle
soluzioni dell'equazione a coefficienti costanti
ci assicura che tutte le soluzioni delle equazioni omogenee
sono in ogni caso combinazioni lineari di quasipolinomi, pur di
considerare coefficienti complessi coniugati per i quasipolinomi
complessi in
complesso, e con coefficienti dei polinomi pure complessi,
come si vedrà nel metodo delle ampiezze complesse . Il
teorema delle
soluzioni dell'equazione a coefficienti costanti
ci assicura che tutte le soluzioni delle equazioni omogenee
sono in ogni caso combinazioni lineari di quasipolinomi, pur di
considerare coefficienti complessi coniugati per i quasipolinomi
complessi in 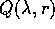 e
e 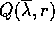 dove
dove 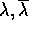 siano radici del polinomio caratteristico.
siano radici del polinomio caratteristico.
È immediato verificare che
l'operatore di derivazione D trasforma 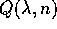 in se stesso:
in se stesso:
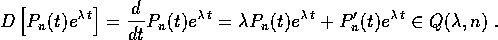
Poiché la restrizione dell'operatore di derivazione a 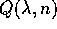 è un'applicazione lineare tra spazi vettoriali di dimensione finita,
basta scegliere una base per trovare una matrice associata:
è un'applicazione lineare tra spazi vettoriali di dimensione finita,
basta scegliere una base per trovare una matrice associata:
Teorema della derivazione sui quasipolinomi : L'operatore lineare
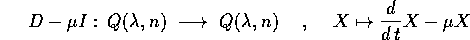
è invertibile per 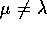 , nilpotente (di rango n+1-1=n)
per
, nilpotente (di rango n+1-1=n)
per 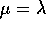 .
.
Dimostrazione:
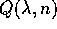 è uno spazio vettoriale reale di dimensione n+1, e le
funzioni
è uno spazio vettoriale reale di dimensione n+1, e le
funzioni
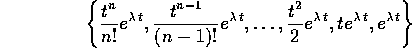
ne costituiscono una base, rispetto alla quale l'endomorfismo lineare d/dt è rappresentato dalla matrice
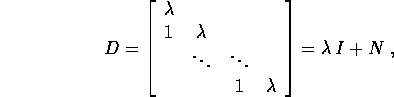
con N nilpotente di ordine n+1. Perciò per 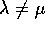 l'operatore
l'operatore 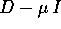 è invertibile, per
è invertibile, per 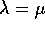 si riduce alla parte nilpotente con un solo
blocco di Jordan .
si riduce alla parte nilpotente con un solo
blocco di Jordan .
Il teorema della derivazione sui quasipolinomi ha immediata
applicazione alla risoluzione di un'equazione differenziale lineare di
ordine n a coefficienti costanti che sia non omogenea ,
cioè con secondo membro una funzione assegnata. Per ogni
funzione 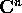 x(t), sia P(D) l'operatore differenziale lineare
definito dal polinomio
x(t), sia P(D) l'operatore differenziale lineare
definito dal polinomio 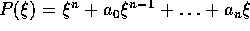 come
come
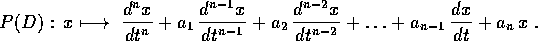
Teorema dell' isomorfismo tra quasipolinomi :
Se 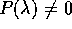 , l'operatore
, l'operatore
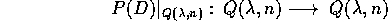
è un isomorfismo lineare per ogni 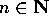 .
.
Dimostrazione:
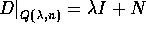 segue
segue
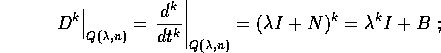
dove B è una matrice con coefficienti non nulli solo sotto la
diagonale. Allora l'operatore P(D) ristretto a 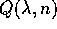 è
associato alla matrice
è
associato alla matrice
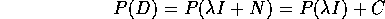
dove C ha pure coefficienti non nulli solo sotto la diagonale.
Perciò P(D) ha sulla diagonale principale coefficienti tutti
uguali a 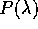 , e
, e 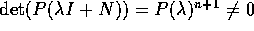 , ossia P(D) è invertibile.
, ossia P(D) è invertibile.
Teorema dell' abbassamento di grado dei quasipolinomi :
Se  è una radice di
è una radice di 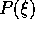 di molteplicità r, cioè
se
di molteplicità r, cioè
se
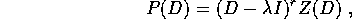
essendo Z un polinomio con 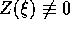 , allora
, allora
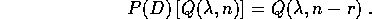
Dimostrazione:
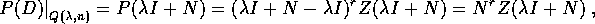
con 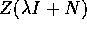 un isomorfismo lineare, che conserva il grado (per
il teorema dell'isomorfismo tra quasipolinomi ). Invece
un isomorfismo lineare, che conserva il grado (per
il teorema dell'isomorfismo tra quasipolinomi ). Invece
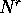 lo abbassa di r: su ogni elemento della base N agisce così:
lo abbassa di r: su ogni elemento della base N agisce così:
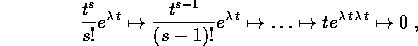
quindi per s>r
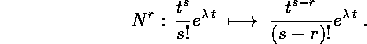
I due teoremi suggeriscono la forma delle soluzioni di
un'equazione del tipo 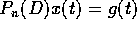 in cui il termine ``forzante''
g(t) è del tipo
in cui il termine ``forzante''
g(t) è del tipo 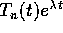 , con
, con 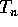 polinomio di grado n.
polinomio di grado n.
Infatti, come si verifica facilmente, applicando l'operatore P(D)
alla funzione 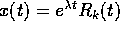 , dove
, dove 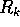 è un polinomio di grado k, si ottiene
è un polinomio di grado k, si ottiene
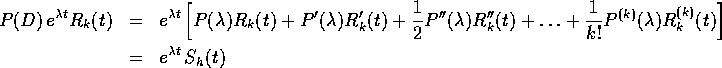
per un certo polinomio 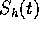 di grado h.
Quindi P(D) trasforma un quasipolinomio di grado k in un
quasipolinomio con lo stesso esponente, ma con grado h che dipende
dall'ordine della prima derivata di P che non si annulla in
di grado h.
Quindi P(D) trasforma un quasipolinomio di grado k in un
quasipolinomio con lo stesso esponente, ma con grado h che dipende
dall'ordine della prima derivata di P che non si annulla in
 . Sia r è la molteplicità di
. Sia r è la molteplicità di  come radice di
P, allora
come radice di
P, allora
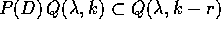 .
.
Quindi se, dato 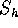 , si vuole ricostruire
, si vuole ricostruire 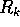 :
:
 non è radice di
non è radice di 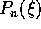 , la soluzione particolare è
un quasipolinomio in
, la soluzione particolare è
un quasipolinomio in 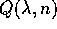 (si cerca un polinomio di grado n da
moltiplicare per
(si cerca un polinomio di grado n da
moltiplicare per 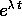 );
);
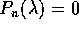 si calcola la
molteplicità algebrica r di
si calcola la
molteplicità algebrica r di  per
per 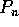 e si trova la
soluzione particolare in
e si trova la
soluzione particolare in 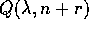 , con un polinomio
, con un polinomio
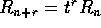 che resta individuato da n+1
coefficienti (mentre i polinomi di grado fino ad r-1
sono soluzioni dell'equazione omogenea).
che resta individuato da n+1
coefficienti (mentre i polinomi di grado fino ad r-1
sono soluzioni dell'equazione omogenea).
La soluzione generale dell'equazione non omogenea si può esprimere come somma di una soluzione particolare dell'equazione non omogenea e della soluzione generale dell'equazione omogenea; quest'ultima contiene le costanti arbitrarie che possono essere determinate in modo da soddisfare alle condizioni iniziali .
La regola precedente non ha niente di diverso da quella che si usa per risolvere un sistema lineare non omogeneo in uno spazio a dimensione finita; ed in effetti a questo ci siamo ricondotti. Il sistema lineare che lega le costanti arbitrarie alle condizioni iniziali ha matrice dei coefficienti uguale a quella del caso omogeneo, e differisce solo per il secondo membro; quindi anche in questo caso la soluzione è sempre unica.
Esercizio Risolvere l'equazione del quarto ordine
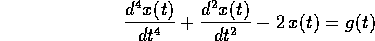
nei casi in cui 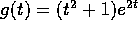 e
e
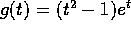 .
.
Estendiamo la definizione di quasipolinomio al caso con esponente complesso
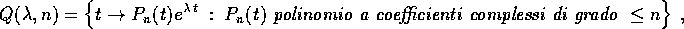
con 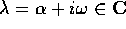 : ciò consente di risolvere anche
i sistemi dinamici lineari non omogenei in cui le componenti del
termine ``forzante'' contengono seni e coseni.
: ciò consente di risolvere anche
i sistemi dinamici lineari non omogenei in cui le componenti del
termine ``forzante'' contengono seni e coseni.
Si noti che in questo capitolo usiamo la notazione in cui ``i'' è l'unità immaginaria, per evitare confusione tra operazioni matriciali e il prodotto di uno scalare complesso per un vettore o matrice.
Supponiamo che il problema da risolvere sia un'equazione di ordine n non omogenea della forma

dove g(t) può essere considerata, senza perdita di generalità, del tipo
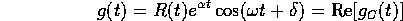
dove
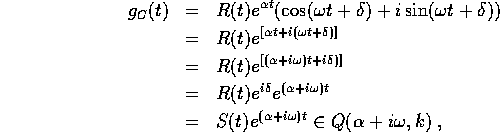
per R(t) polinomio reale e S(t) polinomio complesso di grado k;
allora si ottiene 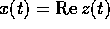 , dove z(t) è la soluzione
complessa dell'equazione
, dove z(t) è la soluzione
complessa dell'equazione
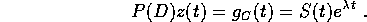
Nel caso particolare in cui 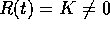 è costante e
è costante e
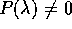 , per il teorema
dell'isomorfismo tra quasipolinomi esiste una
costante H per cui
, per il teorema
dell'isomorfismo tra quasipolinomi esiste una
costante H per cui 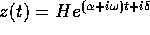 (metodo
delle ampiezze complesse ).
(metodo
delle ampiezze complesse ).
Infatti 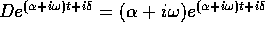 ; il valore di
; il valore di  che
risolve l'equazione con
che
risolve l'equazione con  si ricava da un'equazione
algebrica:
si ricava da un'equazione
algebrica:
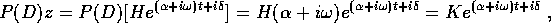
ossia:
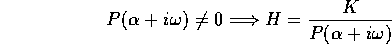
Passando alla rappresentazione esponenziale del numero complesso H,
cioè scrivendo 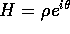 ,
,
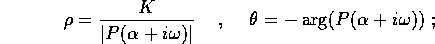
prendendo la parte reale si ottiene la soluzione particolare dell'equazione a coefficienti reali
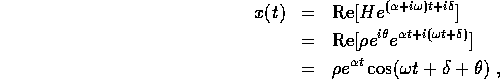
che permette di osservare lo sfasamento di un angolo  fra il
termine ``forzante'' g(t) e la risposta ``forzata'' x(t), la cui
intensità è proporzionale a quella di g(t).
fra il
termine ``forzante'' g(t) e la risposta ``forzata'' x(t), la cui
intensità è proporzionale a quella di g(t).
Il nome ``ampiezze complesse'' si spiega se si considera prima il caso in cui il secondo membro sia soltanto un coseno, ed il primo membro un oscillatore armonico; allora il coefficiente da determinare è l'ampiezza (reale) dell'oscillazione forzata.
Nel caso in cui 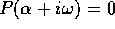 , invece, l'operatore
differenziale genera, nella soluzione dell'equazione omogenea,
termini con lo stessa frequenza
, invece, l'operatore
differenziale genera, nella soluzione dell'equazione omogenea,
termini con lo stessa frequenza  di g(t): si può verificare
così una risonanza fra l'operatore differenziale e il
termine forzante, e per determinare la soluzione z(t) si applica il
teorema dell'abbassamento di grado dei quasipolinomi .
di g(t): si può verificare
così una risonanza fra l'operatore differenziale e il
termine forzante, e per determinare la soluzione z(t) si applica il
teorema dell'abbassamento di grado dei quasipolinomi .
Esercizio Risolvere l'equazione del quarto ordine
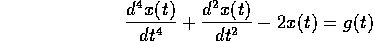
nei casi in cui
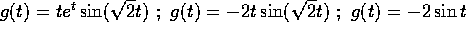 .
(Soluzione)
.
(Soluzione)
Esempio:
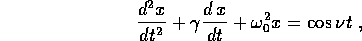
le cui soluzioni sono la parte reale delle soluzioni complesse di
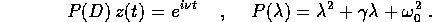
Allora, se 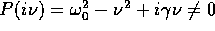 (sempre verificato se
(sempre verificato se
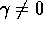 ),
),

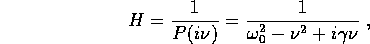
la soluzione dell'equazione omogenea (cioè
dell'oscillatore lineare ),
supponendo che 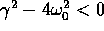 , in modo che
, in modo che 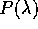 abbia radici complesse
abbia radici complesse 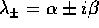 , è
, è
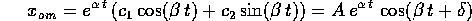
per costanti arbitrarie 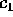 e
e 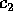 , oppure A e
, oppure A e 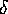 , mentre
la soluzione particolare dell'equazione non omogenea è
, mentre
la soluzione particolare dell'equazione non omogenea è
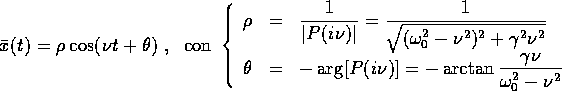
Se si calcola la costante complessa H usando il normale
procedimento di razionalizzazione delle frazioni con radicali (in
fondo l'unità immaginaria è appunto 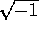 ), cioè usando
), cioè usando
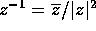 :
:
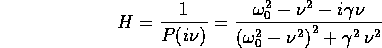
si vede che le soluzioni dell'oscillatore lineare forzato si possono scrivere usando solo le quattro operazioni aritmetiche.
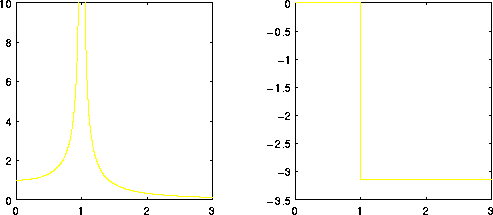
Figure 8.1: Risposta di un oscillatore armonico forzato: a
sinistra l'ampiezza dell'oscillazione forzata, a destra il ritardo di
fase, in funzione della frequenza forzante. In questo caso alla
frequenza 1 si ha risonanza.
Esempio:
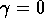 , abbiamo un
oscillatore armonico forzato . Allora
, abbiamo un
oscillatore armonico forzato . Allora

e, per 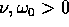 ,
,
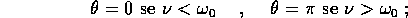
in tal caso
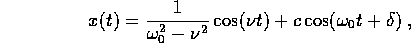
con c e 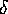 da determinare in base alle condizioni iniziali del
problema; l'ampiezza della risposta tende all'infinito alla
risonanza , cioè per
da determinare in base alle condizioni iniziali del
problema; l'ampiezza della risposta tende all'infinito alla
risonanza , cioè per 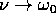 (si veda la
Figura 8.1). Si crea così un battimento :
indicando con
(si veda la
Figura 8.1). Si crea così un battimento :
indicando con  e B=c,
e B=c,
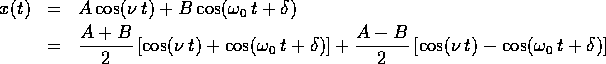
ed utilizzando le formule di prostaferesi:
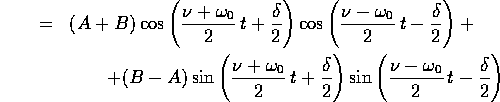
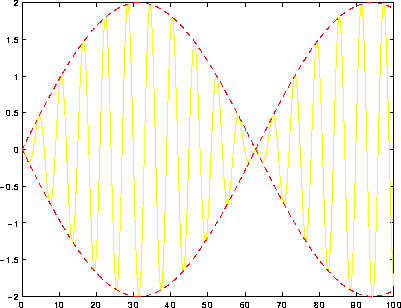
Figure 8.2: Nella soluzione dell'oscillatore armonico
forzato si ottiene un battimento. In particolare se la frequenza
forzante e quella di oscillazione propria sono molto vicine, la
soluzione appare come un'oscillazione con frequenza vicina ad
entrambe, la cui ampiezza oscilla a bassa frequenza.
In Figura 8.2 è tracciato un grafico di x(t) per
A=-B e 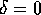 , con
, con 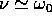 in modo da rendere la
frequenza
in modo da rendere la
frequenza 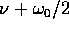 molto più alta di
molto più alta di 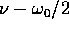 .
.
Esempio:
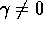 (caso
dell'oscillatore lineare smorzato ),
l'ampiezza della risposta è massima alla risonanza:
(caso
dell'oscillatore lineare smorzato ),
l'ampiezza della risposta è massima alla risonanza:
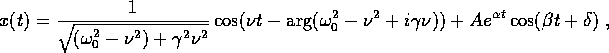
dove 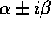 sono le radici di
sono le radici di
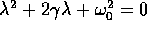
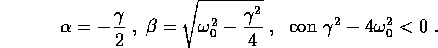
Qui 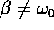 , per quanto
, per quanto 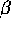 possa avvicinarsi a
possa avvicinarsi a
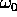 se
se 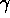 è molto piccolo.
è molto piccolo.
La risposta forzata ha un andamento illustrato nella Figura 8.3: l'ampiezza della oscillazione forzata, e lo sfasamento, sono dati da:
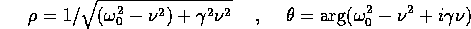
quindi
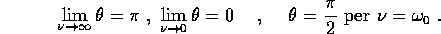
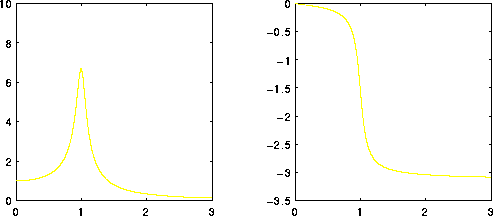
Figure 8.3: Risposta di un oscillatore lineare forzato: a
sinistra l'ampiezza dell'oscillazione forzata, a destra il ritardo di
fase, in funzione della frequenza forzante. Alla frequenza 1 si ha
risonanza, ma la risposta ha un'ampiezza finita, proporzionale
all'inverso della dissipazione.
La soluzione omogenea è un'oscillazione smorzata: se 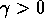 essa
tende a 0 (esponenzialmente) e diventa trascurabile dopo un tempo
abbastanza lungo (vedi Figura 8.3).
essa
tende a 0 (esponenzialmente) e diventa trascurabile dopo un tempo
abbastanza lungo (vedi Figura 8.3).
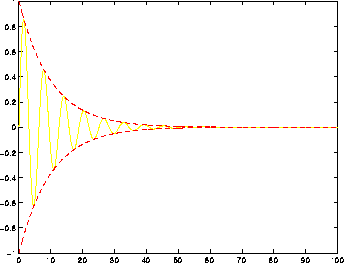
Figure 8.4: La soluzione omogenea di un oscillatore
lineare con dissipazione positiva si smorza rapidamente, in modo
esponenziale, e diventa trascurabile.
Nel caso in cui il termine forzante risuona con le soluzioni dell'equazione omogenea, cioè, in forma complessa,
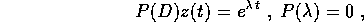
dalla teoria dei quasipolinomi si ricava la forma della soluzione particolare dell'equazione non omogenea

con una costante H da determinare.
Esempio:
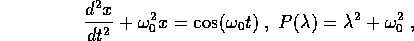
le radici di 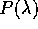 sono
sono 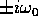 , e la forma complessa
dell'equazione è
, e la forma complessa
dell'equazione è

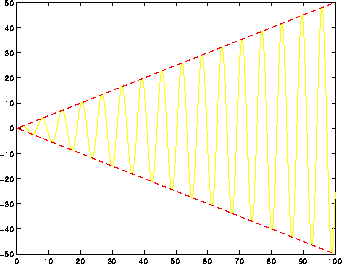
Figure 8.5: Soluzione di un oscillatore armonico alla
risonanza esatta tra forzante e oscillazioni proprie; in questa figura
si mostra solo la parte forzata, la cui ampiezza di oscillazione
cresce linearmente ed illimitatamente col tempo.
La soluzione particolare è 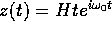 e la soluzione
generale è
e la soluzione
generale è
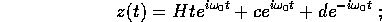
per determinare H
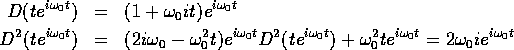
per cui 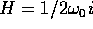 . Allora la soluzione particolare è
. Allora la soluzione particolare è
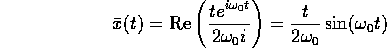
e la soluzione generale dell'equazione a coefficienti reali è
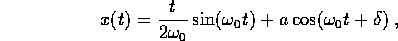
con a, 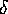 costanti da
determinare con le condizioni iniziali.
costanti da
determinare con le condizioni iniziali.
Tale soluzione può essere confrontata con quella non risonante
(corrispondente al caso 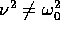 ) osservando che la fase di
) osservando che la fase di
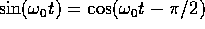 è
è 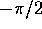 (per
(per
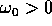 ), quindi intermedia tra i due valori limite che si
ottengono per
), quindi intermedia tra i due valori limite che si
ottengono per 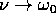 da destra e da sinistra, cioè 0 e
da destra e da sinistra, cioè 0 e
 , mentre l'ampiezza
, mentre l'ampiezza 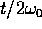 dell'oscillazione forzata
cresce con il tempo. Nella Figura 8.5 si rappresenta la
sola soluzione forzata (a=0).
dell'oscillazione forzata
cresce con il tempo. Nella Figura 8.5 si rappresenta la
sola soluzione forzata (a=0).
In termini euristici, la risonanza può essere descritta come un caso in cui
l'ampiezza cresce per un indefinito accumularsi degli effetti nel
tempo. Dal caso con dissipazione si passa al limite per 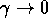 :
se
:
se 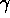 è piccolo l'ampiezza della risposta è
è piccolo l'ampiezza della risposta è 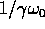 per
per 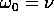 , con fase
, con fase 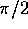 ; il battimento tra
; il battimento tra 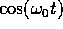 e
e 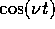 per
per 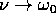 ha periodo che tende
all'infinito, cioè il periodo di accumulazione dell'effetto è
sempre più lungo.
ha periodo che tende
all'infinito, cioè il periodo di accumulazione dell'effetto è
sempre più lungo.