Sommario Tutti sistemi di equazioni differenziali possono essere rese autonome, cioè indipendenti dal tempo, pur di considerare il tempo una variabile dinamica addizionale. Quando però la dipendenza dalle variabili dinamiche è lineare, mentre quella dal tempo e nonlineare, la linearità è una proprietà troppo utile nello studio delle soluzioni per rinunciarvi.
La teoria qualitativa esposta fino a questo punto consente di studiare sistemi dinamici invariabili nel tempo. In teoria, un sistema non autonomo , cioè con secondi membri dipendenti anche dal tempo:
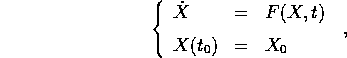
con 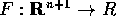 può essere ridotto, per
omogeneizzazione delle variabili, ad un sistema autonomo di
dimensione superiore, ponendo
può essere ridotto, per
omogeneizzazione delle variabili, ad un sistema autonomo di
dimensione superiore, ponendo
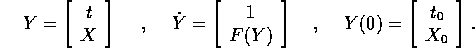
Questo procedimento consente di ricondursi al caso già noto
dei sistemi dinamici, e quindi di applicare a questo caso
risultati importanti come il teorema di esistenza ed unicità
delle soluzioni.
Tuttavia, dal punto di vista del calcolo e dello studio delle
soluzioni, la omogeneizzazione non porta ad alcun vantaggio, visto che
la complessità di un sistema dinamico dipende dalla dimensione.
Inoltre trattare il tempo t come le altre variabili può far
perdere proprietà importanti.
Per esempio, se un sistema è lineare rispetto alle variabili 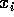 ,
ma nonlineare rispetto alla variabile tempo, ridursi ad un sistema
indipendente dal tempo fa perdere la proprietà di
linearità.
,
ma nonlineare rispetto alla variabile tempo, ridursi ad un sistema
indipendente dal tempo fa perdere la proprietà di
linearità.
Definizione:

con 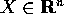 ,
il flusso integrale del sistema non autonomo è
la famiglia a due parametri
,
il flusso integrale del sistema non autonomo è
la famiglia a due parametri 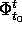 di applicazioni
di applicazioni
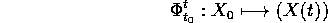
che per ogni tempo 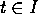 mandano la condizione iniziale
mandano la condizione iniziale
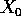 al tempo
al tempo 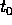 nel valore della corrispondente soluzione al
tempo t.
nel valore della corrispondente soluzione al
tempo t.
La definizione può essere estesa al caso di sistemi
qualunque (non necessariamente lineari): in genere non è
però assicurata l'esistenza di un unico I per ogni 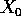 ;
per il teorema di
esistenza e unicità ,
;
per il teorema di
esistenza e unicità ,
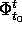 potrà essere definito per
potrà essere definito per 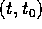 in un
aperto di
in un
aperto di 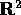 come applicazione tra sottoinsiemi aperti
dello spazio delle fasi
come applicazione tra sottoinsiemi aperti
dello spazio delle fasi 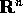 .
.
Per l'unicità della soluzione passante per un punto ad un
tempo dato, se la soluzione con condizione iniziale 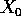 è
definita anche per
è
definita anche per 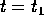 e
e 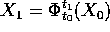 , la
soluzione
, la
soluzione 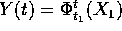 che passa per
che passa per 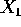 al
tempo
al
tempo 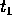 coincide con quella che passa per
coincide con quella che passa per 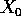 al tempo
al tempo
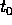 , cioè
, cioè 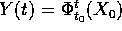 . In altri termini vale la
proprietà:
. In altri termini vale la
proprietà:

In particolare, 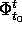 è invertibile e
è invertibile e 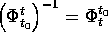 .
.
Se valgono anche delle proprietà di linearità del secondo membro delle equazioni differenziali, l'omogeneizzazione non aiuta nello studio delle soluzioni. Conviene invece sfruttare al massimo le proprietà di linearità del flusso integrale, che conseguono dalla linearità del secondo membro rispetto alle variabili spaziali.
Proprietà:

allora il flusso integrale è una famiglia
a due parametri di applicazioni lineari, cioè esistono
delle matrici 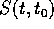 tali che
tali che
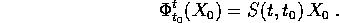
Infatti se 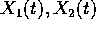 sono due soluzioni e
sono due soluzioni e 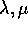 due costanti,
due costanti, 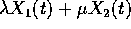 è una soluzione,
con condizioni iniziali combinazione lineare delle
è una soluzione,
con condizioni iniziali combinazione lineare delle
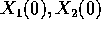 . Dunque l'applicazione
. Dunque l'applicazione 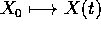 è lineare ed è rappresentata da una matrice (in una base
assegnata).
è lineare ed è rappresentata da una matrice (in una base
assegnata).
Nel seguito 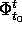 potrà anche indicare - secondo il contesto -
una matrice
potrà anche indicare - secondo il contesto -
una matrice 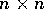 che rappresenta l'operatore lineare stesso,
ovvero potranno coesistere le notazioni
che rappresenta l'operatore lineare stesso,
ovvero potranno coesistere le notazioni
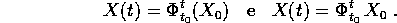
L'insieme di tutte le soluzioni di un sistema lineare omogeneo è quindi uno spazio vettoriale isomorfo allo spazio delle condizioni iniziali, quindi di dimensione n.
Ha quindi senso la definizione di un sistema fondamentale di soluzioni
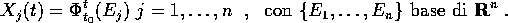
Le soluzioni del sistema sono combinazioni lineari degli elementi di un sistema fondamentale di soluzioni.
Proprietà:
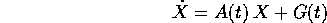
allora il flusso integrale potrà essere espresso come somma
del flusso integrale del corrispondente problema omogeneo
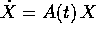 con una soluzione particolare
con una soluzione particolare 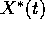 del sistema non
omogeneo:
del sistema non
omogeneo:
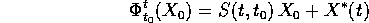
e inoltre la condizione iniziale soddisfatta da 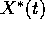 è
è 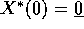 .
.
Questo segue semplicemente dal fatto che se 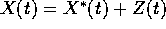 dove
dove 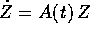 , allora anche X(t) soddisfa
all'equazione non omogenea, ed ha condizione iniziale Z(0).
, allora anche X(t) soddisfa
all'equazione non omogenea, ed ha condizione iniziale Z(0).
L'insieme di tutte le soluzioni di un sistema lineare non omogeneo è quindi uno spazio affine , somma di un sottospazio vettoriale di funzioni (di dimensione n) con una funzione non appartenente ad esso.
Queste due proprietà elementari delle soluzioni di sistemi ed equazioni lineari non autonome sono alla base di tutta la discussione di questo capitolo.