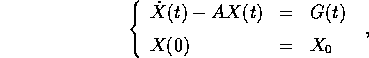
Sommario Le soluzioni di un sistema dinamico lineare omogeneo formano uno spazio vettoriale; quindi le soluzioni di un sistema dinamico lineare non omogeneo si ottengono sommando le soluzioni del sistema omogeneo ad una soluzione particolare . Per un generico secondo membro, la soluzione particolare si può ottenere applicando il metodo della variazione delle costanti arbitrarie: i laboriosi calcoli possono essere evitati se il secondo membro è dello stesso "tipo" delle soluzioni del sistema omogeneo (prodotti di polinomi, esponenziali, seni e coseni), o più precisamente se le sue componenti sono quasipolinomi .
Perturbando un sistema dinamico lineare omogeneo con un termine "forzante" G(t)
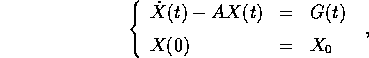
si ottengono soluzioni dell'equazione ``perturbando'' le costanti,
funzione della condizione iniziale, che compaiono nelle soluzioni del
corrispondente sistema omogeneo (da cui forse il nome di
variazione delle costanti arbitrarie ): affinché la funzione
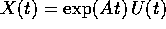, con 
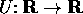e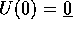 
,
risolva il problema:
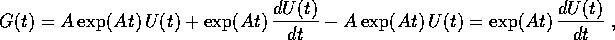
ovvero
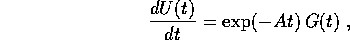
e integrando
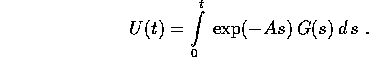
La soluzione generale del sistema è dunque del tipo
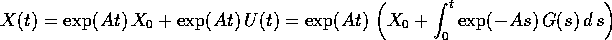
L'integrale contenuto nella formula qui sopra è ben definito per ogni secondo membro G(t) che sia almeno continuo. In pratica però il calcolo della primitiva può essere impossibile per via analitica, e può essere complicato anche per problemi molto semplici. Di conseguenza il metodo della variazione delle costanti arbitrarie è molto efficace come dimostrazione di esistenza delle soluzioni, ma non è necessariamente sempre raccomandabile come procedimento di calcolo esplicito delle soluzioni.
Esempio:
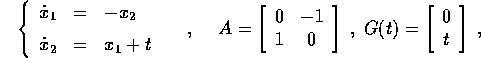
si calcola come al solito
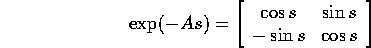
e quindi applicando la formula della variazione delle costanti arbitrarie:
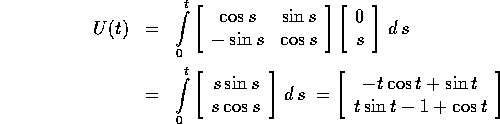
dove l'ultimo passaggio è un integrazione per parti. Allora la
soluzione generale si esprime, in funzione della condizione iniziale
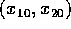, come
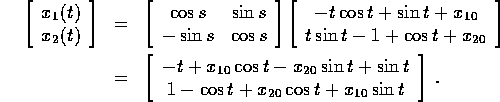
Quando le componenti di G(t) sono quasipolinomi, si può direttamente cercare una soluzione particolare del sistema non omogeneo con componenti combinazioni di quasipolinomi :
Teorema del sistema non omogeneo quasipolinomiale : Se
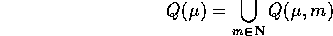
è lo spazio di tutti i quasipolinomi di esponente 
e grado
qualsiasi, sia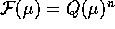 
lo spazio delle
funzioni da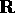 
in 
con componenti quasipolinomiali. Allora,
per ogni matrice A, e per ogni , lo spazio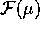 
è
mandato su se stesso dall'operatore (D-A):
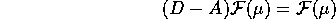
Dimostrazione:
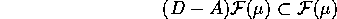
Se le componenti di X sono
in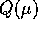 
, lo sono immediatamente anche quelle di 
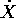e AX.
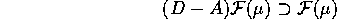
Se le componenti di G(t)
sono in 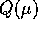, possiamo trovare un Y tale che
(D-A)Y=G usando la variazione delle costanti arbitrarie :
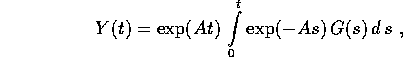
e sono quasipolinomiali i coefficienti di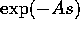 
, le componenti
di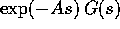 
ed infine quelle di
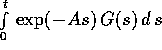, che sono combinazioni lineari
di integrali di quasipolinomi: questi ultimi sono a loro volta
combinazioni lineari di quasipolinomi (come si può vedere integrando
per parti).
Il punto critico della dimostrazione è quindi far vedere che la
soluzione Y ottenuta per variazione delle costanti arbitrarie
contiene soltanto l'esponente che appare nel secondo membro.
Questo sarebbe ovvio se la matrice A fosse della forma
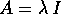; infatti:
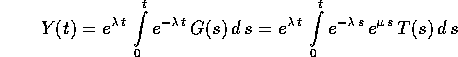
dove T(s) è un vettore di polinomi; perciò, usando il
teorema della derivazione sui quasipolinomi , la primitiva
è un quasipolinomio di esponente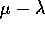 
:
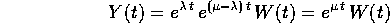
con W(t) a componenti polinomiali, il che è la tesi.
Supponiamo ora che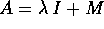 
con M nilpotente; allora:
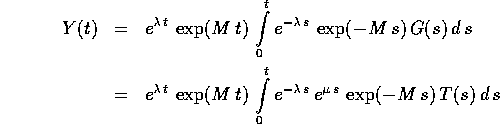
dove T(s) è un vettore di polinomi, e ci si ritrova nello stesso caso
precedente pur di considerare che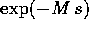 
è una matrice i cui
coefficienti sono polinomi, poiché M è nilpotente.
Quindi
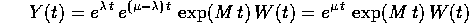
dove W(t) è un vettore di polinomi,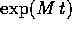 
è una matrice
di polinomi, e quindi Y(t) sta in .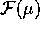
Per completare la dimostrazione basta osservare che il sistema
di equazioni (D-A)Y=G può essere risolto passando ad un sistema
di riferimento in cui A è in forma canonica di Jordan ,
per cui appare come diagonale a blocchi. Ciascuno dei blocchi è del tipo
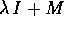, con 
un autovalore di A ed M un
nilpotente. Il ragionamento qui sopra si può quindi ripetere in ogni
autospazio generalizzato di A, ed in ciascuno di questi l'autovalore
scompare dalla soluzione perché si cancella nella
moltiplicazione finale per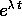 
.
In effetti se non è un autovalore di A, l'operatore
D-A é un isomorfismo su 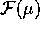, in quanto il suo nucleo
si riduce alla funzione zero (cioè il sistema omogeneo non ha
soluzioni non banali in 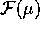) per cui le soluzioni del
sistema con componenti del secondo membro in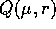 
hanno
componenti in 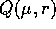senza bisogno di alzare il grado del
polinomio. Da questa semplice considerazione segue la
regola dell'elettrotecnico usata negli esempi che seguono.
I circuiti elettrici danno luogo a sistemi di equazioni differenziali, che sono lineari per circuiti con componenti semplici, e non omogenee in presenza di generatori. Non discutiamo qui la costruzione del modello matematico, ma soltanto svolgiamo un esempio relativamente semplice.
Nel caso di un sistema
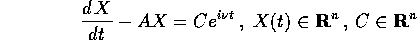
dove A è una matrice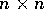 
,
si cerca una soluzione particolare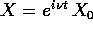 
purché 
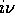non sia una radice del polinomio caratteristico di A. Allora
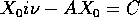cioè
che ha soluzione poiché
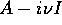è invertibile. Questa regola dell'elettrotecnico
è normalmente usata senza troppe verifiche, in quanto i circuiti
senza generatore hanno soluzioni smorzate, cioè hanno autovalori con parte
reale negativa.
Consideriamo il circuito di un trasformatore : è costituito da due circuiti semplici, uno con un generatore, accoppiati da una mutua induttanza. Le equazioni differenziali sono:
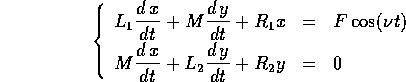
dove i coefficienti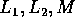 
(per ragioni che vengono spiegate nel corso di Fisica II) sono tali che:
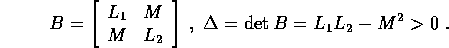
da cui, risolvendo rispetto alle derivate
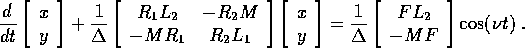
Usando la regola dell'elettrotecnico si provano direttamente soluzioni complesse del tipo
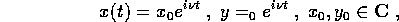
per considerarne poi la parte reale: allora
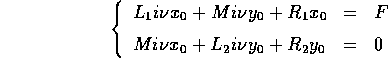
e risolvendo rispetto alle costanti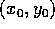 
:
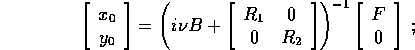
il determinante della matrice da invertire è:
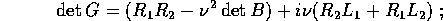
quindi la soluzione è
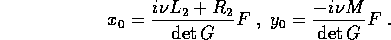
Per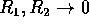 
si ottengono oscillazioni con ampiezze:
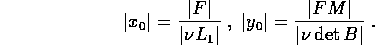
Nel caso in cui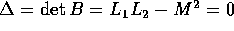 
, 
, 
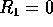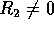si ha il
trasformatore perfetto:
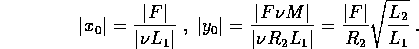
Esercizio
Verificare che per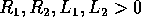 
la matrice
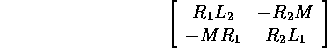
ha autovalori con parte reale negativa, quindi è legittimo usare la regola dell'elettrotecnico. (Soluzione)