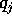 .
Se
.
Se 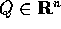 , si considerano
, si considerano 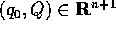 ,
con
,
con 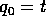 , ed un momento addizionale
, ed un momento addizionale
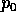 .
.
Sommario Con lo stesso formalismo descritto fin qui, ma con formule e regole di calcolo modificate, si possono trattare sistemi lagrangiani o hamiltoniani in cui vi sia una esplicita dipendenza dal tempo In particolare, i cambiamenti di coordinate che dipendono dal tempo possono trasformare hamiltoniane e lagrangiane indipendenti dal tempo in altre che ne dipendono, o viceversa. Le regole da applicare ai casi dipendenti dal tempo possono essere ricavate per omogeneizzazione, cioè trattando il tempo come una variabile come le altre che parametrizzano lo spazio delle configurazioni.
Dato un sistema hamiltoniano definito da una funzione di
Hamilton dipendente dal tempo H=H(t,Q,P), è sempre semplice
ricondursi al caso indipendente
dal tempo mediante omogeneizzazione , cioè trattando il
tempo t come se fosse una delle coordinate 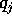 .
Se
.
Se 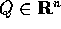 , si considerano
, si considerano 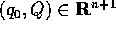 ,
con
,
con 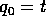 , ed un momento addizionale
, ed un momento addizionale
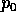 .
.
Per ottenere equazioni di Hamilton che siano equivalenti a quelle originali, si aggiunge a
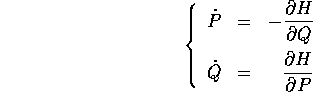
un'equazione del tempo 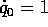 . Basta cioè
considerare una hamiltoniana omogenea
. Basta cioè
considerare una hamiltoniana omogenea
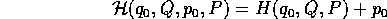
che dà luogo ad equazioni di Hamilton corrispondenti a quelle precedenti, più
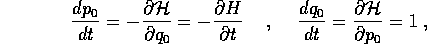
di cui la seconda è l'equazione del tempo, con soluzione
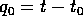 (la costante
(la costante 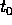 si può anche porre
uguale a zero). La prima equazione mostra che
si può anche porre
uguale a zero). La prima equazione mostra che
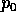 è legata al valore della hamiltoniana:
è legata al valore della hamiltoniana:
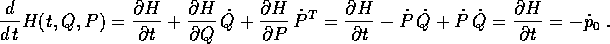
Quindi vale la relazione
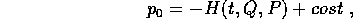
dove si può sempre scegliere la costante uguale a zero, e
quindi scegliere di considerare solo le soluzioni con
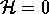 .
.
Una trasformazione canonica dipendente dal tempo può essere definita implicitamente da una funzione generatrice dipendente dal tempo :
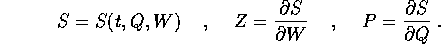
Questa formula è ottenuta da una funzione generatrice omogenea
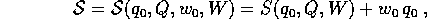
che è costruita in modo tale che la trasformazione
della variabile tempo 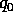 sia
sia
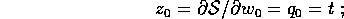
il tempo non viene cambiato. Cambia però la hamiltoniana, poiché
la variabile 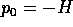 viene trasformata da
viene trasformata da
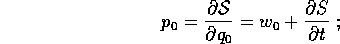
la nuova hamiltoniana 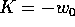 , che definisce la dinamica nello
spazio delle (W,Z), è perciò
, che definisce la dinamica nello
spazio delle (W,Z), è perciò
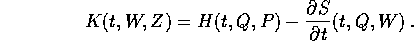
Lo stesso formalismo omogeneo può anche essere impiegato per cambiare variabile indipendente: per esempio
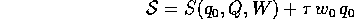
definisce il cambiamento di scala dei tempi di un fattore 
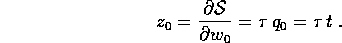
Ad esso è associato un cambiamento di scala della hamiltoniana
di 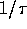 :
:
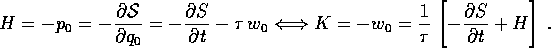
Consideriamo per esempio un cambiamento di coordinate nello
spazio 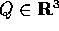 dato da una rotazione
con velocità angolare fissa
dato da una rotazione
con velocità angolare fissa 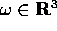 :
:

Calcoliamo la trasformazione canonica che estende questo cambiamento di coordinate allo spazio delle fasi, usando la funzione generatrice dipendente dal tempo
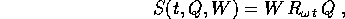
e troviamo che la prima equazione 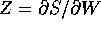 coincide con la rotazione definita sopra; inoltre
coincide con la rotazione definita sopra; inoltre
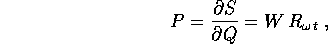
e poiché 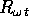 è ortogonale
si trova che le P vengono ruotate dello stesso angolo.
è ortogonale
si trova che le P vengono ruotate dello stesso angolo.
Però la nuova hamiltoniana contiene un termine supplementare che proviene dalla derivata rispetto al tempo della funzione generatrice, calcolabile con l'ausilio della regola della velocità angolare :
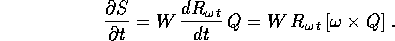
Considerando che il prodotto vettore viene conservato dalle rotazioni e che il vettore velocità angolare è invariante per la rotazione, si ottiene
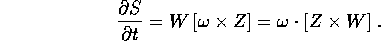
Se H è la funzione di Hamilton nelle (P,Q), la dinamica nelle (W,Z) sarà data dalla nuova funzione di Hamilton
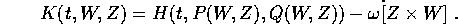
Le nuove equazioni di Hamilton conterranno due parti: una proveniente dalla rotazione dei secondi membri delle equazioni originali, l'altra proveniente dalla derivata del prodotto triplo
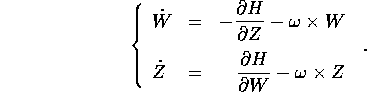
Esempio:
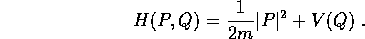
Passando in coordinate rotanti con velocità angolare
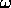 la hamiltoniana è
la hamiltoniana è
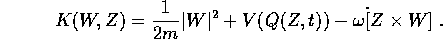
Si noti che la nuova hamiltoniana non è l'energia, dalla quale
differisce per il prodotto scalare della velocità angolare
 per il momento angolare del corpo puntiforme.
Le equazioni di Hamilton diventano
per il momento angolare del corpo puntiforme.
Le equazioni di Hamilton diventano
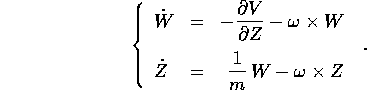
Ricaviamo le equazioni di moto (in effetti le equazioni di Lagrange) nel sistema rotante (W,Z): per la trasformata di Legendre inversa si ha
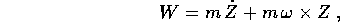
derivando i momenti si ottiene
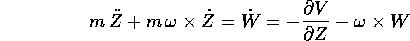
e, sostituendo,
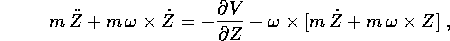
ossia
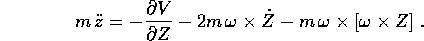
I due termini supplementari sono la forza apparente di Coriolis
e la forza apparente centrifuga , che compaiono nell'espressione
dell'accelerazione 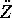 nel sistema rotante, ma non corrispondono
ad alcuna forza nel sistema inerziale.
nel sistema rotante, ma non corrispondono
ad alcuna forza nel sistema inerziale.