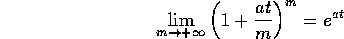
Sommario Il più semplice procedimento per approssimare un sistema dinamico continuo con uno discreto è quello di Eulero. Le soluzioni del sistema discreto così ottenuto approssimano le soluzioni del sistema continuo, in un senso che può essere reso rigoroso con la nozione di convergenza uniforme. La differenza tra le due, cioè l'errore di discretizzazione, è una funzione rapidamente crescente con il passo, per cui la potenza di calcolo richiesta per ottenere soluzioni accurate è notevole.
Come è noto, una definizione alternativa della funzione esponenziale di variabile reale è:
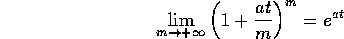
L'analogo matriciale è già stato esaminato come
Problema 2.2: se A è una matrice quadrata
:
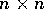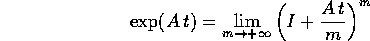
per ogni t in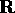 
. Ripetendo l'argomento della soluzione
del problema, si trova (sostituendo 
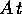al posto di A) la
maggiorazione
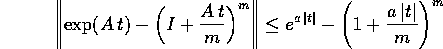
Nel caso scalare la successione converge uniformemente sull'intervallo [-t,t], con t arbitrario (ma fissato). Ma allora, utilizzando il teorema della convergenza in norma , anche la definizione alternativa di esponenziale nel caso matriciale converge uniformemente su [-t,t]. Da questo segue (per la proprietà (2.4) della norma uniforme ) che
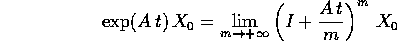
uniformemente per t in ogni intervallo limitato. L'aspetto
interessante di questa formula è che al primo membro abbiamo il
flusso integrale di un sistema dinamico continuo lineare; a secondo
membro sotto segno di limite abbiamo l'analoga rappresentazione di tutte le
soluzioni (in funzione della condizione iniziale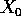 
) di un
sistema dinamico discreto lineare, e precisamente
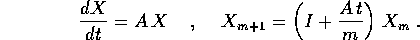
La relazione tra il sistema dinamico continuo e quello discreto
ottenuta qua sopra è un caso particolare (lineare) del
metodo di Eulero . La motivazione geometrica
dell'approssimazione di Eulero può essere apprezzata dalla
Figura 4.3. Se si deve calcolare la soluzione con
condizione iniziale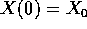 
al tempo 
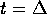, si suddivide
l'intervallo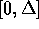 
in cui varia t in m sottointervalli,
ciascuno di lunghezza pari al passo d'integrazione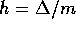 
,
con m abbastanza
grande. Allora si approssima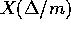 
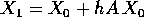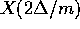con 
,
con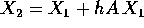 
, eccetera, ad ogni passo
rimpiazzando la vera soluzione con la sua approssimazione lineare
(cioè con il suo differenziale).
Benché nel sistema dinamico discreto appaiano solo i punti che
approssimano la soluzione ai tempi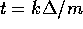 
con k intero, si
può immaginare di descrivere un'approssimazione per tutti i tempi
usando l'interpolazione lineare (cioè ancora lo
stesso differenziale) per i punti intermedi. Il
poligono di Eulero ottenuto congiungendo
i punti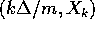 
è il grafico
di una funzione di t che è continua ma non differenziabile, e che
approssima la soluzione nel senso che la successione di poligoni di
Eulero ottenuti per m crescente tende alla soluzione del sistema
dinamico continuo, uniformemente su .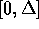
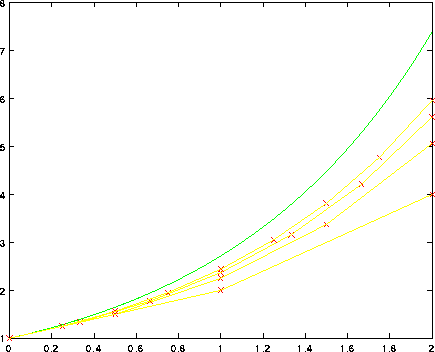
Figure 4.3: Il poligono di Eulero: ad ogni passo temporale
si approssima la soluzione del sistema dinamico continuo con il suo
differenziale nel punto precedentemente calcolato; in questo esempio
la soluzione dell'equazione y'=y è approssimata con il metodo di
Eulero usando 2,4,6 ed 8 passi.
L'errore di troncamento locale commesso in un passo di lunghezza h>0 del metodo di Eulero al posto della soluzione esatta si può maggiorare usando il confronto in norma con l'esponenziale:
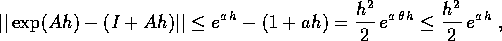
dove a=||A|| e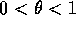 
; il penultimo passaggio è il resto di
Lagrange della formula di Taylor per la funzione esponenziale di
variabile reale.
Al contrario l'errore di troncamento accumulato usando m passi del metodo di Eulero per arrivare a t=mh non si calcola così\ facilmente, e converrà utilizzare una formula generale che risulta dal teorema di convergenza del metodo di Eulero .
Esempio:
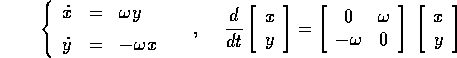
Il metodo di Eulero dà il sistema dinamico discreto:
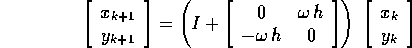
La soluzione del sistema discreto contiene le potenze della matrice
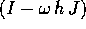, e quindi si scrive più facilmente
interpretando questa matrice come numero complesso, e poi usando la
rappresentazione mediante modulo e argomento:
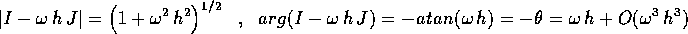
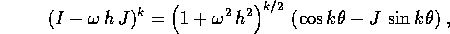
In conclusione la matrice che esprime la soluzione al passo k in funzione delle condizioni iniziali è una dilatazione di un fattore
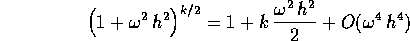
che non è molto diverso da uno per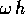 
piccolo, seguita da
una rotazione di un angolo
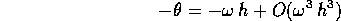
che differisce di poco dalla rotazione di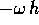 
della
soluzione del sistema continuo, sempre per 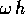piccolo.
Supponiamo di dover approssimare la soluzione di un sistema dinamico
nonlineare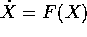 
con condizione iniziale .
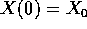Il metodo di Eulero consiste nell'approssimare la soluzione al tempo
h con l'approssimazione lineare:
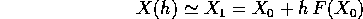
La soluzione a tempi successivi può essere approssimata ripetendo il procedimento, cioè con la successione definita per ricorrenza:
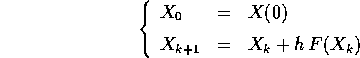
Se si desidera avere delle informazioni sui valori assunti da X(t) per valori di t intermedi tra kh e (k+1)h si può ricorrere ad un'interpolazione, per esempio lineare ottenendo ancora il poligono di Eulero . L'errore di troncamento locale è sempre infinitesimo del secondo ordine rispetto ad h, il che si può descrivere simbolicamente con la formula:
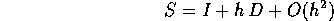
L'errore di troncamento accumulato è la differenza tra la successione definita per ricorrenza dal metodo di Eulero e la soluzione del sistema dinamico con le stesse condizioni iniziali:
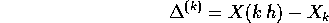
Teorema della convergenza del metodo di Eulero : Se il campo vettoriale F(X) è lipschitziano di costante L e limitato in modulo dalla costante M, cioè se
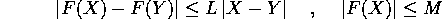
per ogni X,Y in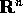 
, allora l'errore accumulato 
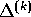dopo il tempo 
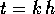soddisfa alla diseguaglianza
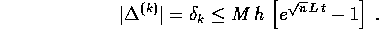
Dimostrazione:
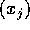ed il campo vettoriale F(X)
ha componenti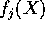 
, con j=1, n, la soluzione al
passo k+1 si può calcolare con la formula di Lagrange:
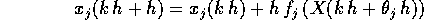
dove per ogni j va scelto u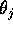n 
con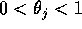 
. Si noti che
ciascuno dei punti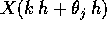 
non può distare da 
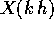più di 
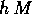, sempre per la formula di Lagrange.
Allora l'errore di troncamento accumulato si accresce secondo la formula:
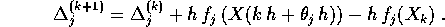
Se si passa ai valori assoluti, usando la diseguaglianza triangolare e tenendo conto che la differenza,nella formula precedente, tra i valori di F calcolati in due punti diversi si può maggiorare con L volte la norma della differenza degli argomenti, si ottiene
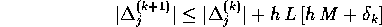
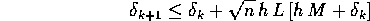
Definiamo un'altra successione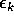 
che sia soluzione della
stessa equazione ma con il segno di uguaglianza, e con
:
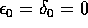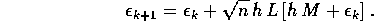
Allora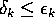 
, ma la successione 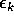è
soluzione di un'equazione alle differenze finite lineare
non omogenea , e si può calcolare
esplicitamente
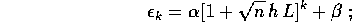
la costante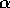 
si ricava per sostituzione:
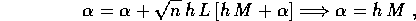
e imponendo la condizione iniziale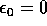 
si trova 
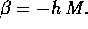In conclusione
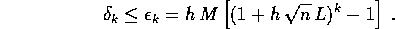
Per ottenere la tesi basta sostituire 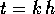ed usare la diseguaglianza
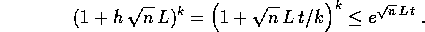
Il fattore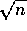 
appare perché si sono usate nella
dimostrazione due norme, quella euclidea nel maggiorare la lunghezza
degli spostamenti, e quella di matrice che è contenuta nella
relazione tra matrice jacobiana e costante di Lipschitz.
La maggiorazione per l'errore di troncamento accumulato che si ricava in generale, cioè per ogni possibile sistema dinamico, si rivela pessimistica in casi specifici. Tuttavia che l'accumulazione dell'errore possa essere esponenziale è inevitabile; in molti casi l'esponente sarà più piccolo della costante di Lipschitz, e sarà piuttosto legato all'esponente di Lyapounov della soluzione che si cerca di approssimare.