Sommario Un sistema alle differenze finite lineari si risolve calcolando le potenze di una matrice; questo calcolo diventa molto più semplice se la matrice è ridotta alla forma canonica di Jordan. Modelli alle differenze finite lineari sono impiegati in molti campi; qui diamo degli esempi tratti dalla modellizzazione di fenomeni economici.
Un sistema dinamico discreto lineare in 
è
della forma:
dove A è una matrice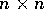 
invertibile ed 
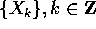è l'orbita. L'orbita può essere descritta mediante le potenze di
A:
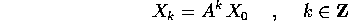
però il calcolo esplicito di una potenza elevata di una matrice richiede un gran numero di operazioni aritmetiche (per di più, questo numero cresce con il cubo della dimensione n).
Si può allora cercare di semplificare questo calcolo mediante un cambiamento di coordinate lineare : se
è la stessa orbita vista in un nuovo sistema di coordinate,
associate alla base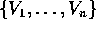 
mediante la matrice V con
colonne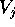 
(si ricorda che in tal caso B è invertibile, e
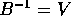), allora
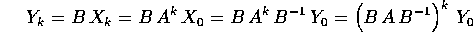
Quindi nel nuovo sistema di coordinate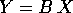 
il sistema dinamico
discreto ha per matrice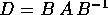 
e per soluzione
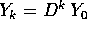; se la nuova base è scelta in modo che il calcolo
delle potenze di D sia più semplice, allora converrà esprimere
la soluzione passando attraverso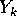 
, cioè:
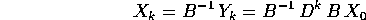
Per esempio, se la matrice A è diagonalizzabile , allora
possiamo scegliere la nuova base in modo che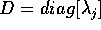 
, dove
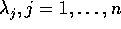sono gli autovalori di A (che sono
tutti reali). Allora la soluzione nello spazio delle coordinate Y
sarà semplicemente
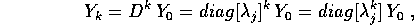
e, tornando alle coordinate X,
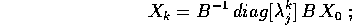
ogni coordinata di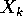 
è quindi una combinazione lineare, a
coefficienti dipendenti dalla condizione iniziale, dei monomi
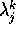formati con gli autovalori di A.
L'analogia con il caso continuo è così stretta che non vale la pena di ripetere tutto lo svolgimento della teoria nel caso di autovalori coniugati , nel caso di una matrice semisemplice e nel caso nilpotente ; si può passare direttamente al risultato generale.
Per il teorema della decomposizione S + N la matrice A può comunque essere descritta come somma di una matrice semisemplice S ed una matrice nilpotente N, che commutano tra loro: SN=NS. Allora vale la formula del binomio di Newton :
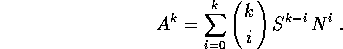
In questo modo il calcolo delle potenze è semplificato, e può essere descritto in ogni caso in termini di polinomi:
Teorema delle soluzioni dell'equazione alle differenze prime :
Per ogni matrice A di tipo 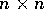, le soluzioni di
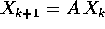hanno componenti che si possono esprimere come
combinazioni lineari delle seguenti successioni:
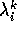, dove 
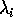è un autovalore reale di A.
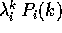, dove 
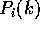è un polinomio di
grado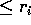 
nella variabile k, e 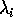è un autovalore
reale di A di molteplicità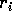 
.
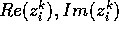, dove 
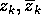è una
coppia di autovalori complessi coniugati di A.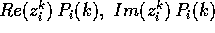
, dove 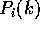è
un polinomio di grado 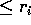nella variabile k, e 
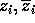è una coppia di autovalori complessi coniugati di A di
molteplicità .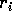
Si noti che i
coefficienti del polinomio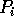 
dipendono da 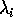. Se si
vuole esprimere la dipendenza da 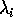, e non da
k, si può usare l'espression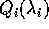e 
dove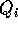 
è
un polinomio di grado k che contiene monomi di grado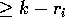 
.
Dimostrazione:
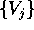sia stata scelta in modo che
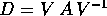sia in forma canonica di Jordan reale :
allora D=S+N con S una matrice che ha sulla diagonale gli
autovalori reali, e per ogni coppia di autovalori complessi
coniugati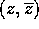 
la matrice 
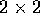che rappresenta z;
la matrice nilpotente N è in questo caso diagonale
a blocchi con blocchi in forma canonica del nilpotente .
Allora esaminiamo l'espressione della soluzione:
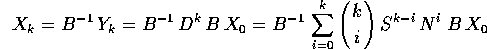
prendendo in considerazione i
blocchi di Jordan che si
riferiscono a ciascuno dei quattro casi (radici reali e complesse,
semplici e multiple). Nel caso di radici semplici appare solo la
potenza k-esima dell'autovalore (inteso come matrice 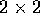nel
caso complesso). Nel caso di radici multiple, la conclusione segue
dall'osservazione che
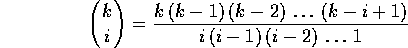
è un polinomio di grado i nella variabile k.
Definizione:
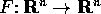è una applicazione stabile
nel punto 
se
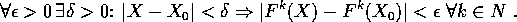
Si dice che 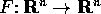è una
applicazione asintoticamente stabile
nel punto se è stabile, ed inoltre
esiste un intorno U di tale che
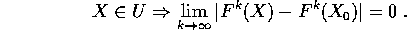
Supponiamo che 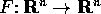sia un'applicazione lineare,
cioè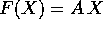 
con A una matrice .
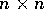Poiché le successioni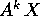 
contengono le potenze k-esime degli
autovalori, la stabilità della soluzione nulla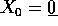 
è controllata dai moltiplicatori di Lyapounov , che sono i
moduli degli autovalori: l'applicazione lineare è asintoticamente
stabile nel punto 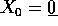se e solo se tutti i
moltiplicatori di Lyapounov sono minori di 1.
Avere tutti i moltiplicatori di Lyapounov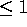 
è
necessario, ma non sufficiente per la stabilità nella soluzione
nulla; infatti in presenza di autovalori multipli di modulo 1
possono essere presenti termini a crescenza polinomiale nell'indice k.
L'analogia con Il teorema del pozzo lineare può essere resa esplicita definendo, in questo caso, gli esponenti di Lyapounov come i logaritmi naturali dei moltiplicatori di Lyapounov, cioè come i numeri reali
per ogni autovalore 
della matrice A del sistema dinamico
discreto lineare.
Questa seconda definizione di esponenti di Lyapounov è
coerente con la precedente, nel senso che segue. Se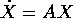 
è un
sistema dinamico continuo lineare, ed i suoi esponenti di Lyapounov
sono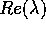 
, con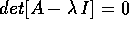 
, allora consideriamo il
sistema dinamico discreto lineare ottenuto per
discretizzazione con passo h:
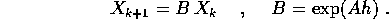
Allora B ha per autovalori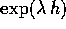 
e per moltiplicatori
di Lyapounov i moduli
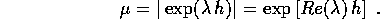
Definizione:
:
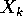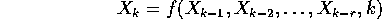
dove f è una funzione assegnata di tutte le sue variabili.
L'equazione alle differenze finite è lineare se la
funzione f è lineare rispetto alle variabili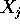 
, ossia se:
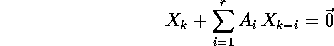
dove le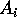 
sono matrici di tipo 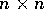se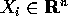 
.
Si noti che le matrici potrebbero anche dipendere
dall'indice k; qui di seguito svolgeremo il caso in cui non c'è
dipendenza da k.
Se le matrici 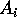non dipendono da k, allora si può trasformare
un'equazione alle differenze finite di ordine r e lineare, definita
su , in un sistema dinamico discreto e lineare definito su
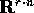, con un procedimento sostanzialmente identico a quello
usato per un'equazione differenziale lineare di ordine
r. Poniamo:
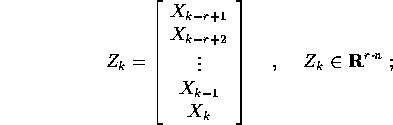
allora esiste una matrice B di tipo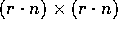 
tale
che il sistema dinamico discreto lineare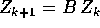 
è del
tutto equivalente all'equazione alle differenze finite di ordine r;
la condizione affinché B sia invertibile è che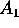 
sia
invertibile.
La possibilità di ricondurre un'equazione alle differenze
finite ad un sistema dinamico discreto non è ristretta al caso
lineare. Se la funzione f che definisce l'equazione alle differenze
finite è differenziabile (di classe almeno 
) rispetto a tutte
le variabili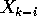 
e non dipende da k, si può procedere nello
stesso modo usato sopra; la condizione di invertibilità è
soddisfatta se la matrice jacobiana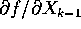 
è
invertibile.
Non è essenziale nemmeno la restrizione che l'equazione alle
differenze finite non dipenda dall'indice. Si può sempre aggiungere
alle variabili dinamiche del sistema una variabile t con l'equazione
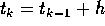; questo trucco è l'analogo discreto della
omogeneizzazione usata nel caso continuo.
Ci limiteremo nel seguito a considerare il caso n=1, cioè per il caso lineare:
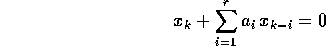
con i coefficienti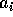 
costanti di 
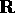, e la sola variabile
dinamica x. Allora, ponendo
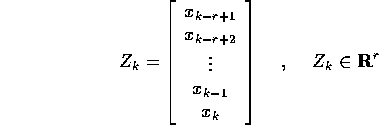
si ottiene il sistema dinamico discreto
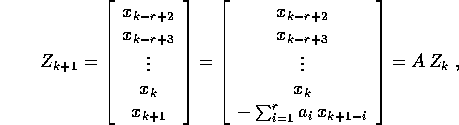
dove la matrice A è data da:
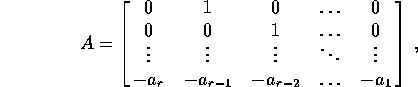
cioè dalla la matrice compagna del polinomio con i
coefficienti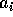
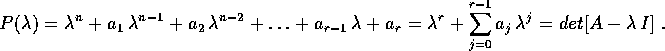
Ne seguono risultati concettualmente identici a quelli del caso dell'equazione differenziale lineare . L'analogia è più evidente se si introduce l'operatore spostamento S:
Allora un'equazione alle
differenze finite lineari si esprime mediante un polinomio
nell'operatore S, tenendo conto che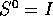 
è l'operatore
identità:
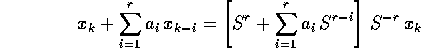
Teorema dell' operatore alle differenze finite lineare :
Il polinomio P ha radice 
se e solo se la progressione
geometrica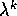 
è una soluzione dell'equazione alle
differenze finite lineari con gli stessi coefficienti:
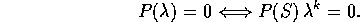
Dimostrazione:
Teorema delle soluzioni dell'equazione alle differenze finite : Ogni soluzione dell'equazione alle differenze finite di ordine r:
è una combinazione lineare delle r successioni seguenti:
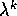per ogni radice reale di P(z)=0.
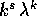con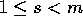 
per ogni radice reale
di molteplicità m.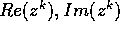
per ogni coppia 
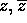di radici complesse coniugate di
P(z)=0.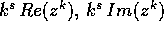
con 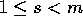per ogni coppia
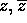di radici complesse coniugate di molteplicità m.
Le soluzioni elencate sono linearmente indipendenti se gli
autovalori sono diversi da zero; in tal caso è possibile trovare una
soluzione per ogni sequenza iniziale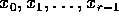 
. Se
invece c'è una radice nulla del polinomio P(z), questo vuol dire
che l'equazione alle differenze finite non è veramente di ordine
r, e la sequenza iniziale deve essere più corta.
Dimostrazione:
Un'equazione alle differenze finite lineari non omogenea , cioè con a secondo membro una successione nota, si trattano secondo lo stesso principio usato nel Capitolo 8 per le equazioni differenziali lineari non omogenee, cioè aggiungendo alle soluzioni dell'equazione omogenea una soluzione particolare dell'equazione non omogenea. Quest'ultima si può trovare tra le funzioni dello stesso tipo del secondo membro, per esempio una costante se il secondo membro è costante.
Esercizio Studiare i seguenti problemi alle differenze finite lineari del secondo ordine:
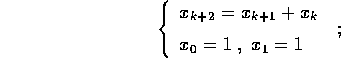
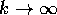, è limitata la soluzione di
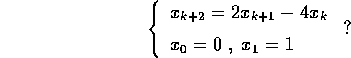
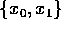il comportamento delle soluzioni
di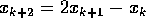 
.
Diamo di seguito alcuni esempi di modelli di fenomeni economici mediante equazioni alle differenze finite lineari. Gli esempi citati sono microeconomici, cioè descrivono la legge della domanda e dell'offerta per un singolo bene su di un dato mercato; esistono però anche modelli alle differenze finite di fenomeni macroeconomici, cioè dell'andamento di un intera economia.
Esempio:
, con tre variabili
(p,s,d) la cui interpretazione è la seguente:
Il tempo è discreto,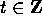 
(come è logico perché i fenomeni
economici non possono essere istantanei).
Le equazioni del modello sono le seguenti:
dove a,b>0 sono costanti assegnate. a è il consumo a prezzo zero, cioè il massimo consumo utile al consumatore, b è l'elasticità della domanda; a/b rappresenta il prezzo massimo (oltre il quale il consumo cessa del tutto).
dove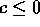 
(se il prezzo è zero, nessuno produce), ed f>0
misura la risposta del produttore all'aumento di prezzo.
per cui domanda ed offerta sono in equilibrio ad ogni momento, senza
ritardi. Ne segue che il modello può in realtà essere
considerato come sistema dinamico discreto in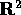 
.
Si può comprendere dall'equazione (2) che l'unità di tempo corrisponde al tempo necessario per la produzione; per esempio può essere un anno per i prodotti agricoli che possono essere seminati e raccolti solo una volta all'anno.
Allora si può ricavare una singola equazione alle differenze finite per la variabile p che rappresenta il prezzo:
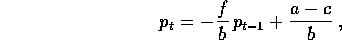
e la seconda variabile (d=s) si può dedurre da (1), oppure da (2),
in funzione di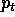 
.
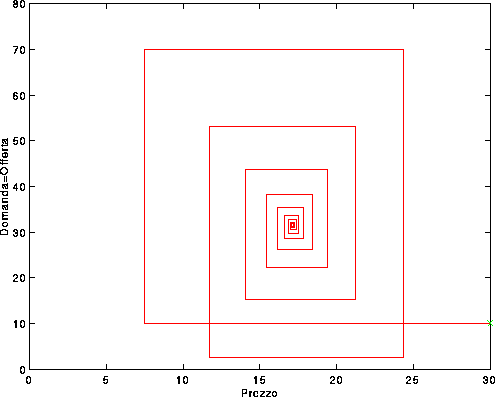
Figure 4.1: Modello della ragnatela: nel caso stabile, la
soluzione converge all'equilibrio. Per ogni passo temporale abbiamo
disegnato prima il cambiamento di prezzo e poi quello dell'offerta che
ne consegue.
L'equazione alle differenze finite per la variabile prezzo è
non omogenea ,
con secondo membro costante; perciò ha una
soluzione di equilibrio, cioè costante,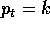 
con
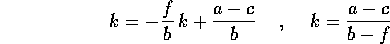
a cui bisogna aggiungere la soluzione generale dell'equazione omogenea:
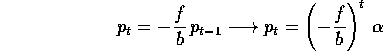
dove la costante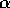 
è arbitraria; si può quindi scegliere
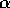in modo da soddisfare alla condizione iniziale 
:
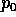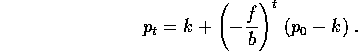
Qualitativamente la soluzione è un'oscillazione (-f/b<0) che è
smorzata se f/b<1, amplificata se f/b>1; nel primo caso la
soluzione tende a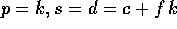 
per 
, seguendo un
percorso che ha l'aspetto di una ragnatela (se si congiunge ogni punto
dell'orbita con il successivo mediante due segmenti paralleli agli
assi, vedi Figura 4.1).
Esempio:
; allora l'equazione (3) è rimpiazzata
da:
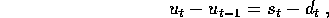
che descrive l'accrescimento delle scorte con l'invenduto.
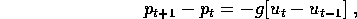
dove la costante g>0 descrive come l'invenduto fa calare il prezzo.
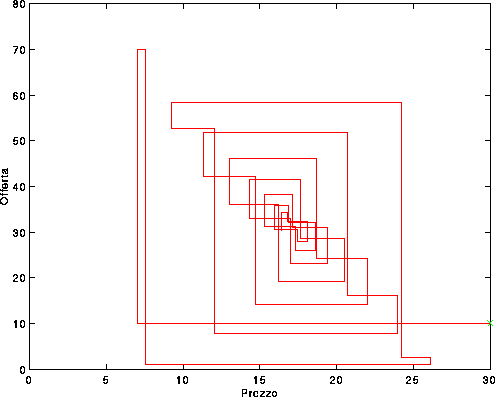
Figure 4.2: Modello delle scorte: con gli stessi valori dei
parametri a,b,c,f della figura precedente, la soluzione converge
all'equilibrio. Poiché però il prodotto fg è appena minore di
uno, prezzi e offerta tendono all'equilibrio in modo più laborioso.
Possiamo sintetizzare le equazioni (1), (2), (4) e (5) in un'unica equazione alle differenze finite di ordine 2 per la variabile prezzo:
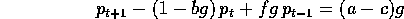
che ha la soluzione particolare costante 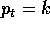data dall'equazione:
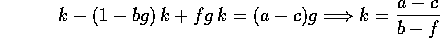
ossia il prezzo di equilibrio è lo stesso del modello della ragnatela; mentre le soluzioni dell'equazione omogenea:
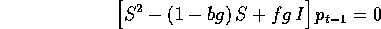
dipendono dalle radici dell'equazione caratteristica della matrice compagna:
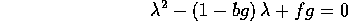
che possono essere reali o complesse, a seconda del segno del
discriminante. La stabilità asintotica del prezzo, cioè la
convergenza per 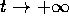al prezzo di equilibrio, è
assicurata soltanto se i moduli di entrambe le radici (cioè i
moltiplicatori di Lyapounov ) sono <1. In ogni caso il
prodotto delle radici è il numero reale fg>0, e se fg>1 la
soluzione di equilibrio è certamente instabile (troppa avidità e
troppa paura!).